 円
円
 円
円
6つの小さい円と大きい円 2024城北高校

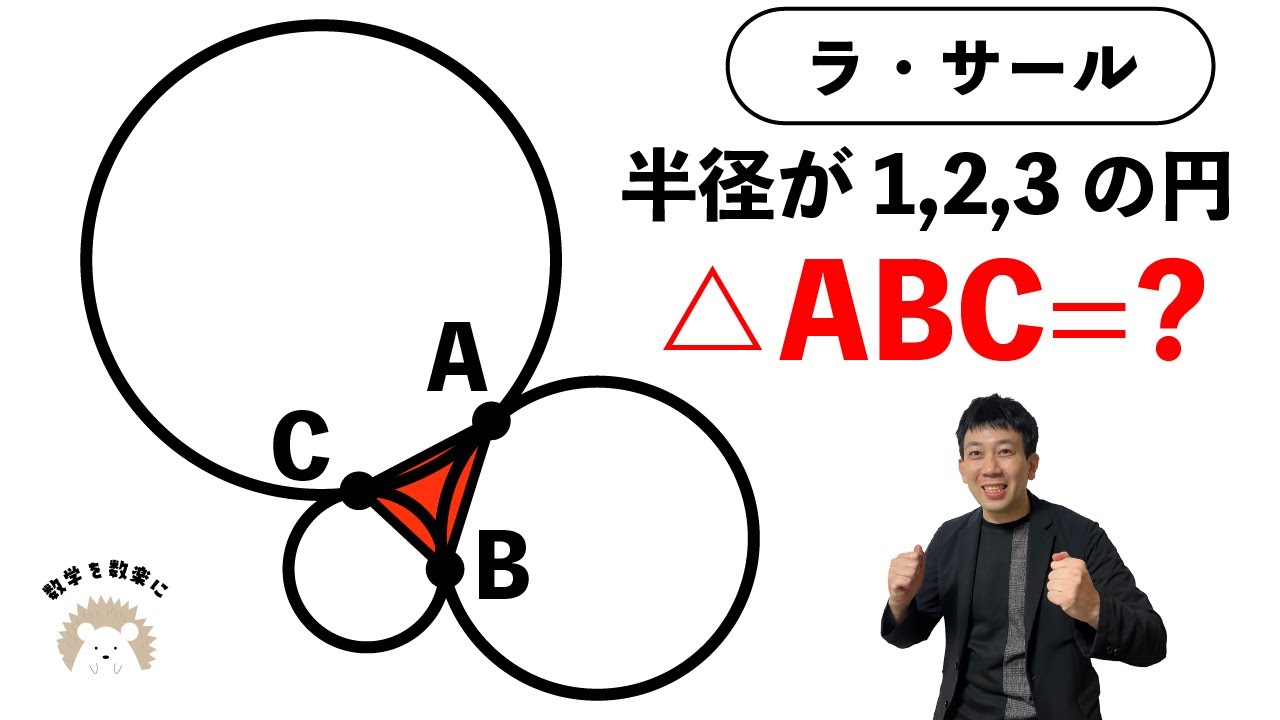
3つの円と三角形の面積 ラ・サール
【その場で導け…!】図形:開智高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#円#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
開智高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
このコンテンツの作成手段
この動画を見る
開智高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
このコンテンツの作成手段
【別解付きで解きたい…!】図形:函館白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#函館白百合学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
函館白百合学園高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
函館白百合学園高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
三角形に内接円?なにこれ?

単元:
#数学(中学生)#中3数学#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角形の外周の長さと内接する円の半径を用いて三角形の面積を求める公式について説明する動画です
この動画を見る
三角形の外周の長さと内接する円の半径を用いて三角形の面積を求める公式について説明する動画です
【中学数学】円周角の定理の問題~2024年度埼玉県公立高校入試大問1(10)~【高校受験】

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#埼玉県高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
この動画を見る
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
【中学数学】円周角の定理の逆~分かりやすく丁寧に~【中3数学】

単元:
#数学(中学生)#中3数学#円
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 図におけるx, yの角度を求めよ
(2) 図におけるx, yの角度を求めよ
※図は動画内参照
この動画を見る
(1) 図におけるx, yの角度を求めよ
(2) 図におけるx, yの角度を求めよ
※図は動画内参照
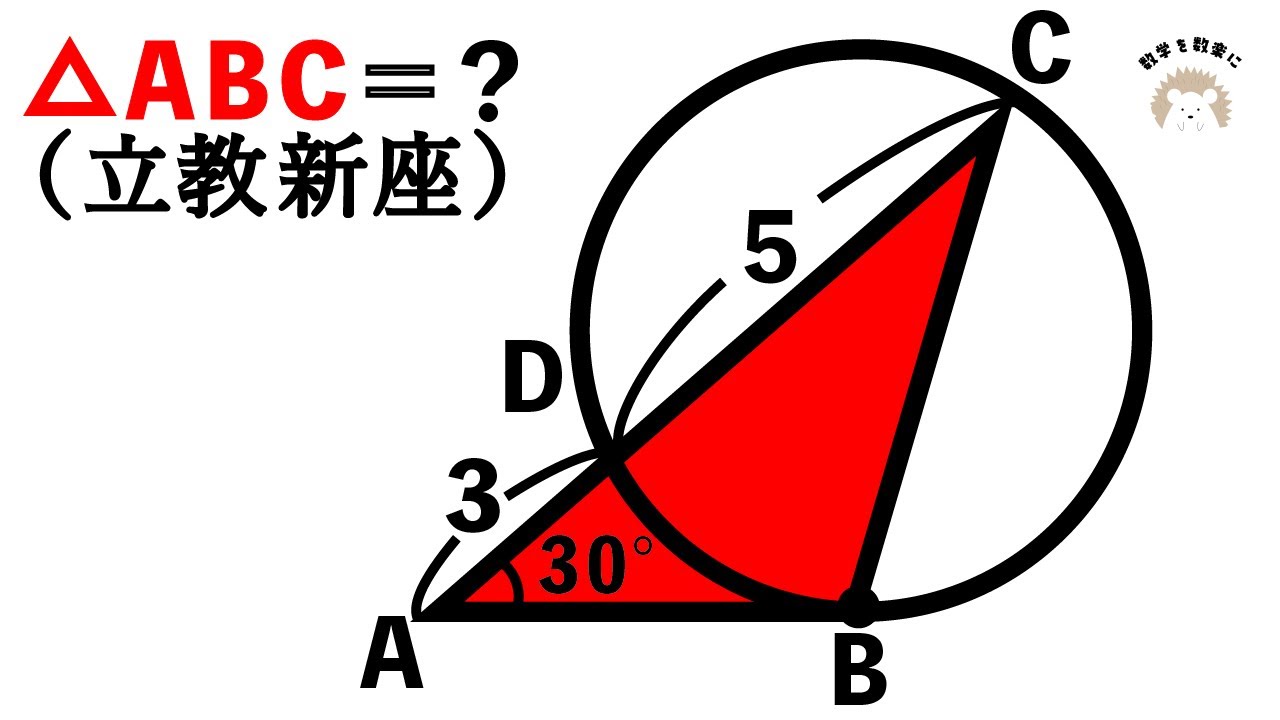
円と接線と三角形 立教新座
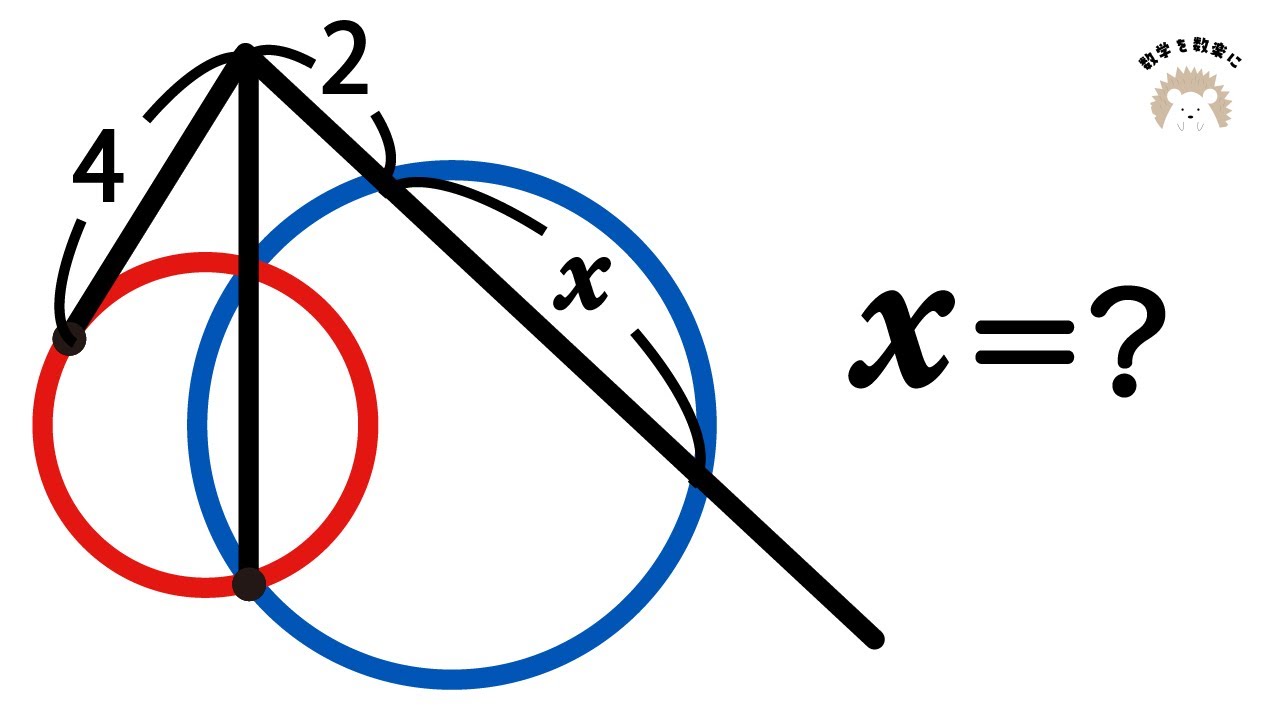
〇〇きの定理で解説!!
よくある円のパターン 〇〇をみつけろ! 灘高校
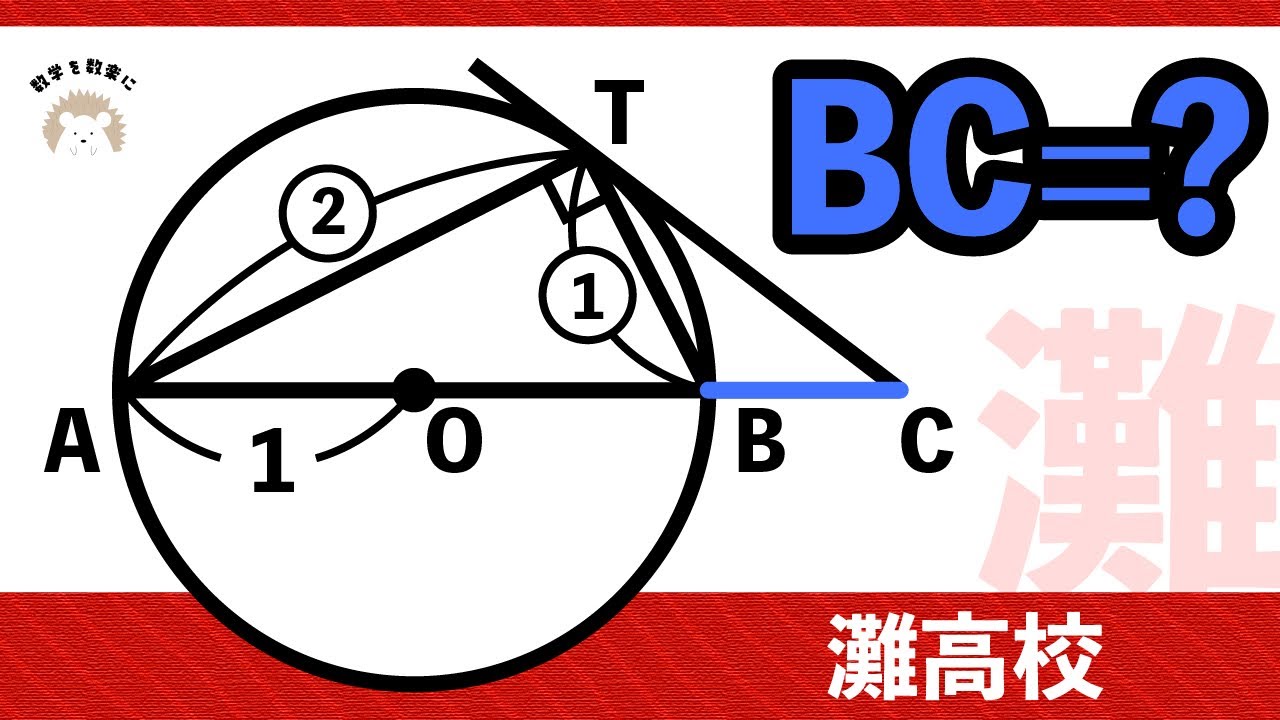
よくある円のパターン 〇〇をみつけろ! 灘高校

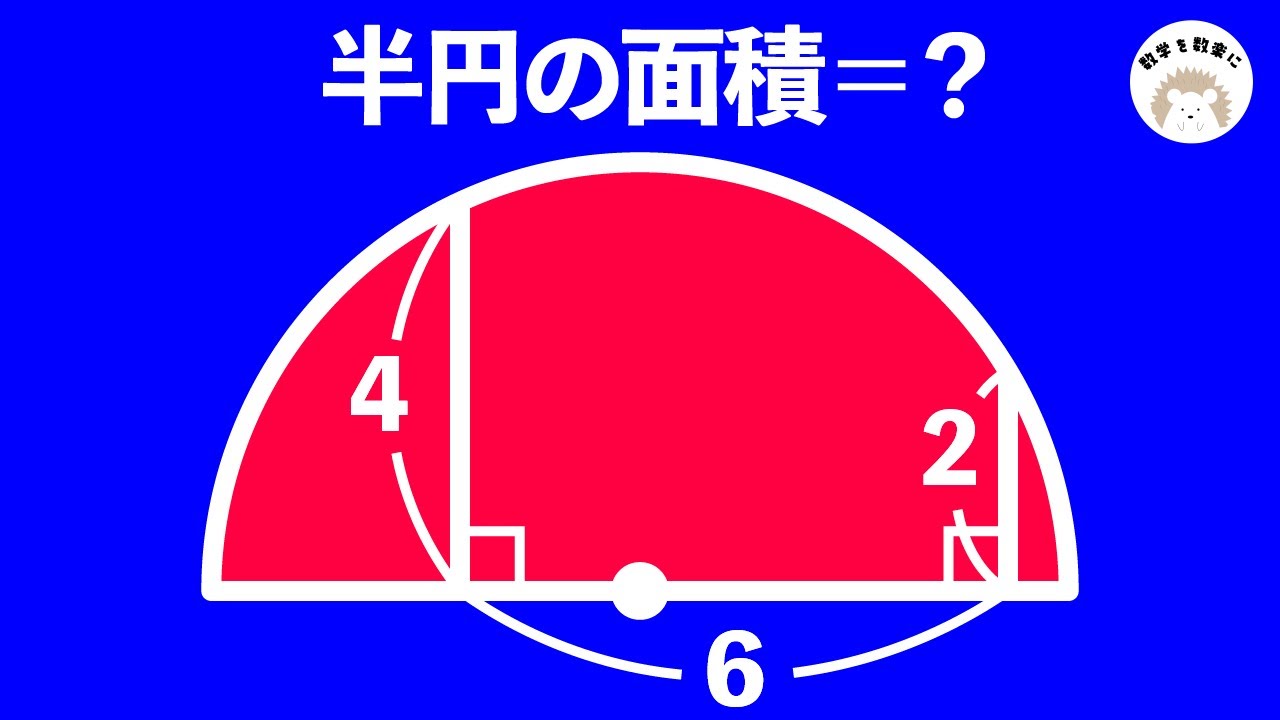
半円の面積🟰❓ (area of semicircle🟰❓)
【数学】中高一貫校問題集2幾何158:三平方の定理:線分の長さ

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
この動画を見る
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何157:三平方の定理:三角形の面積

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
この動画を見る
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
【数学】中高一貫校問題集2幾何156:直角三角形の3辺の長さの決定

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
この動画を見る
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
2通りで解説 円の面積

おうぎ形と正方形
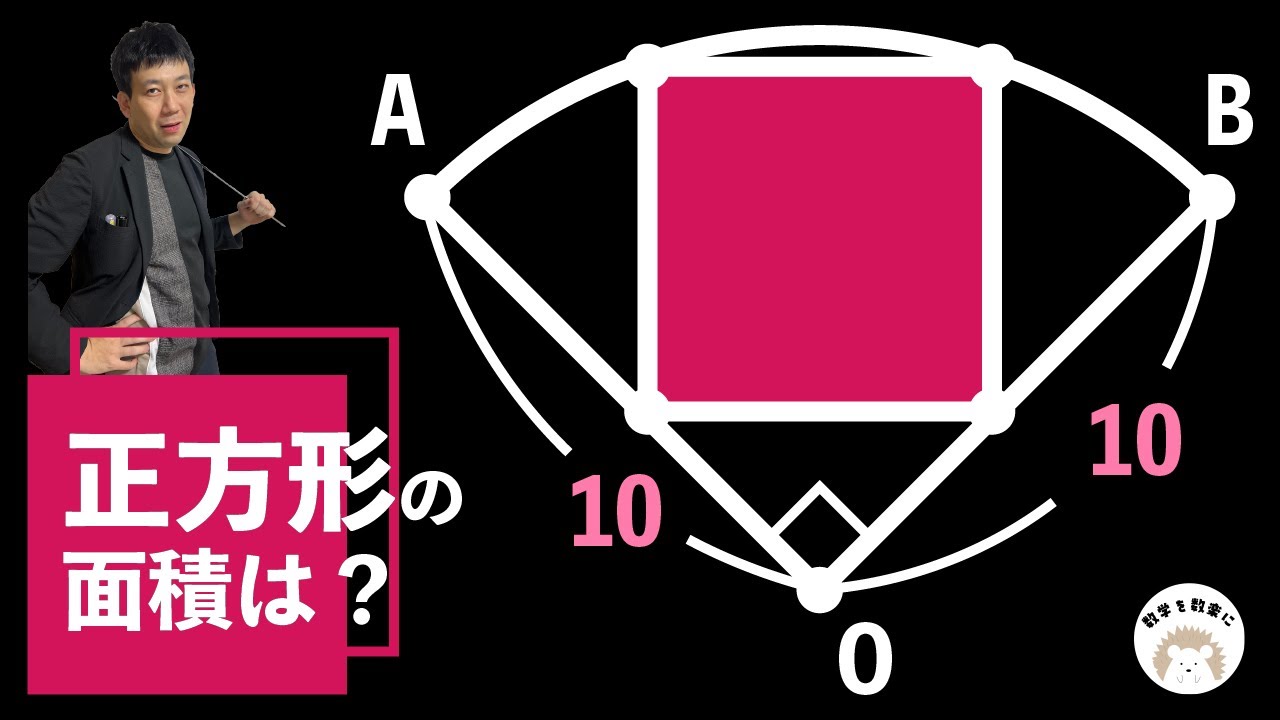
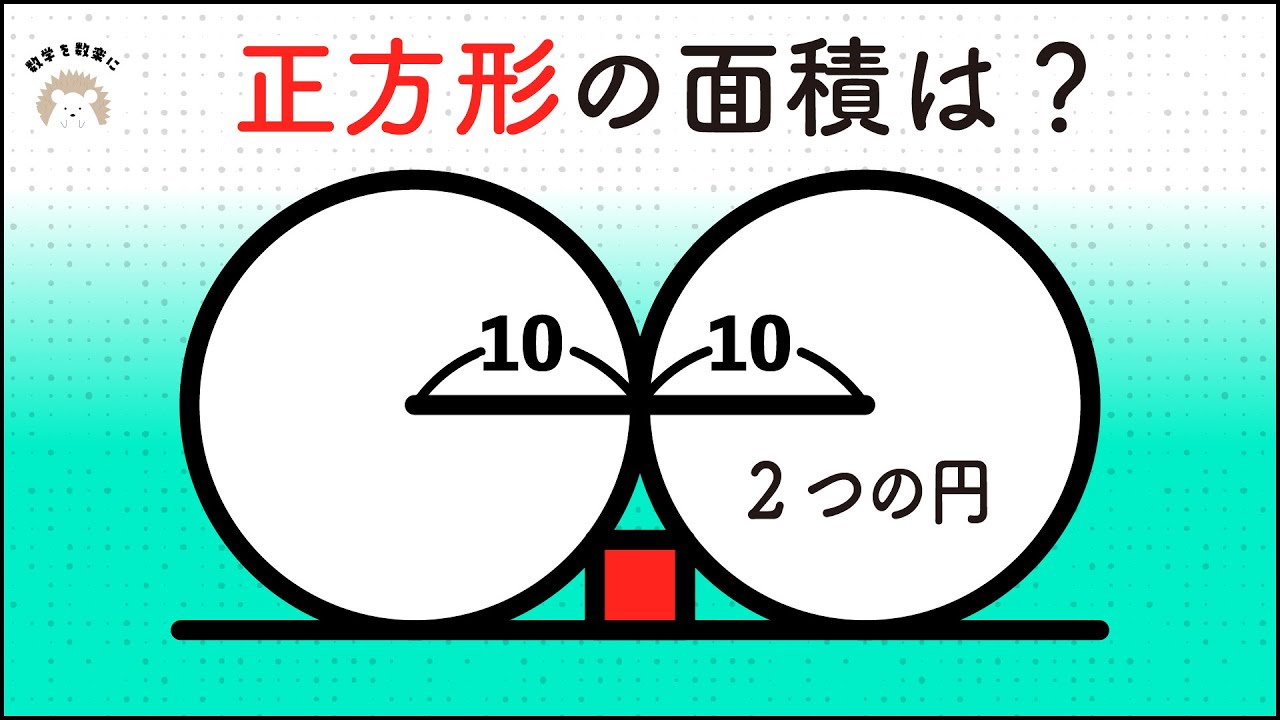
2つの円と正方形
補助線引けるかな?円の面積=?

この問題一瞬で解ける?

正八角形と円

さすがに知ってる?

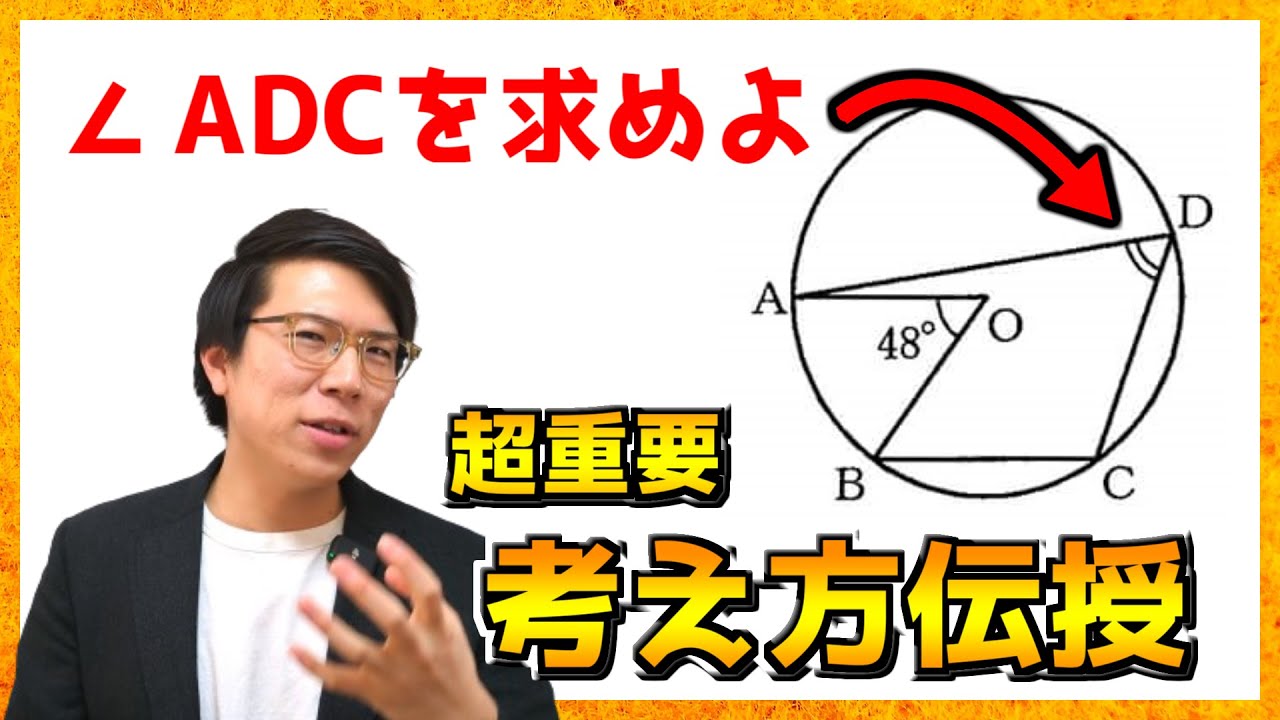
【中学数学】円周角の問題演習~2023年愛知県公立高校入試~【高校受験】
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2023年度の愛知県公立高校入試大問3の過去問解説です
この動画を見る
2023年度の愛知県公立高校入試大問3の過去問解説です
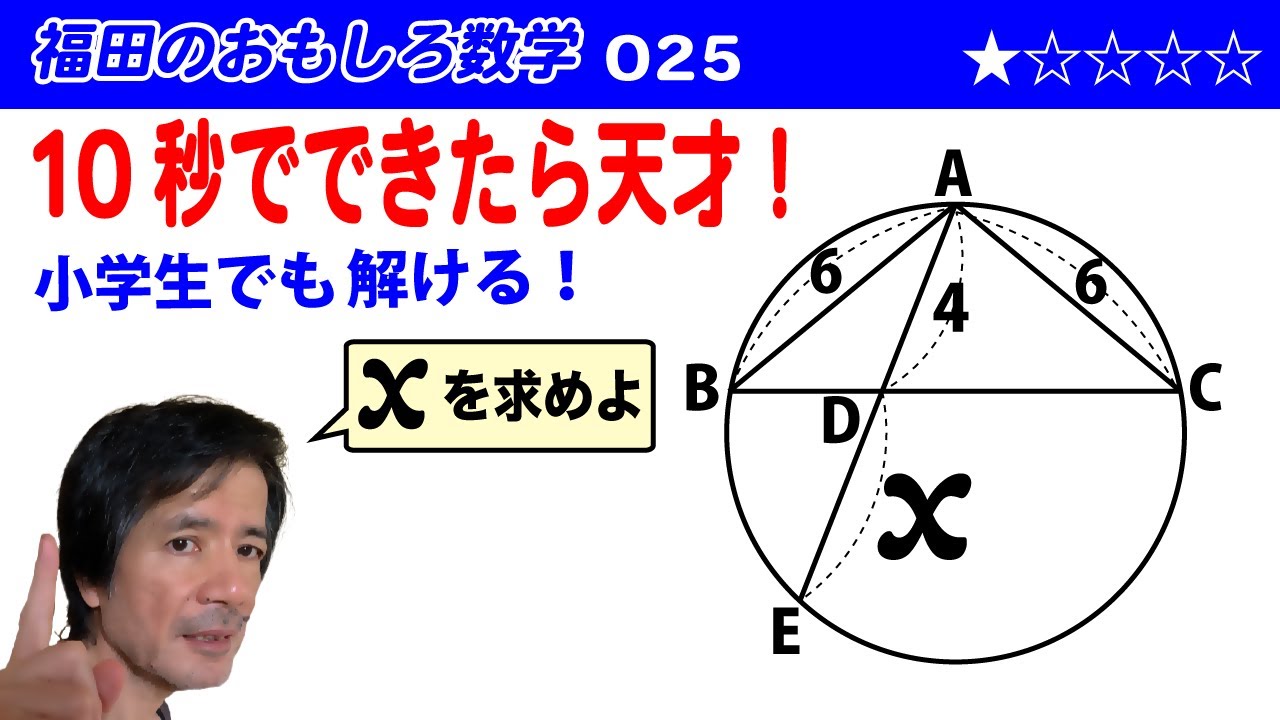
福田のおもしろ数学025〜10秒でできたら天才〜円に内接する二等辺三角形と線分の長さ
単元:
#数学(中学生)#中3数学#数A#図形の性質#円#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
小学生でも解ける!?
xを求めよ
図は動画内参照
この動画を見る
小学生でも解ける!?
xを求めよ
図は動画内参照
3.14を逆さにしたらPIE?

【フル】円周率にπが使われる理由とは?

【円周率が「分かる」…!】無理数:青山学院高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
円に内接/外接する$ \color{red}{正方形・正六角形}$について考察すると
$ \Box \color{red}{\lt \pi \lt}\Box $が成り立つことが分かる.
$ \Box $を解け.
青山学院高等部過去問
この動画を見る
円に内接/外接する$ \color{red}{正方形・正六角形}$について考察すると
$ \Box \color{red}{\lt \pi \lt}\Box $が成り立つことが分かる.
$ \Box $を解け.
青山学院高等部過去問
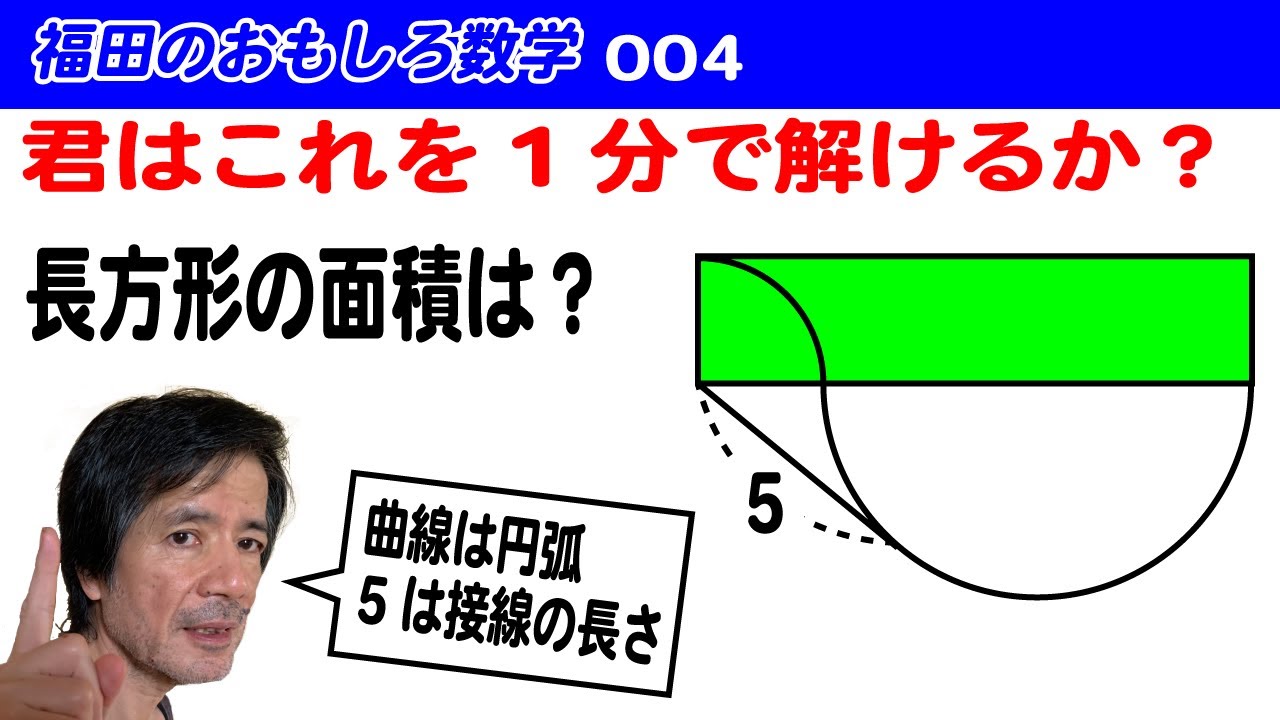
福田のおもしろ数学004〜接線の長さしかわからない〜長方形の面積を求める
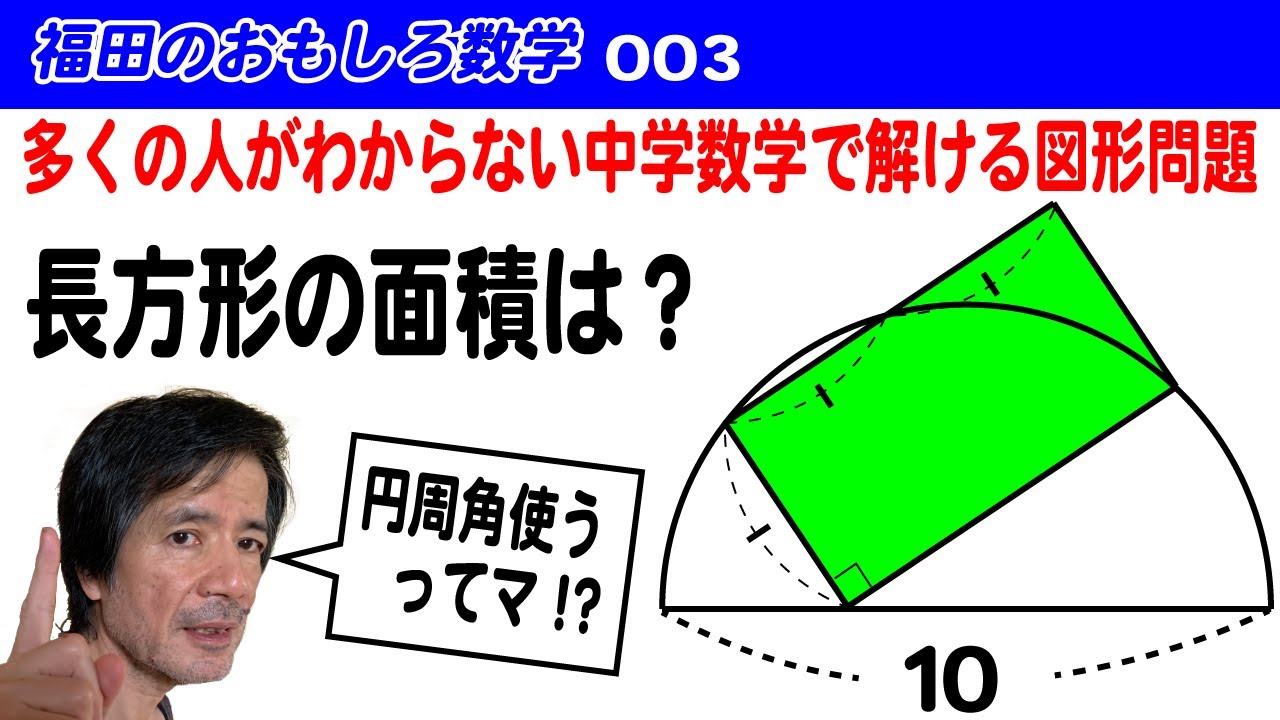
福田のおもしろ数学〜円周角の定理を使うってマ?〜長方形の面積を求める
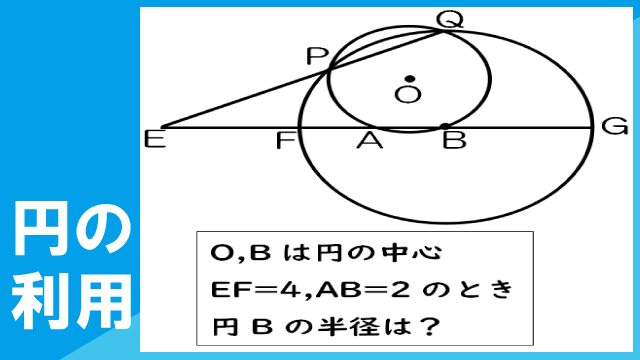
【数学】中高一貫校問題集2幾何150:円:2つの円 方べきの定理の利用
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、2つの円O、Bが2点P、Qで交わり、さらに、円Oは円Bの直径FGと2点A、Bで交わっている。点Bは円Bの中心である。また、点Eは2直線PQ、FGの交点である。EF=4、AB=2のとき、円Bの半径を求めなさい。
この動画を見る
図のように、2つの円O、Bが2点P、Qで交わり、さらに、円Oは円Bの直径FGと2点A、Bで交わっている。点Bは円Bの中心である。また、点Eは2直線PQ、FGの交点である。EF=4、AB=2のとき、円Bの半径を求めなさい。
