 数学オリンピック
数学オリンピック
 数学オリンピック
数学オリンピック
こんなの解けるわけなくない!?算数オリンピックの難問!【中学受験算数】
単元:
#算数(中学受験)#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形その他#数学オリンピック
指導講師:
こばちゃん塾
問題文全文(内容文):
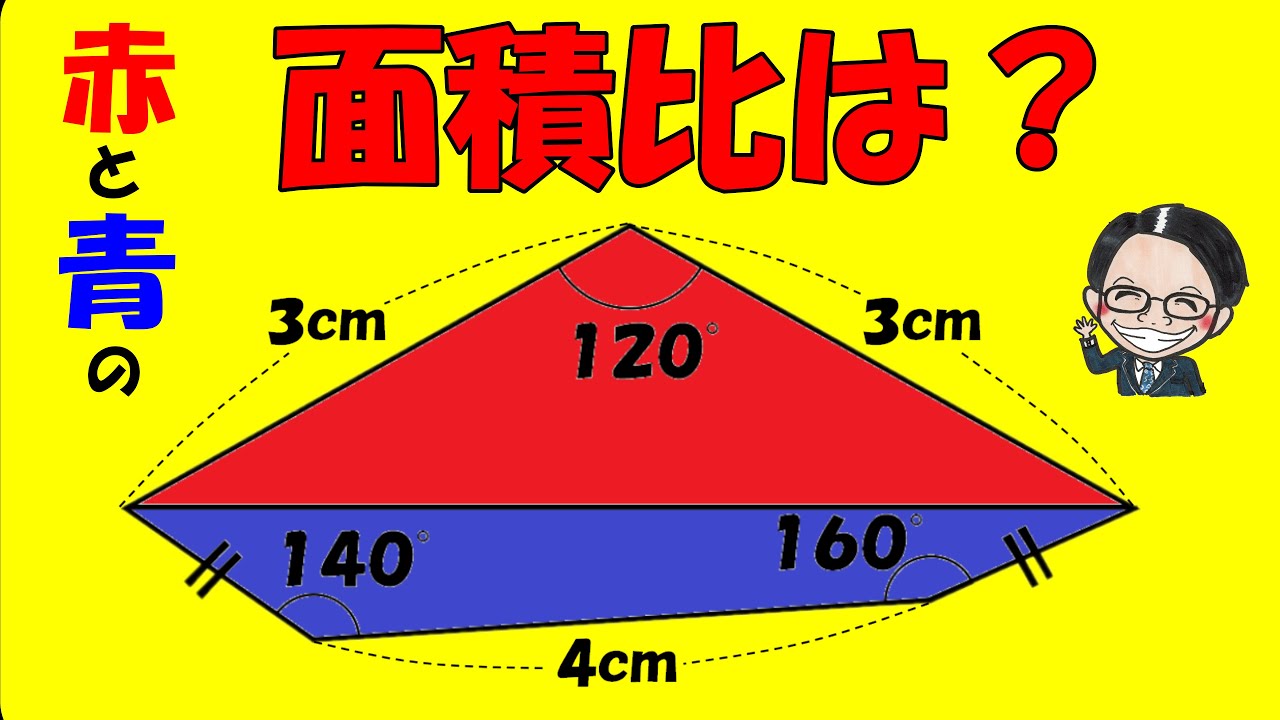
三角形ABEと四角形BCDEの面積比は?
*図は動画内参照
この動画を見る
三角形ABEと四角形BCDEの面積比は?
*図は動画内参照
福田のおもしろ数学210〜2つ対称式の条件から和を求める

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
この動画を見る
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
ルートと階乗

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#場合の数#数学オリンピック#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{ \displaystyle \frac{123!-122!}{122!-121!} }$
出典:数学オリンピック
この動画を見る
$\sqrt{ \displaystyle \frac{123!-122!}{122!-121!} }$
出典:数学オリンピック
福田のおもしろ数学140〜不等式の証明とRavi変換

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#恒等式・等式・不等式の証明#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$, $b$, $c$が三角形の3辺の長さのとき次の不等式を証明せよ。
$a^2(b+c-a)$+$b^2(c+a-b)$+$c^2(a+b-c)$≦$3abc$
この動画を見る
$a$, $b$, $c$が三角形の3辺の長さのとき次の不等式を証明せよ。
$a^2(b+c-a)$+$b^2(c+a-b)$+$c^2(a+b-c)$≦$3abc$
福田のおもしろ数学053〜数学オリンピックの幾何の問題〜線分の長さを求める
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#方べきの定理と2つの円の関係#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
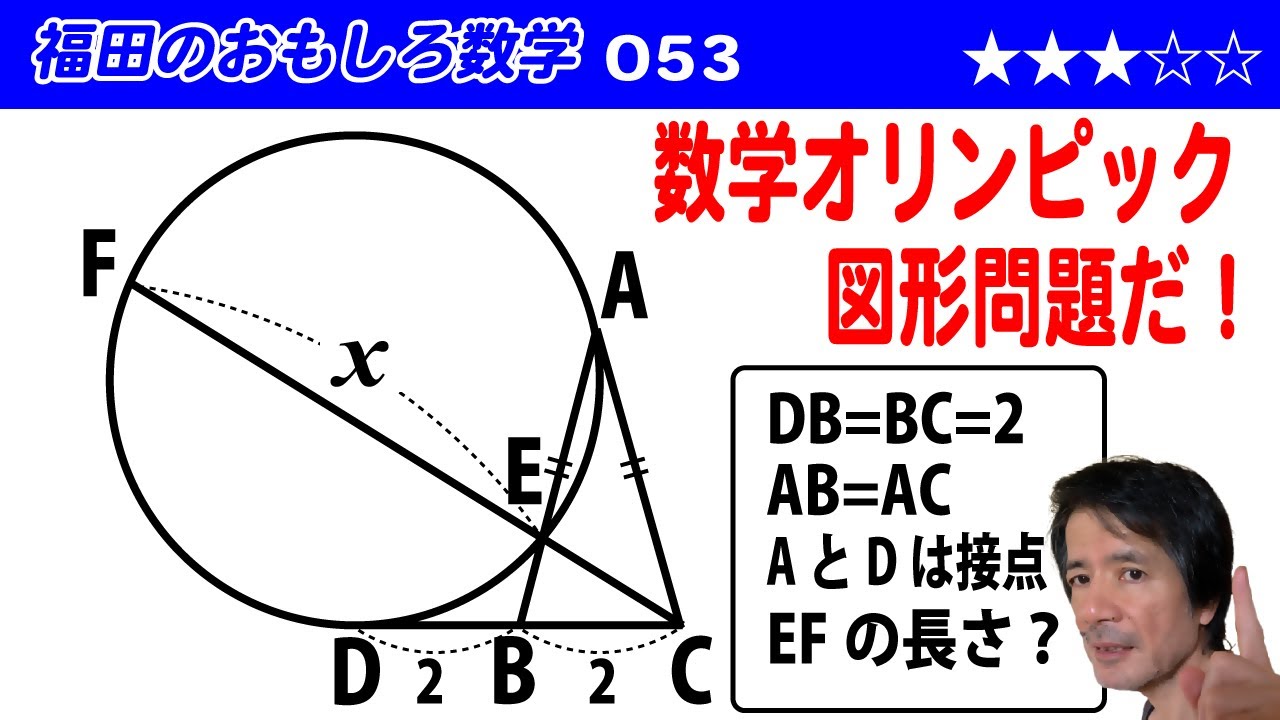
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
数学オリンピック過去問
この動画を見る
DB = BC = 2 , AB = AC, 直線 AC と直線 DC は点 A, D で円 O に接している。
直線AB と円 O の交点のうち A でない方を E とし、直線 CE と円 O の交点のうち E でない方を F とする。
線分 EF の長さを求めよ。
※図は動画内参照
数学オリンピック過去問
福田のおもしろ数学050〜数学オリンピックの問題〜2変数関数の最小

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
実数a,bが$a+b=17$を満たすとき$2^a+4^b$の最小値を求めよ
数学オリンピック過去問
この動画を見る
実数a,bが$a+b=17$を満たすとき$2^a+4^b$の最小値を求めよ
数学オリンピック過去問
福田のおもしろ数学035〜2001年数学オリンピックの名作〜13で割った余りを求める

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
$1^{2001}+2^{2001}+3^{2001}+…+2001^{2001}$を13で割ったあまりを求めよ
2001数学オリンピック過去問
この動画を見る
$1^{2001}+2^{2001}+3^{2001}+…+2001^{2001}$を13で割ったあまりを求めよ
2001数学オリンピック過去問
福田のおもしろ数学019〜ジュニア数学オリンピック本選問題〜直角三角形の斜辺の長さを求める

単元:
#数学(中学生)#中3数学#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直角三角形の一辺の長さが 18 で、すべての辺の長さが整数のとき、斜辺の長さは?
ジュニア数学オリンピック過去問
この動画を見る
直角三角形の一辺の長さが 18 で、すべての辺の長さが整数のとき、斜辺の長さは?
ジュニア数学オリンピック過去問
福田のおもしろ数学016〜ジュニア数学オリンピック予選問題〜正三角形の面積
単元:
#算数(中学受験)#数学(中学生)#中1数学#中2数学#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形#三角形と四角形#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
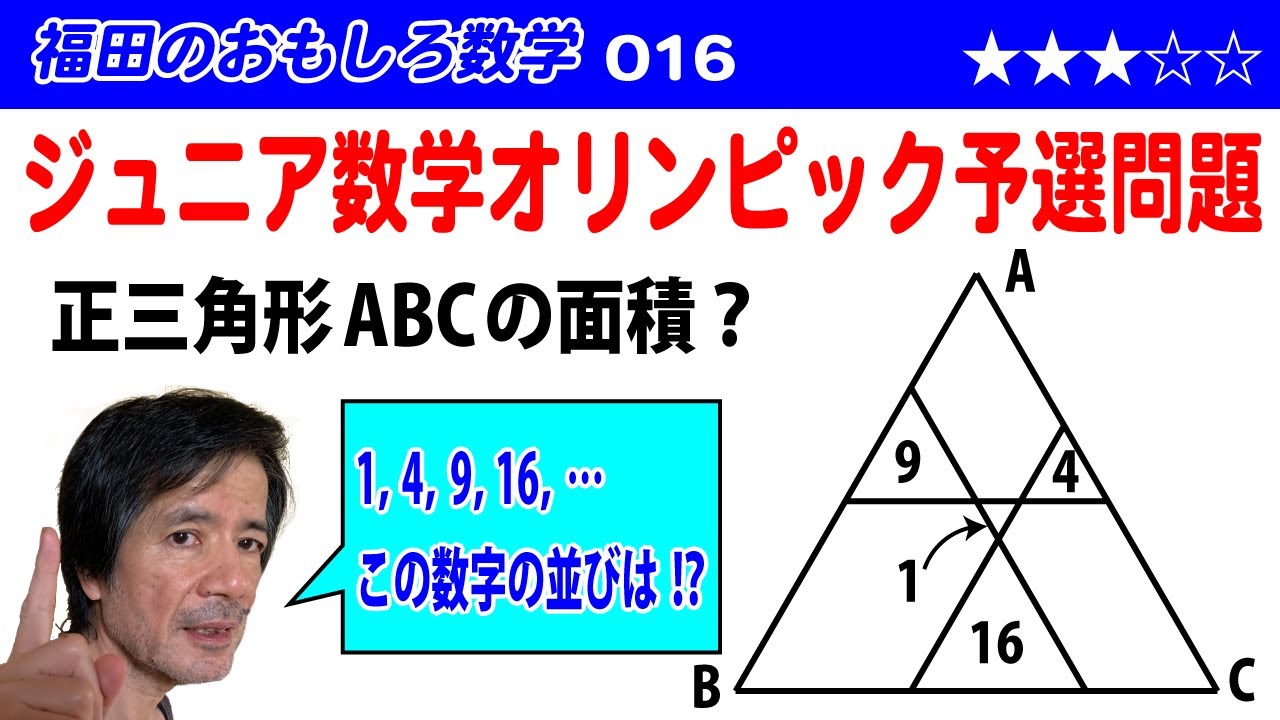
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
この動画を見る
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
福田のおもしろ数学015〜ジュニア数学オリンピック本戦問題〜2つの式を満たす4つの自然数を求める

単元:
#数学(中学生)#中2数学#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
福田のおもしろ数学013〜ジュニア数学オリンピックから〜条件を満たす6個の変数は

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ.
ジュニア数学オリンピック過去問
この動画を見る
$a,b,c,d,e,f$は相異なる1以上9以下の整数
$ab=cd=e+f$のとき、
$a+b+c+d+e+f$
として考えられる値をすべて求めよ.
ジュニア数学オリンピック過去問
バングラデシュ数学オリンピック
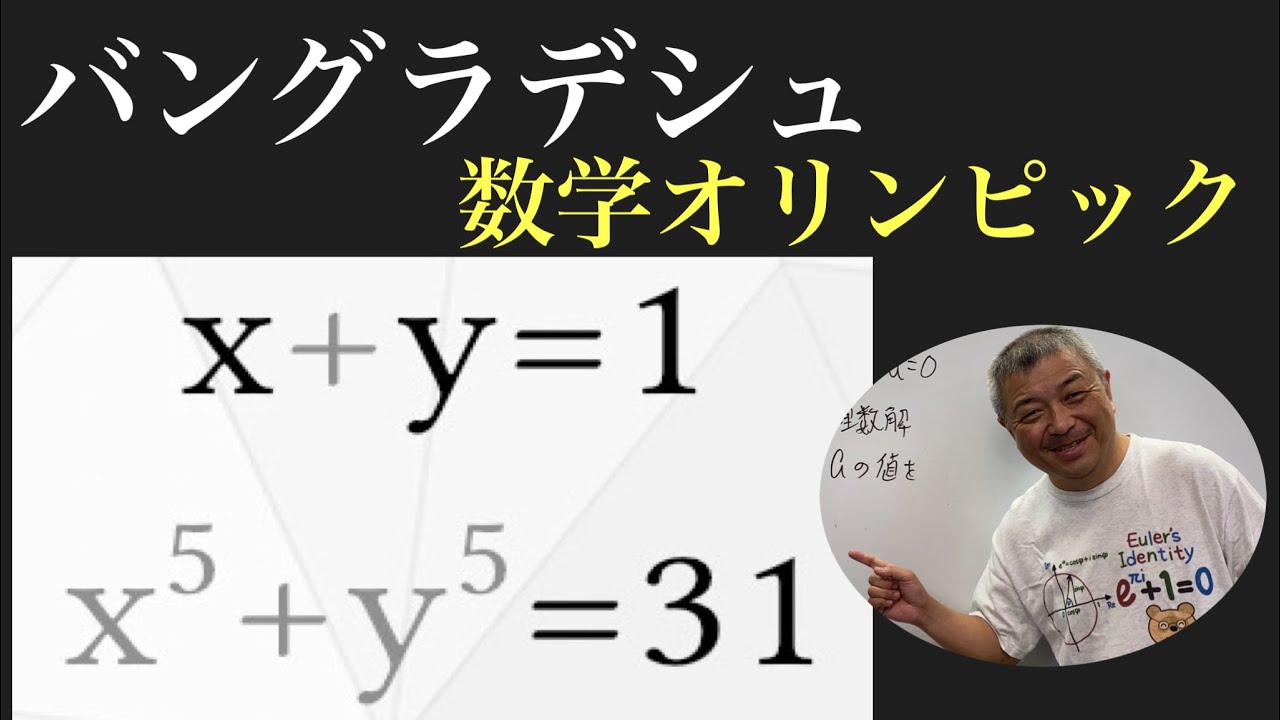
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$
\begin{cases}
x+y = 1 \\
x^5+y^5 = 31
\end{cases}
$
バングラデシュ数学オリンピック過去問
この動画を見る
$
\begin{cases}
x+y = 1 \\
x^5+y^5 = 31
\end{cases}
$
バングラデシュ数学オリンピック過去問
オーストラリア数学オリンピックAustralian math Olypmpiad

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{13}+2^{10}+2^x=y^2$
自然数x,yを求めよ.
オーストラリア数学オリンピック過去問
この動画を見る
$2^{13}+2^{10}+2^x=y^2$
自然数x,yを求めよ.
オーストラリア数学オリンピック過去問
日本Jr 数学オリンピック 平方数

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$21,221,2221,22221,…$の中には平方数がないことを示せ.
日本jr数学オリンピック過去問
この動画を見る
$21,221,2221,22221,…$の中には平方数がないことを示せ.
日本jr数学オリンピック過去問
数学オリンピック日本予選 合同式の基本
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
この動画を見る
$1111^{2018}$を$11111$で割ったあまりを求めよ.
数学オリンピック過去問
モスクワ数学オリンピック 整数

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは自然数とするとき,
$1!+2!+3!+・・・・・・+x!=y^2$を求めよ.
モスクワ数学オリンピック過去問
この動画を見る
x,yは自然数とするとき,
$1!+2!+3!+・・・・・・+x!=y^2$を求めよ.
モスクワ数学オリンピック過去問
数学オリンピック予選

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
この動画を見る
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
アジア太平洋数学オリンピックのナイスな整数問題

単元:
#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,b,cは自然数である.
$a^2+b+c,a+b^2+c,a+b+c^2$
この3つのすべてが平方数になることはないことを示せ.
アジア太平洋数学オリンピック過去問
この動画を見る
a,b,cは自然数である.
$a^2+b+c,a+b^2+c,a+b+c^2$
この3つのすべてが平方数になることはないことを示せ.
アジア太平洋数学オリンピック過去問
【数学オリンピックに挑戦】下3桁じゃなく上3桁!?【数学】

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
6桁の平方数の上3桁として考えられるものは全部でいくつあるか。
数学オリンピック過去問
この動画を見る
6桁の平方数の上3桁として考えられるものは全部でいくつあるか。
数学オリンピック過去問
問題の背景を探る ハンガリーJr数学Olympic
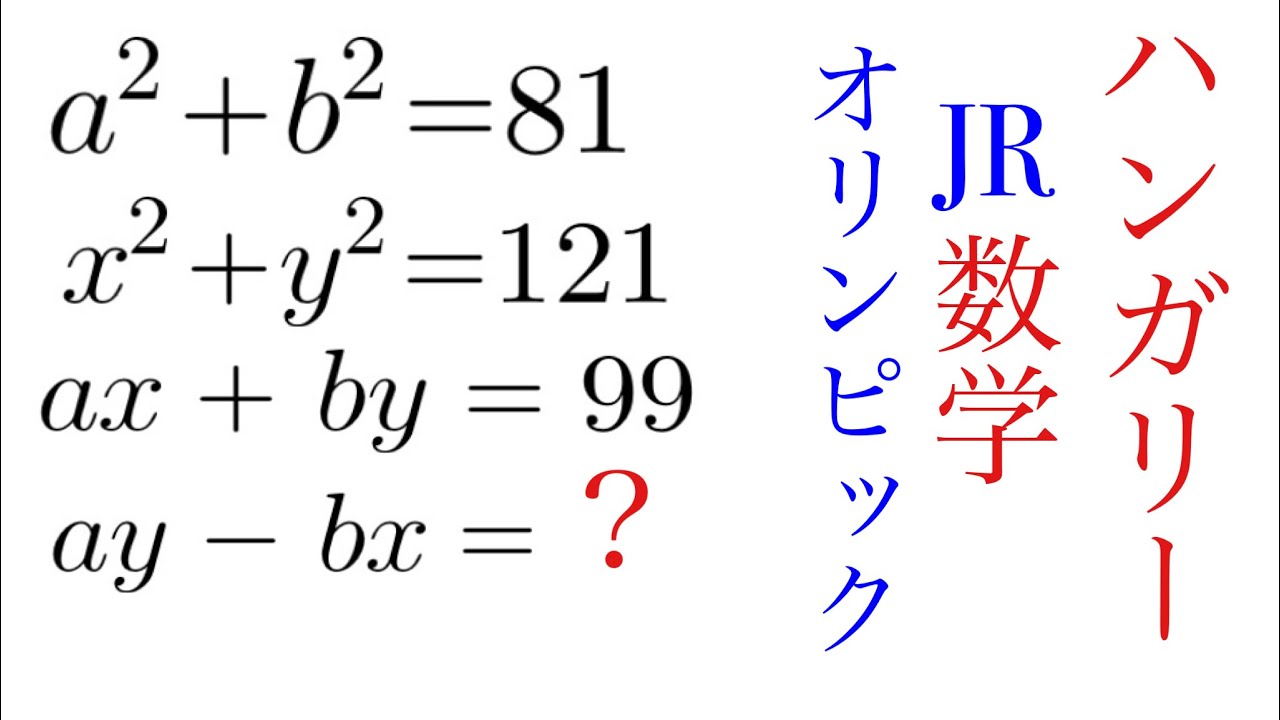
単元:
#複素数平面#円#三角関数#複素数#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
この動画を見る
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
【数学】数学オリンピックの組み合わせ論の問題、見方を教えます!

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
理数個別チャンネル
問題文全文(内容文):
1998×2002マスのマス目があり、黒と白の市松模様に塗られている。マス目に0か1を書き加えたところ、各行・各列に1が書かれた個数は奇数個であった。このとき白マスの1は偶数個あることを示せ。
この動画を見る
1998×2002マスのマス目があり、黒と白の市松模様に塗られている。マス目に0か1を書き加えたところ、各行・各列に1が書かれた個数は奇数個であった。このとき白マスの1は偶数個あることを示せ。
シンガポール数学オリンピックの問題
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学オリンピック#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
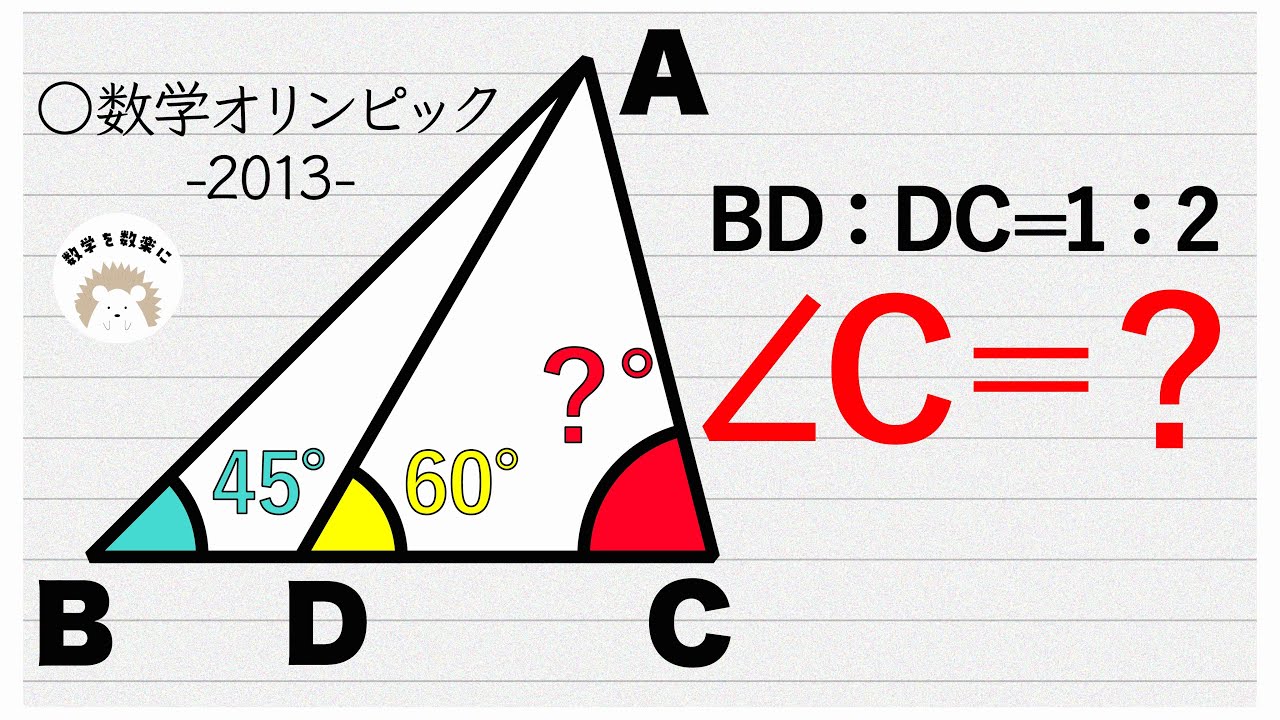
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
この動画を見る
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
数学ゴールデン#2【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。
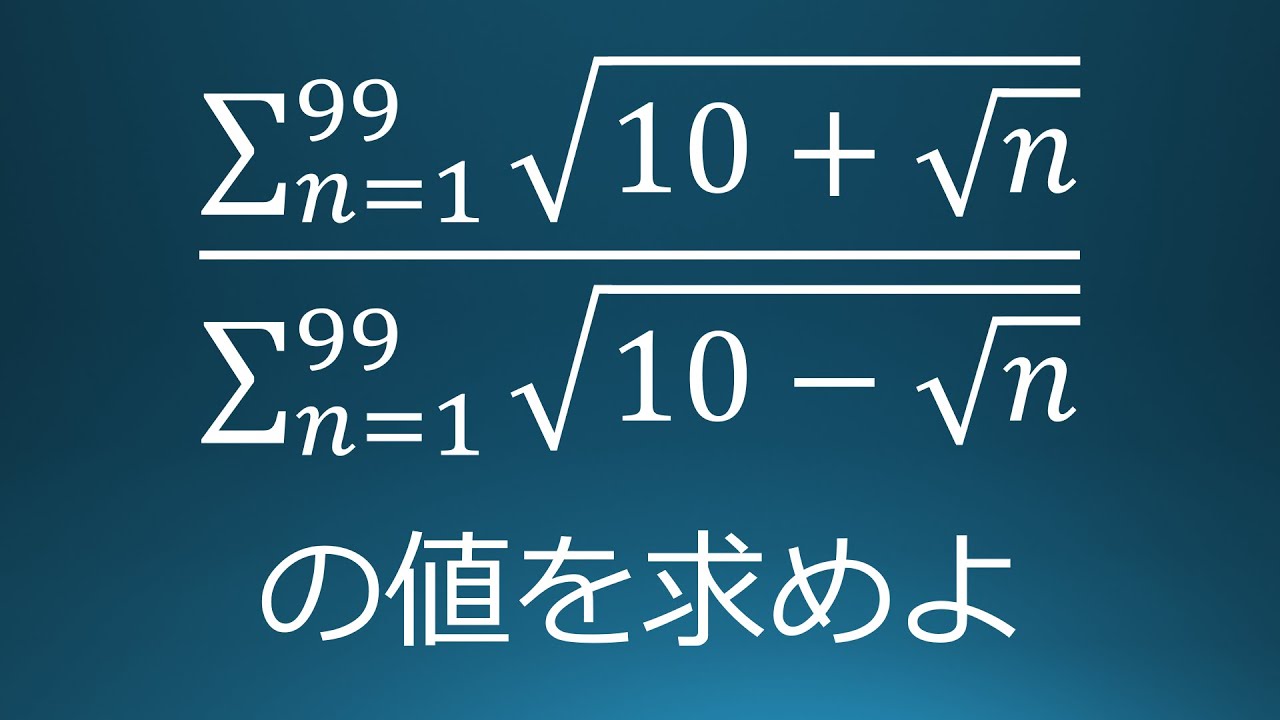
単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{\sqrt{ 10+\sqrt{ 1 } }+\sqrt{ 10+\sqrt{ 2 } }+・・・+\sqrt{ 10+\sqrt{ 99 } }}{\sqrt{ 10-\sqrt{ 1 } }+\sqrt{ 10-\sqrt{ 2 } }+・・・+\sqrt{ 10-\sqrt{ 99 } }}$を計算せよ。
出典:数学ゴールデン 数学オリンピック
この動画を見る
$\displaystyle \frac{\sqrt{ 10+\sqrt{ 1 } }+\sqrt{ 10+\sqrt{ 2 } }+・・・+\sqrt{ 10+\sqrt{ 99 } }}{\sqrt{ 10-\sqrt{ 1 } }+\sqrt{ 10-\sqrt{ 2 } }+・・・+\sqrt{ 10-\sqrt{ 99 } }}$を計算せよ。
出典:数学ゴールデン 数学オリンピック
数学ゴールデン【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \lt x$:実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典:数学ゴールデン 数学オリンピック
この動画を見る
$0 \lt x$:実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典:数学ゴールデン 数学オリンピック
練習問題35 数学オリンピックの問題 複素数を利用して証明してみた。

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学オリンピック#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2}{7}\pi+\cos\dfrac{3}{7}\pi=\dfrac{1}{2}$
を示せ.
2通りの解説 ジュニア数学オリンピック B
ギリシア 数学オリンピック 簡単

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3・2^x+4-n^2$
$x,n$は自然数とする.$x$の値を求めよ.
この動画を見る
$3・2^x+4-n^2$
$x,n$は自然数とする.$x$の値を求めよ.
数学オリンピック トルコ 標準レベル

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は整数であり,$P$は素数である.
$x^2-3xy+P^2y^2=12P$
$(x,y,P)$の組をすべて求めよ.
数学オリンピックトルコ過去問
この動画を見る
$x,y$は整数であり,$P$は素数である.
$x^2-3xy+P^2y^2=12P$
$(x,y,P)$の組をすべて求めよ.
数学オリンピックトルコ過去問
数学オリンピック ベラルーシ 整数

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
この動画を見る
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
アルゼンチンの数学オリンピック

単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$は素数であり,$p^5+p^3+2=q^2-q$
$(p,q)$をすべて求めよ.
この動画を見る
$p,q$は素数であり,$p^5+p^3+2=q^2-q$
$(p,q)$をすべて求めよ.
