 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学360〜1が連続1991個並ぶ数は素数か

福田のおもしろ数学359〜nのn-7分の1乗が整数となる8以上のnを求める

福田のおもしろ数学358〜定積分の計算

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$I=\int_0^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx$の値を求めて下さい。
この動画を見る
$I=\int_0^{\frac{\pi}{2}} \frac{\sin^3 x}{\sin x + \cos x} dx$の値を求めて下さい。
福田のおもしろ数学358〜定積分の計算

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$I=\int_0^\frac{\pi}{2} \frac{\sin^3 x}{\sin x+\cos x} dx$の値を求めて下さい。
この動画を見る
$I=\int_0^\frac{\pi}{2} \frac{\sin^3 x}{\sin x+\cos x} dx$の値を求めて下さい。
福田のおもしろ数学357〜シグマで表された式の定積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\int_0^\pi (\sum_{k=1}^n \sin kx)^2 dx$ を計算して下さい。
この動画を見る
$\displaystyle\int_0^\pi (\sum_{k=1}^n \sin kx)^2 dx$ を計算して下さい。
福田のおもしろ数学356〜2つのルートの和が自然数となる条件

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{n}$と$\sqrt{n+2025}$が自然数となるような自然数$n$をすべて求めて下さい。
この動画を見る
$\sqrt{n}$と$\sqrt{n+2025}$が自然数となるような自然数$n$をすべて求めて下さい。
福田のおもしろ数学355〜3次の不定方程式の解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y$ は $0$ 以上の整数で、$y^3=x^3+8x^2-6x+8$ を満たしている。このような $(x,y)$ の組をすべて求めて下さい。
この動画を見る
$x,y$ は $0$ 以上の整数で、$y^3=x^3+8x^2-6x+8$ を満たしている。このような $(x,y)$ の組をすべて求めて下さい。
福田のおもしろ数学354〜指数方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
この動画を見る
$2^x+3^x-4^x+6^x-9^x=1$ を満たす実数 $x$ をすべて求めて下さい。
福田のおもしろ数学353〜1が連続3^n個並ぶ数は3^nで割り切れることの証明
単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
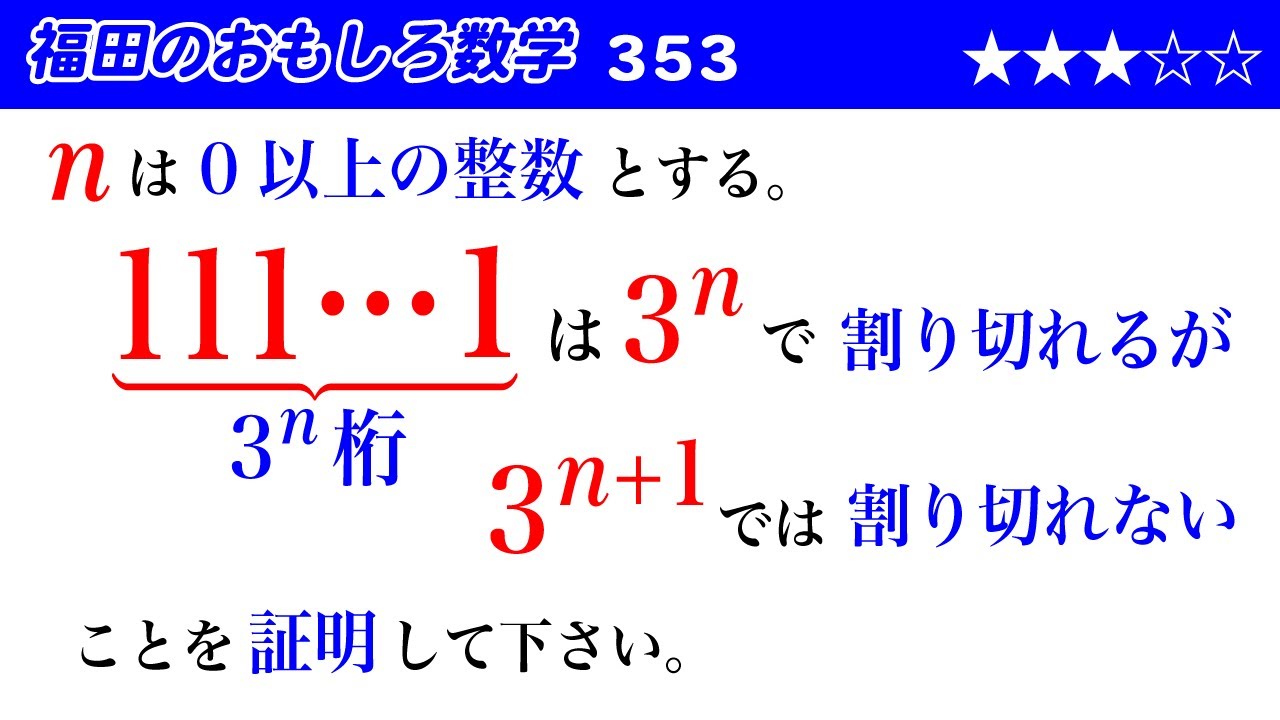
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
この動画を見る
$n$ は $0$ 以上の整数とする。$\underbrace{ 111\cdots111 }_{3^n 桁}$ は $3^n$ で割り切れるが、 $3^{n+1}$ で割り切れないことを証明してください。
福田のおもしろ数学352〜三角形の3辺の長さと周の長さと面積

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$3$ 辺の長さが $a,a,b$、周の長さが $P$、面積が $A$ の三角形がある。$b$ と $P$ が整数かつ $P=A^2$ のとき、$(a,b)$ を求めよ。
この動画を見る
$3$ 辺の長さが $a,a,b$、周の長さが $P$、面積が $A$ の三角形がある。$b$ と $P$ が整数かつ $P=A^2$ のとき、$(a,b)$ を求めよ。
福田のおもしろ数学351〜漸化式で定まる数列の第2025項の取り得る値の個数

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
この動画を見る
$a_1 = 1, a_{n+1} + a_n = ( a_{n+1} - a_n )^2$ で定まる、すべての項が正の数列 $\{ a_n \}$ に対し $a_2025$ の取りうる値は何個あるか。
福田のおもしろ数学350〜100日間開催される催しに75日参加する6人の生徒が少なくとも5人以上参加する日数

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$100$ 日間開催される催しに $75$ 日参加する生徒が $6$ 人いる。各生徒は参加する日を $100$ 日の中から自由に選べる。少なくとも $5$ 人が参加した日が $n$ 日あった。
$n$ の最大値と最小値を求めよ。
この動画を見る
$100$ 日間開催される催しに $75$ 日参加する生徒が $6$ 人いる。各生徒は参加する日を $100$ 日の中から自由に選べる。少なくとも $5$ 人が参加した日が $n$ 日あった。
$n$ の最大値と最小値を求めよ。
福田のおもしろ数学348〜不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
この動画を見る
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
福田のおもしろ数学347〜余りを求める問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
整数$a$に対して$a^2$を自然数$n$で割ると1余る。次の各場合に$a$を$n$で割った余りを求めて下さい。$(1)n=16 (2)n=3^k$ ($k$は自然数)
この動画を見る
整数$a$に対して$a^2$を自然数$n$で割ると1余る。次の各場合に$a$を$n$で割った余りを求めて下さい。$(1)n=16 (2)n=3^k$ ($k$は自然数)
福田のおもしろ数学345〜複雑な2重根号の式が整数となる条件

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
この動画を見る
$\sqrt{ \mathstrut \frac{25}{2} +\sqrt{ \mathstrut \frac{625}{4} -n}}$+$\sqrt{ \mathstrut \frac{25}{2} -\sqrt{ \mathstrut \frac{625}{4} -n}}$が整数となるような整数$n$をすべて求めよ。
福田のおもしろ数学344〜条件付き最小値問題と絶対値の処理

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
この動画を見る
$\log_{ 4 }( x+2y)+\log_{ 4 } (x-2y)=1$のとき、$|x|ー|y|$の最小値を求めよ。
福田のおもしろ数学343〜3次方程式の解の存在範囲

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
この動画を見る
$1 \geq a \geq b \geq c >0$ のとき $x^3+a x^2+bx+c=0$ の1つの解を $\alpha$ とする。
$|a| \leq 1$ を証明してください。
福田のおもしろ数学342〜複素数に関する三角不等式と等号成立条件

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
この動画を見る
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
福田のおもしろ数学341〜関数方程式を解く

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
この動画を見る
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
福田のおもしろ数学340〜三角関数の最大値

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$-\dfrac{5}{12}\pi \leqq x \leqq -\dfrac{\pi}{3}$のとき
$y=\tan(x+\dfrac23\pi)-\tan(x+\dfrac\pi6)+\cos(x+\dfrac\pi6)$
の最大値を求めて下さい。
この動画を見る
$-\dfrac{5}{12}\pi \leqq x \leqq -\dfrac{\pi}{3}$のとき
$y=\tan(x+\dfrac23\pi)-\tan(x+\dfrac\pi6)+\cos(x+\dfrac\pi6)$
の最大値を求めて下さい。
福田のおもしろ数学339〜自然数の列から平方数を除いてできる列の第2024項の値

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
この動画を見る
自然数の列$1,2,3,\cdots$から平方数を除いてできる列を$a_1,a_2,a_3,\cdots$とする。$a_{2024}$を求めて下さい。
福田のおもしろ数学338〜不定方程式の整数解

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a^2+b=b^{2025}$を満たす整数$a,b$を求めて下さい。
この動画を見る
$a^2+b=b^{2025}$を満たす整数$a,b$を求めて下さい。
福田のおもしろ数学337〜定積分の計算

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-1}^1\log(x+\sqrt{x^2+1})dx$
を計算して下さい。
この動画を見る
$\displaystyle \int_{-1}^1\log(x+\sqrt{x^2+1})dx$
を計算して下さい。
福田のおもしろ数学336〜連続する奇数の素数の和は3つ以上の因数をもつ証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
連続する奇数の素数$p,q$に対し$p+q$は$1$より大きい3個以上の整数の積で表される。これを証明してください。
この動画を見る
連続する奇数の素数$p,q$に対し$p+q$は$1$より大きい3個以上の整数の積で表される。これを証明してください。
福田のおもしろ数学335〜三角形に関する三角不等式の証明

福田のおもしろ数学334〜sin3°の値を求める

福田のおもしろ数学333〜整数部分と小数部分の積に関する方程式の解

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$次の方程式を満たすxを求めよ。[ x ]はxの整数部分、( x )はxの小数部分を表す。$$
$$[ x ]\cdot( x )=2024x$$
この動画を見る
$$次の方程式を満たすxを求めよ。[ x ]はxの整数部分、( x )はxの小数部分を表す。$$
$$[ x ]\cdot( x )=2024x$$
福田のおもしろ数学332〜不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
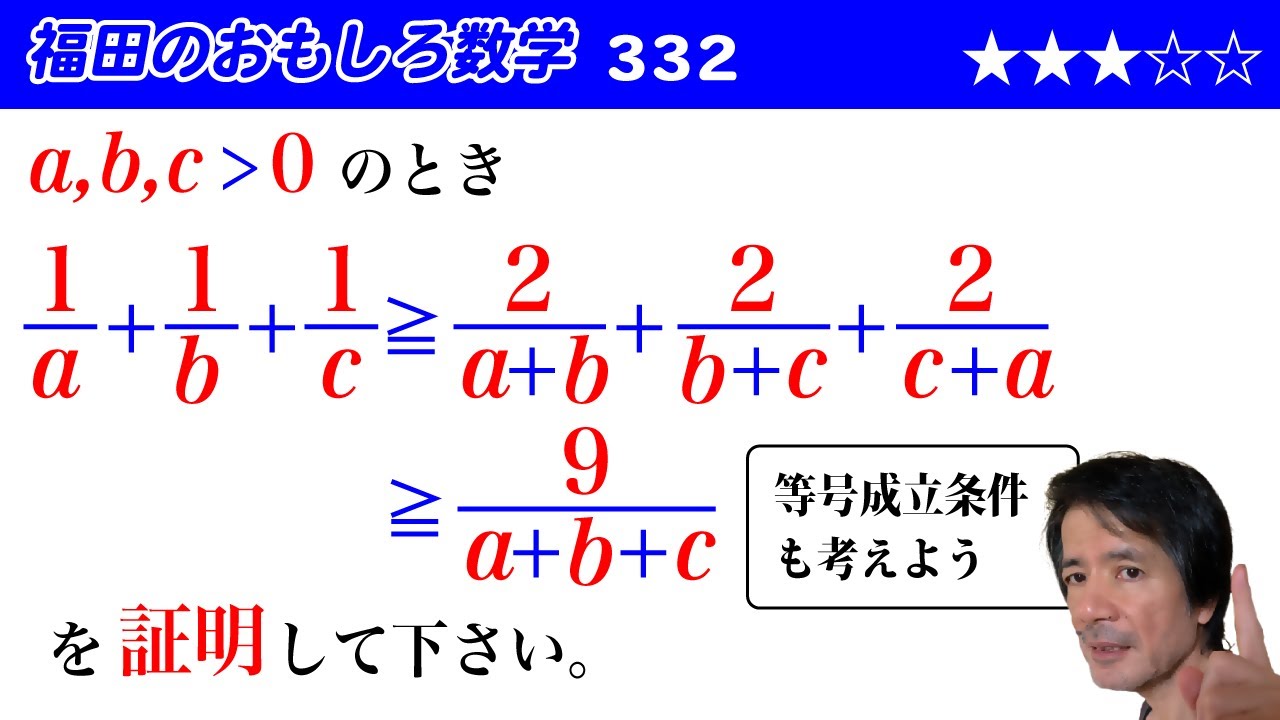
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
この動画を見る
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
福田のおもしろ数学331〜連立の不定方程式の整数解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
この動画を見る
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
福田のおもしろ数学330〜三角形の成立条件と条件を満たす三角形の個数

単元:
#数A#図形の性質#整数の性質#三角形の辺の比(内分・外分・二等分線)#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数$n\geqq 3$に対して$f(n)$を各辺の長さが整数かつ周の長さが$n$である三角形の個数で定義する。
(例えば$f(3)=1,f(4)=0,f(7)=2$である)
$f(1999)\geq f(1966),f(2000)=f(1997)$を示せ。
この動画を見る
自然数$n\geqq 3$に対して$f(n)$を各辺の長さが整数かつ周の長さが$n$である三角形の個数で定義する。
(例えば$f(3)=1,f(4)=0,f(7)=2$である)
$f(1999)\geq f(1966),f(2000)=f(1997)$を示せ。



