 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「100」までの番号の中で、発行されるものは何枚か。
(2)100人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「2888」と書かれたナンバープレートを受け取る人は何人目の人か。
この動画を見る
自動車のナンバープレートの番号を、「1」から「8888」まで順番に発行することにした。ただし4と9という数字をきらう人が多いので、数字4と9を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「100」までの番号の中で、発行されるものは何枚か。
(2)100人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「2888」と書かれたナンバープレートを受け取る人は何人目の人か。
【受験算数】自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「99」までの番号の中で、発行されるものは何枚になるか。
(2)99人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「777」と書かれたナンバープレートを受け取る人は何人目の人か。
この動画を見る
自動車のナンバープレートの番号を、「1」から「999」まで順番に発行することにした。ただし4という数字をきらう人が多いので、数字4を用いた番号は一切使わずに、その番号をとばして順に発行する。
(1)「1」から「99」までの番号の中で、発行されるものは何枚になるか。
(2)99人目の人が受け取るナンバープレートには、どんな番号の数字が書かれているか。
(3)「777」と書かれたナンバープレートを受け取る人は何人目の人か。
【数Ⅲ】【数列の極限】辺AB、ACと円O₁に接する円をO₂とし、辺AB、ACと円O₂に接する円をO₃とする。このように、次々に小さくなる円を作るとき、すべての円の面積の総和を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
正三角形ABCの内接円O₁の半径をrとする。辺AB、ACと円O₁に接する円をO₂とし、辺AB、ACと円O₂に接する円をO₃とする。このように、次々に小さくなる円を作るとき、すべての円の面積の総和を求めよ。
この動画を見る
正三角形ABCの内接円O₁の半径をrとする。辺AB、ACと円O₁に接する円をO₂とし、辺AB、ACと円O₂に接する円をO₃とする。このように、次々に小さくなる円を作るとき、すべての円の面積の総和を求めよ。
【数Ⅲ】【数列の極限】座標平面上で、点Pが原点Oを出発して、x軸の正の向きに1だけ進み、次にy軸の正の向きに1/2だけ進み、次にx軸の負の向きに1/2²だけ進み、次にy軸の負の向きに1/2³だけ進む。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上で、点 $P$ が原点 $O$ を出発して、
$x$ 軸の正の向きに $1$ だけ進み、
次に $y$ 軸の正の向きに $\frac{1}{2}$ だけ進み、
次に $x$ 軸の負の向きに $\frac{1}{2^2}$ だけ進み、
次に $y$ 軸の負の向きに $\frac{1}{2^3}$ だけ進む。
以下、このような運動を限りなく続けるとき、
点 $P$ が近づいていく点の座標を求めよ。
この動画を見る
座標平面上で、点 $P$ が原点 $O$ を出発して、
$x$ 軸の正の向きに $1$ だけ進み、
次に $y$ 軸の正の向きに $\frac{1}{2}$ だけ進み、
次に $x$ 軸の負の向きに $\frac{1}{2^2}$ だけ進み、
次に $y$ 軸の負の向きに $\frac{1}{2^3}$ だけ進む。
以下、このような運動を限りなく続けるとき、
点 $P$ が近づいていく点の座標を求めよ。
【数Ⅲ】【数列の極限】あるボールを床に落とすと、常に落ちる高さの4/5まではね返るという。このボールを2mの高さから落としたとき、床に静止するまでに、このボールが上下する総距離を求めよ。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
あるボールを床に落とすと、常に落ちる高さの4/5まではね返るという。この
ボールを2mの高さから落としたとき、床に静止するまでに、このボールが上下する
総距離を求めよ。
この動画を見る
あるボールを床に落とすと、常に落ちる高さの4/5まではね返るという。この
ボールを2mの高さから落としたとき、床に静止するまでに、このボールが上下する
総距離を求めよ。
【受験算数】どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。
(2)0,3,6,7をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,3,6,7,30,33,…となる。このとき、3776ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べます。1,2,3,5,6,7,8,10,11,…このとき、100番目の数を求めよ。
この動画を見る
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、75番目の数を求めよ。
(2)0,3,6,7をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,3,6,7,30,33,…となる。このとき、3776ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べます。1,2,3,5,6,7,8,10,11,…このとき、100番目の数を求めよ。
【受験算数】どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。
(2)0,2,8をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,2,8,20,22,…となる。このとき、2008ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べる。1,2,3,5,6,7,8,10,11,…このとき、40番目の数を求めよ。
この動画を見る
次の問いに答えなさい。
(1)どの桁も2つの数字1か0を使ってできる1以上の整数を小さいほうから1,10,11,100,101,110,…のように順番に並べたとき、45番目の数を求めよ。
(2)0,2,8をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると、0,2,8,20,22,…となる。このとき、2008ははじめから数えて何番目か。
(3)下のように、4と9の数字を使わない整数を小さい順に並べる。1,2,3,5,6,7,8,10,11,…このとき、40番目の数を求めよ。
【受験算数】菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちる…【Part2】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈412〉と表す。ただし、このケースには卵は215個までしか入りません。
(1)針が〈412〉となっているとき、何個の卵がケースに落ちたか。
(2)133個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
この動画を見る
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈412〉と表す。ただし、このケースには卵は215個までしか入りません。
(1)針が〈412〉となっているとき、何個の卵がケースに落ちたか。
(2)133個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
【受験算数】菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈243〉と表す。ただし、このケースには卵は124個までしか入らない。
(1)針が〈243〉となっているとき、何個の卵がケースに落ちたか。
(2)79個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
この動画を見る
菊雄君の家では、たくさんの鶏を飼っている。鶏が産んだ卵を集めるケースには、図のような目もりがついていて、Ⅰ、Ⅱ、Ⅲとも0にセットされている。鶏が産んだ卵が下のケースに落ちるたびに、Ⅰの針が1目もり進むようになっている。また、Ⅰの針が1回転すると、Ⅱの針が1目もり進み、Ⅱの針が1回転するとⅢの針が1目もり進む。針が図のようになっているとき、これを〈243〉と表す。ただし、このケースには卵は124個までしか入らない。
(1)針が〈243〉となっているとき、何個の卵がケースに落ちたか。
(2)79個の卵が下のケースに落ちると、針ははじめの〈000〉の状態から、それぞれどの数字を指すか。
【数C】【平面上の曲線】極座標に関して、次の2点を通る直線の極方程式を求めよ(1) A(1,0)、B(2,2π/3)(2) C(2,π/6)、D(4,5π/6)

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標に関して、次の 2 点を通る直線の極方程式を求めよ。
(1) $A(1,0)$、$B(2,\frac{2}{3}\pi)$
(2) $C(2,\frac{\pi}{6})$、$D(4,\frac{5}{6}\pi)$
この動画を見る
極座標に関して、次の 2 点を通る直線の極方程式を求めよ。
(1) $A(1,0)$、$B(2,\frac{2}{3}\pi)$
(2) $C(2,\frac{\pi}{6})$、$D(4,\frac{5}{6}\pi)$
【数C】【平面上の曲線】極座標で表された次の2点P,Q間の距離を求めよ。△OPQの面積を求めよ。(1) P(2,π/3)、Q(3,2π/3) (2) P(4,5π/12)、Q(1、-3π/4)

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標で表された次の 2 点 P、Q 間の距離を求めよ。
また、$\triangle OPQ$ の面積を求めよ。
ただし、O は極とする。
(1) $P(2,\frac{\pi}{3})$、$Q(3,\frac{2}{3}\pi)$
(2) $P(4,\frac{5}{12}\pi)$、$Q(1,-\frac{3}{4}\pi)$
この動画を見る
極座標で表された次の 2 点 P、Q 間の距離を求めよ。
また、$\triangle OPQ$ の面積を求めよ。
ただし、O は極とする。
(1) $P(2,\frac{\pi}{3})$、$Q(3,\frac{2}{3}\pi)$
(2) $P(4,\frac{5}{12}\pi)$、$Q(1,-\frac{3}{4}\pi)$
【数C】【平面上の曲線】2直線 r(√3cosθ+sinθ)=4、r(√3cosθ-sinθ)=2の交点の極座標を求めよ。また、この2直線のなす角を求めよ。

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
直線 $r(\sqrt{3}\cos\theta+\sin\theta)=4$、
$r(\sqrt{3}\cos\theta-\sin\theta)=2$
の交点の極座標を求めよ。
また、この 2 直線のなす角を求めよ。
この動画を見る
直線 $r(\sqrt{3}\cos\theta+\sin\theta)=4$、
$r(\sqrt{3}\cos\theta-\sin\theta)=2$
の交点の極座標を求めよ。
また、この 2 直線のなす角を求めよ。
【数C】【平面上の曲線】極座標に関して、中心が(2,π/6)、半径が√3である円に、極から引いた2本の接線の極方程式求めよ

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#式と曲線
指導講師:
理数個別チャンネル
問題文全文(内容文):
極座標に関して、中心が $(2,\frac{\pi}{6})$、
半径 $\sqrt{3}$ である円に、極から引いた
2 本の接線の極方程式を求めよ。
この動画を見る
極座標に関して、中心が $(2,\frac{\pi}{6})$、
半径 $\sqrt{3}$ である円に、極から引いた
2 本の接線の極方程式を求めよ。
【数Ⅲ】【微分】次の等式を満たす連続関数f(x)を求めよ。f(x)=x²+2+2∫[1→x]tf(t)dt

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす連続関数 $f(x)$ を求めよ。
$f(x)=x^2+2+2\int_1^x f(t)\,dt$
この動画を見る
次の等式を満たす連続関数 $f(x)$ を求めよ。
$f(x)=x^2+2+2\int_1^x f(t)\,dt$
【数Ⅲ】【微分】曲線y=f(x)は原点Oを通りO以外の曲線上の点P(x,y)について、その点における接線の傾きが常に直線OPの傾きの2倍である。この曲線は点A(1,2)を通る。この曲線の方程式を求めよ

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線y=f(x)は原点Oを通り、O以外の曲線上の点P(x,y)については、その点における接線の傾きが常に直線OPの傾きの2倍である。また、この曲線は点A(1,2)を通る。この曲線の方程式を求めよ。
この動画を見る
曲線y=f(x)は原点Oを通り、O以外の曲線上の点P(x,y)については、その点における接線の傾きが常に直線OPの傾きの2倍である。また、この曲線は点A(1,2)を通る。この曲線の方程式を求めよ。
【受験算数】赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚…【Part2】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は350cm²
(2)操作前の記号が(オ,9,5,4)のとき、操作後の記号は(3,2,カ,5)
この動画を見る
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は350cm²
(2)操作前の記号が(オ,9,5,4)のとき、操作後の記号は(3,2,カ,5)
【受験算数】赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚の…

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は225cm²
(2)操作前の記号が(6,オ,3,7)のとき、操作後の記号は(カ,2,1,8)
この動画を見る
赤、白、青、緑の正方形の紙がそれぞれ何枚かあり、正方形の一辺の長さは赤が1cm、白が2cm、青が4cm、緑が8cmです。いま、赤、白、青、緑の正方形の紙がそれぞれ○枚、△枚、◇枚、◎枚のとき、これらの総面積を、記号(○,△,◇,◎)で表すことにする。例えば、赤1枚、白1枚、青1枚、緑1枚のときの総面積は、次のようになる。(1,1,1,1)=1×1×1+2×2×1+4×4×1+8×8×1=85(cm²)
また、紙を取りかえる次の操作を行う。操作:赤4枚は白1枚に、白4枚は青1枚に、青4枚は緑1枚に、それぞれ必ず取りかえる。
次のア,イ,ウ,エ,オ,カを求めよ。
(1)操作後の記号が(ア,イ,ウ,エ)のとき、総面積は225cm²
(2)操作前の記号が(6,オ,3,7)のとき、操作後の記号は(カ,2,1,8)
【数Ⅲ】【微分】yはxの関数とする。次の微分方程式を、与えられたおき換えを利用して解け。(1) dy/dx=y/x+x/y (y/x=u)(2) dy/dx=x+y (x+y=u)

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
$y$ は $x$ の関数とする。次の微分方程式を、
与えられたおき換えを利用して解け。
(1) $\frac{dy}{dx}=\frac{y}{x}+\frac{x}{y}$($\frac{y}{x}=u$)
(2) $\frac{dy}{dx}=x+y$($x+y=u$)
この動画を見る
$y$ は $x$ の関数とする。次の微分方程式を、
与えられたおき換えを利用して解け。
(1) $\frac{dy}{dx}=\frac{y}{x}+\frac{x}{y}$($\frac{y}{x}=u$)
(2) $\frac{dy}{dx}=x+y$($x+y=u$)
【数Ⅲ】【関数と極限】次の方程式の実数解の存在する区間をすべて求めよ。ただし、区間は幅1の開区間とし、その両端は整数値とする。(1) 2x³+3x²-12x-3=0(2) x³+x²-2x-1=0

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式の実数解の存在する区間をすべて求めよ。ただし、区間は幅1の
開区間とし、その両端は整数値とする。
(1) 2x³+3x²-12x-3=0
(2) x³+x²-2x-1=0
この動画を見る
次の方程式の実数解の存在する区間をすべて求めよ。ただし、区間は幅1の
開区間とし、その両端は整数値とする。
(1) 2x³+3x²-12x-3=0
(2) x³+x²-2x-1=0
【数Ⅲ】【関数と極限】関数f(x)が連続でf(0)=-1、f(1)=2、f(2)=1、f(3)=4のとき、方程式f(x)=xは0<x<3の範囲に少なくとも3個の実数解をもつことを示せ。

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
【数Ⅲ】【関数と極限】グラフをかき、その連続性について調べよ。(1) y=lim 1+x/1+xΛ2n(2) y=lim x-1/1+|x|Λn(3) y=lim nsin2x+1/ncos²x+1

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかき、その連続性について調べよ。
(1) $y=\displaystyle \lim_{n\to\infty}\frac{1+x}{1+x^{2n}}$
(2) $y=\displaystyle \lim_{n\to\infty}\frac{x-1}{1+|x|^{n}}$
(3) $y=\displaystyle \lim_{n\to\infty}\frac{n\sin 2x+1}{n\cos^2 x+1}$
この動画を見る
次の関数のグラフをかき、その連続性について調べよ。
(1) $y=\displaystyle \lim_{n\to\infty}\frac{1+x}{1+x^{2n}}$
(2) $y=\displaystyle \lim_{n\to\infty}\frac{x-1}{1+|x|^{n}}$
(3) $y=\displaystyle \lim_{n\to\infty}\frac{n\sin 2x+1}{n\cos^2 x+1}$
【受験算数】下の図のような、文字盤に同じ間隔で1から24までかかれた特殊な時計があります。この時計は、長針は右回りで2時間で1周し、短針は右回りで1日で1周します。0時には、長針も短針も24を指して…

単元:
#算数(中学受験)#速さ#点の移動・時計算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のような、文字盤に同じ間隔で1から24までかかれた特殊な時計があります。この時計は、長針は右回りで2時間で1周し、短針は右回りで1日で1周します。0時には、長針も短針も24を指しています。図が表している時刻は15時5分です。これについて、次の問いに答えなさい。
⑴ 17時のとき、長針と短針が作る小さい方の角度は何度ですか。
⑵ 16時36分のとき、長針と短針が作る小さい方の角度は何度ですか。
⑶ 13時から長針と短針が重なる時刻を調べたとき、3回目に重なるのは何時何分ですか。24時制で答えなさい。
この動画を見る
下の図のような、文字盤に同じ間隔で1から24までかかれた特殊な時計があります。この時計は、長針は右回りで2時間で1周し、短針は右回りで1日で1周します。0時には、長針も短針も24を指しています。図が表している時刻は15時5分です。これについて、次の問いに答えなさい。
⑴ 17時のとき、長針と短針が作る小さい方の角度は何度ですか。
⑵ 16時36分のとき、長針と短針が作る小さい方の角度は何度ですか。
⑶ 13時から長針と短針が重なる時刻を調べたとき、3回目に重なるのは何時何分ですか。24時制で答えなさい。
【受験算数】1辺1mの立方体の箱を地面に置き、高さ2mの電灯によって地面にできる箱の影について考えます。ただし、箱の底の部分は影に含めないものとします。 (図1)のように、箱のかどの真上に電灯がある…
単元:
#算数(中学受験)#平面図形#相似と相似を利用した問題#立体図形#立体図形その他
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
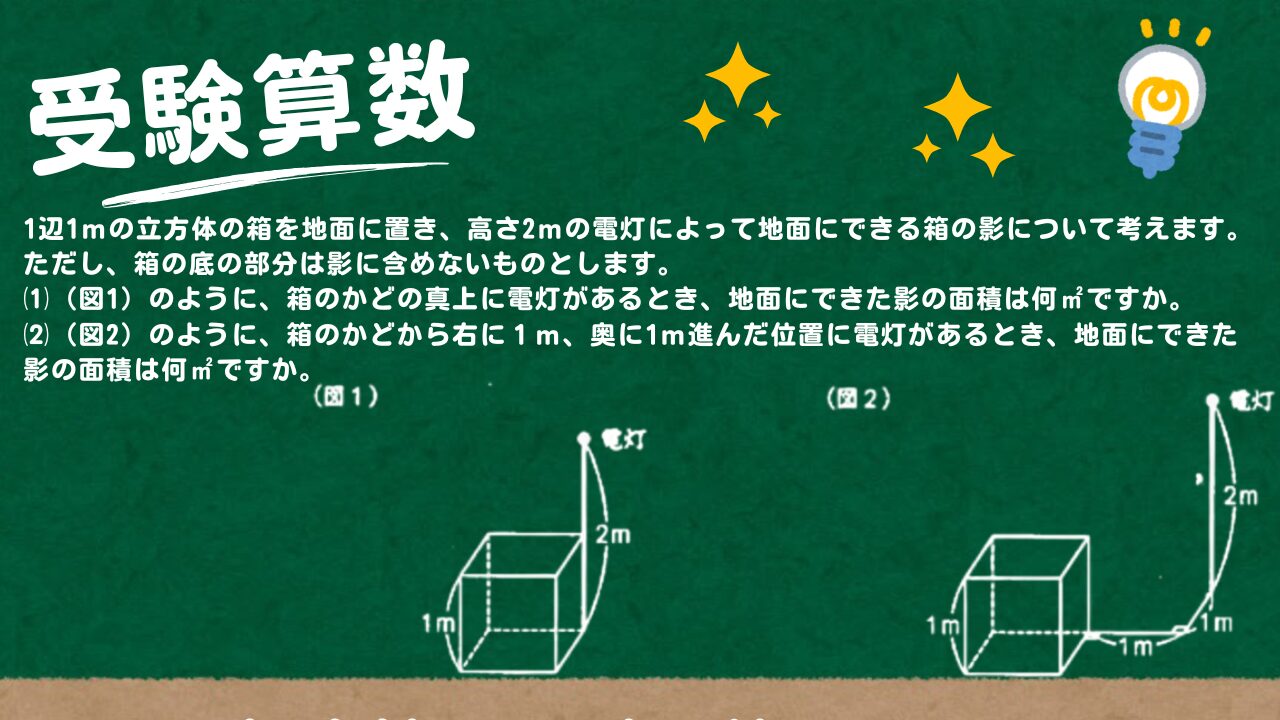
1辺1mの立方体の箱を地面に置き、高さ2mの電灯によって地面にできる箱の影について考えます。ただし、箱の底の部分は影に含めないものとします。また、必要であれば、下の方眼紙を使って考えなさい。
⑴ (図1)のように、箱のかどの真上に電灯があるとき、地面にできた影の面積は何㎡ですか。
⑵ (図2)のように、箱のかどから右に1m、奥に1m進んだ位置に電灯があるとき、地面にできた影の面積は何㎡ですか。
この動画を見る
1辺1mの立方体の箱を地面に置き、高さ2mの電灯によって地面にできる箱の影について考えます。ただし、箱の底の部分は影に含めないものとします。また、必要であれば、下の方眼紙を使って考えなさい。
⑴ (図1)のように、箱のかどの真上に電灯があるとき、地面にできた影の面積は何㎡ですか。
⑵ (図2)のように、箱のかどから右に1m、奥に1m進んだ位置に電灯があるとき、地面にできた影の面積は何㎡ですか。
【数Ⅲ】【関数と極限】無限級数x+x/1+|x|+x/(1+|x|)²+……+x/(1+|x|)Λn-1+……をf(x)とおく。無限級数がすべての実数xに対して収束することを示せ。連続性について調べよ

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
無限級数
$x+\dfrac{x}{1+|x|}+\dfrac{x}{(1+|x|)^2}+\cdots+\dfrac{x}{(1+|x|)^{n-1}}+\cdots$
の和を $f(x)$ とおく。
この無限級数がすべての実数 $x$ に対して収束することを示せ。
また、関数 $y=f(x)$ のグラフをかき、
その連続性について調べよ。
この動画を見る
無限級数
$x+\dfrac{x}{1+|x|}+\dfrac{x}{(1+|x|)^2}+\cdots+\dfrac{x}{(1+|x|)^{n-1}}+\cdots$
の和を $f(x)$ とおく。
この無限級数がすべての実数 $x$ に対して収束することを示せ。
また、関数 $y=f(x)$ のグラフをかき、
その連続性について調べよ。
【数Ⅲ】【関数と極限】次の関数f(x)において、定義されないxの値、不連続であるxの値をいえ。(1) f(x)=x²-2x-3/x-3(2) f(x)=x³/|x|(3) f(x)=[|cosx|]

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数 f(x) において、定義されない x の値、
不連続である x の値をいえ。
また、それらの x の値で、関数の値を改めて定義し、
すべての実数 x で連続になるようにせよ。
(1) $f(x)=\frac{x^2-2x-3}{x-3}$
(2) $f(x)=\frac{x^3}{|x|}$
(3) $f(x)=[[ \cos x ]]$
この動画を見る
次の関数 f(x) において、定義されない x の値、
不連続である x の値をいえ。
また、それらの x の値で、関数の値を改めて定義し、
すべての実数 x で連続になるようにせよ。
(1) $f(x)=\frac{x^2-2x-3}{x-3}$
(2) $f(x)=\frac{x^3}{|x|}$
(3) $f(x)=[[ \cos x ]]$
【数Ⅲ】【関数と極限】次の関数f(x)の定義域をいえ。また、定義域における連続性について調べよ。(1) f(x)=x+1/x²-1(2) f(x)=x-[x]

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数 f(x) の定義域をいえ。
また、定義域における連続性について調べよ。
(1) $f(x)=\dfrac{x+1}{x^2-1}$
(2) $f(x)=x-[x]$
この動画を見る
次の関数 f(x) の定義域をいえ。
また、定義域における連続性について調べよ。
(1) $f(x)=\dfrac{x+1}{x^2-1}$
(2) $f(x)=x-[x]$
凸レンズ:焦点距離 20cmの凸レンズの前方30cmの位置に、大きさ4.0cmの物体を置いた。(1) レンズによる物体の像の位置、大きさを求めよ。また、像は実像か虚像か、正立か倒立かを答えよ。…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
焦点距離 20cmの凸レンズの前方30cmの位置に、大きさ4.0cmの物体を置いた。
(1) レンズによる物体の像の位置、大きさを求めよ。また、像は実像か虚像か、正立か倒立かを答えよ。
(2) レンズの上半分を紙で覆い、光をさえぎったとき、物体の像はどのようになるか。
この動画を見る
焦点距離 20cmの凸レンズの前方30cmの位置に、大きさ4.0cmの物体を置いた。
(1) レンズによる物体の像の位置、大きさを求めよ。また、像は実像か虚像か、正立か倒立かを答えよ。
(2) レンズの上半分を紙で覆い、光をさえぎったとき、物体の像はどのようになるか。
【受験算数】秒速20mの急行列車が、ホームを24秒で通過しました。その後、秒速28mの特急列車がホームを18秒で通過し、先を走る急行列車に追いついてから追いこすまでに48秒かかりました。ホームの長さは

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
秒速20mの急行列車が、ホームを24秒で通過しました。その後、秒速28mの特急列車がホームを18秒で通過し、先を走る急行列車に追いついてから追いこすまでに48秒かかりました。ホームの長さは何mですか。
この動画を見る
秒速20mの急行列車が、ホームを24秒で通過しました。その後、秒速28mの特急列車がホームを18秒で通過し、先を走る急行列車に追いついてから追いこすまでに48秒かかりました。ホームの長さは何mですか。
【高校化学】次の(ア)~(工)の気体10gずつ取ったとき、同温同圧で最も体積が大きいものを選べ(ア)水素(イ) 窒素 (ウ) メタン (エ) プロパン

単元:
#化学#化学理論#気体の性質#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(ア)~(工)の気体10gずつ取ったとき、
同温同圧で最も体積が大きいものを選べ
(ア)水素(イ) 窒素 (ウ) メタン (エ) プロパン
この動画を見る
次の(ア)~(工)の気体10gずつ取ったとき、
同温同圧で最も体積が大きいものを選べ
(ア)水素(イ) 窒素 (ウ) メタン (エ) プロパン
【高校化学】(1) 質量パーセントを求めよ(ア)SO₂ 【S】(イ) C₆H₁₂O₆ 【C】(2)ある金属元素Mの酸化物MO₂17.4gを還元するとMの単体が11.0g得られた金属元素の原子量を求めよ





