 整数の性質
整数の性質
 整数の性質
整数の性質
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数である.これを解け.
$m^6+295=2^n$
この動画を見る
$m,n$は自然数である.これを解け.
$m^6+295=2^n$
ユークリッドで一次不定方程式解くステップ、歌にして説明してみた【覚えやすさに全振り】もちろん解説もします。

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
ユークリッドで一次不定方程式解くステップ解説動画です
この動画を見る
ユークリッドで一次不定方程式解くステップ解説動画です
東大(類題)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-6x-1=0$の2つの解を$\alpha,\beta(\alpha \gt \beta)$とする.
$\alpha^{1002}$の1の位を求めよ.
東大(類)2003過去問
この動画を見る
$x^2-6x-1=0$の2つの解を$\alpha,\beta(\alpha \gt \beta)$とする.
$\alpha^{1002}$の1の位を求めよ.
東大(類)2003過去問
京都府採用試験数学【2016】

単元:
#数Ⅰ#数A#数Ⅱ#数と式#場合の数と確率#平面上のベクトル#複素数平面#図形と計量#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#場合の数#確率#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#積分とその応用#複素数平面#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
この動画を見る
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
*図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
息抜き整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n!+8=2^k$
自然数$(n,k)$をすべて求めよ.
この動画を見る
$n!+8=2^k$
自然数$(n,k)$をすべて求めよ.
約数の総積 数学オリンピック予選

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
正の約数すべての積が$24^{240}$とんる自然数をすべて求めよ.
数学オリンピック過去問
この動画を見る
正の約数すべての積が$24^{240}$とんる自然数をすべて求めよ.
数学オリンピック過去問
ユークリッドの互除法、死ぬほど覚えられない人へ。急ぎの人は【4:26まで】見て。(筆算の「形」を絵描き歌で覚えるのが一番早いし忘れない)【数学

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
ユークリッドの互除法についての解説動画です
767と921の最大公約数は?
この動画を見る
ユークリッドの互除法についての解説動画です
767と921の最大公約数は?
数1

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数である.
$(m,n)$を求めよ.
①$m^2-n^2-2n=21$
②$m^3+n^3-3mn=3$
この動画を見る
$m,n$は自然数である.
$(m,n)$を求めよ.
①$m^2-n^2-2n=21$
②$m^3+n^3-3mn=3$
最小公倍数 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n,A,B$を自然数とする.
$A$と$B(1\leqq A\lt B)$の最小公倍数は$10^n$である.
$(A,B)$の組数を求めよ.
この動画を見る
$n,A,B$を自然数とする.
$A$と$B(1\leqq A\lt B)$の最小公倍数は$10^n$である.
$(A,B)$の組数を求めよ.
整数問題 合同式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$7^m-1032=n^2$,自然数$(m,n)$をすべて求めよ.
この動画を見る
$7^m-1032=n^2$,自然数$(m,n)$をすべて求めよ.
整数 九州大

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを示せ.
2014九州大過去問
この動画を見る
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを示せ.
2014九州大過去問
N進法 整数問題

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
7進法で表された8桁の数$A123456B$が4の倍数となる$(A,B)$の組をすべて求めよ.
この動画を見る
7進法で表された8桁の数$A123456B$が4の倍数となる$(A,B)$の組をすべて求めよ.
合同式 数学的帰納法 東工大

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数学的帰納法#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$79^n+(-1)^n.2^{6n-5}$は必ずある自然数であるとき,$m$の倍数と最大値を求めよ.
東工大過去問
この動画を見る
$n$は自然数である.
$79^n+(-1)^n.2^{6n-5}$は必ずある自然数であるとき,$m$の倍数と最大値を求めよ.
東工大過去問
合同式の基本 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1\times 3\times 5\times 7\times・・・・・・\times 999$を$16$で割った余りを求めよ.
この動画を見る
$1\times 3\times 5\times 7\times・・・・・・\times 999$を$16$で割った余りを求めよ.
整数問題 一橋大(類)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての自然数$n$について$7^n+an+b$が$36$の倍数となる$36$以下の自然数$a,b$を求めよ.
一橋大(類)過去問
この動画を見る
すべての自然数$n$について$7^n+an+b$が$36$の倍数となる$36$以下の自然数$a,b$を求めよ.
一橋大(類)過去問
整数問題 九州大

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$n$が偶数なら$2^n-1$は3の倍数を示せ.
(2)$2^m+1$と$2^m-1$は互いに素($m$は自然数)を示せ.
(3)$p,q$は異なる素数$2^{p-1}-1=pq^2$である.
$(p,q)$をすべて求めよ.
2015九州大過去問
この動画を見る
(1)$n$が偶数なら$2^n-1$は3の倍数を示せ.
(2)$2^m+1$と$2^m-1$は互いに素($m$は自然数)を示せ.
(3)$p,q$は異なる素数$2^{p-1}-1=pq^2$である.
$(p,q)$をすべて求めよ.
2015九州大過去問
整数問題 慶應義塾大
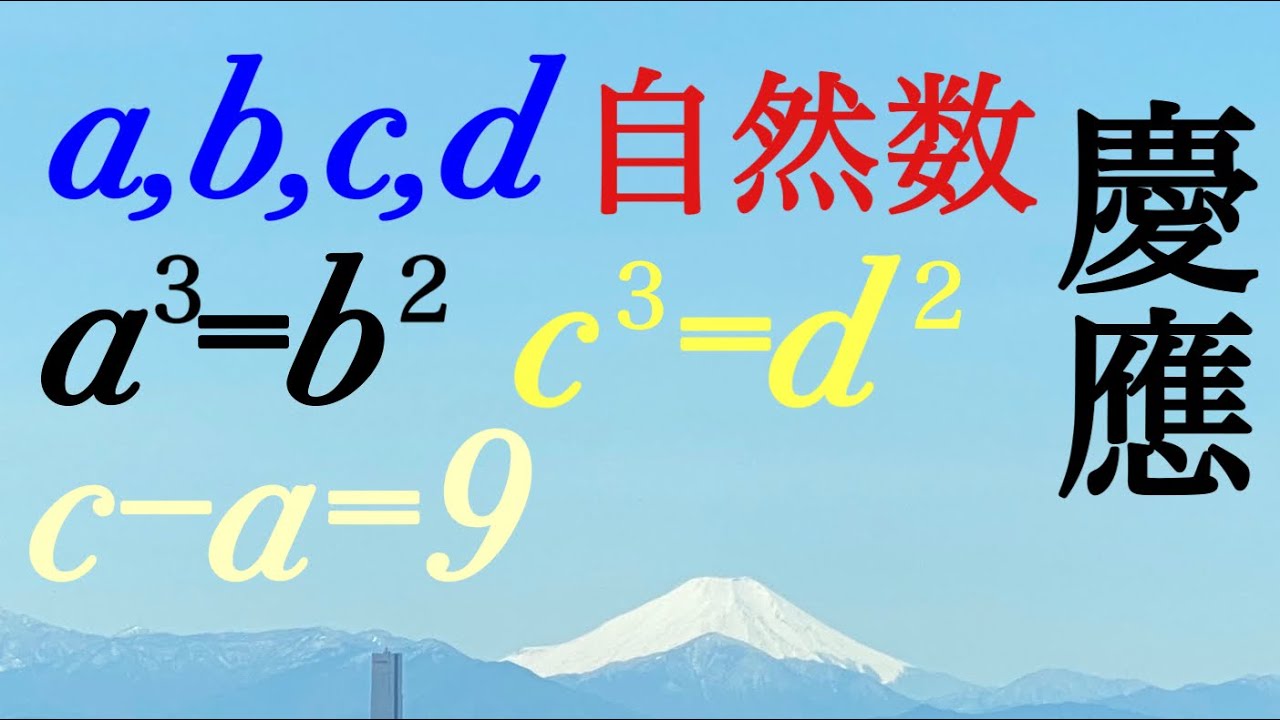
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c,d$は自然数である.これを解け.
$a^3=b^2,c^3=d^2,c-a=9$
2020慶應大過去問
この動画を見る
$a,b,c,d$は自然数である.これを解け.
$a^3=b^2,c^3=d^2,c-a=9$
2020慶應大過去問
対称式 名古屋市立大

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a+b+c-2,ab+bc+ca=3,abc=2$である.
$a^5+b^5+c^5$の値を求めよ.
2012名古屋市立大過去問
この動画を見る
$a+b+c-2,ab+bc+ca=3,abc=2$である.
$a^5+b^5+c^5$の値を求めよ.
2012名古屋市立大過去問
合同式 千葉大

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z,n$は自然数である.$x^2=7^{2n}(y^2+10z^2)$である.
(1)平方数を3で割った余りは0か1であることを示せ.
(2)$yz$は3の倍数であることを示せ.
(3)$y,z$が共に素数のとき,$x$を$n$を用いて表せ.
2003千葉大過去問
この動画を見る
$x,y,z,n$は自然数である.$x^2=7^{2n}(y^2+10z^2)$である.
(1)平方数を3で割った余りは0か1であることを示せ.
(2)$yz$は3の倍数であることを示せ.
(3)$y,z$が共に素数のとき,$x$を$n$を用いて表せ.
2003千葉大過去問
合同式の基本 灘中

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
各位の数が全て異なる$7$桁の$11$の倍数で最大なものを求めよ.
2011灘中(改)過去問
この動画を見る
各位の数が全て異なる$7$桁の$11$の倍数で最大なものを求めよ.
2011灘中(改)過去問
青山学院大 2数の積の総和

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$1,2…n$の中から異なる2つの数をとって積をつくるとき、それらの積の総和を求めよ
$(n \geqq 2)$
出典:2005年青山学院大学 過去問
この動画を見る
自然数$1,2…n$の中から異なる2つの数をとって積をつくるとき、それらの積の総和を求めよ
$(n \geqq 2)$
出典:2005年青山学院大学 過去問
千葉大 2次方程式の解 整数問題

単元:
#数Ⅰ#数A#2次関数#2次関数とグラフ#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$素数
$Px^2+(5-P^2)x-3P=0$が整数解をもつ$P$の値を求めよ
出典:2003年千葉大学 過去問
この動画を見る
$P$素数
$Px^2+(5-P^2)x-3P=0$が整数解をもつ$P$の値を求めよ
出典:2003年千葉大学 過去問
整数 約数の個数・総和

東大受験芸人たわしさん解説 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^5-n$が30の倍数であることを示せ
出典:弘前大学 過去問
この動画を見る
$n^5-n$が30の倍数であることを示せ
出典:弘前大学 過去問
群馬大(医)

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$log_{5832}n$が有理数で$\displaystyle \frac{1}{2} \lt log_{5832}n \lt 1$である自然数$n$を求めよ
出典:群馬大学医学部 過去問
この動画を見る
$log_{5832}n$が有理数で$\displaystyle \frac{1}{2} \lt log_{5832}n \lt 1$である自然数$n$を求めよ
出典:群馬大学医学部 過去問
神戸大 N進法
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
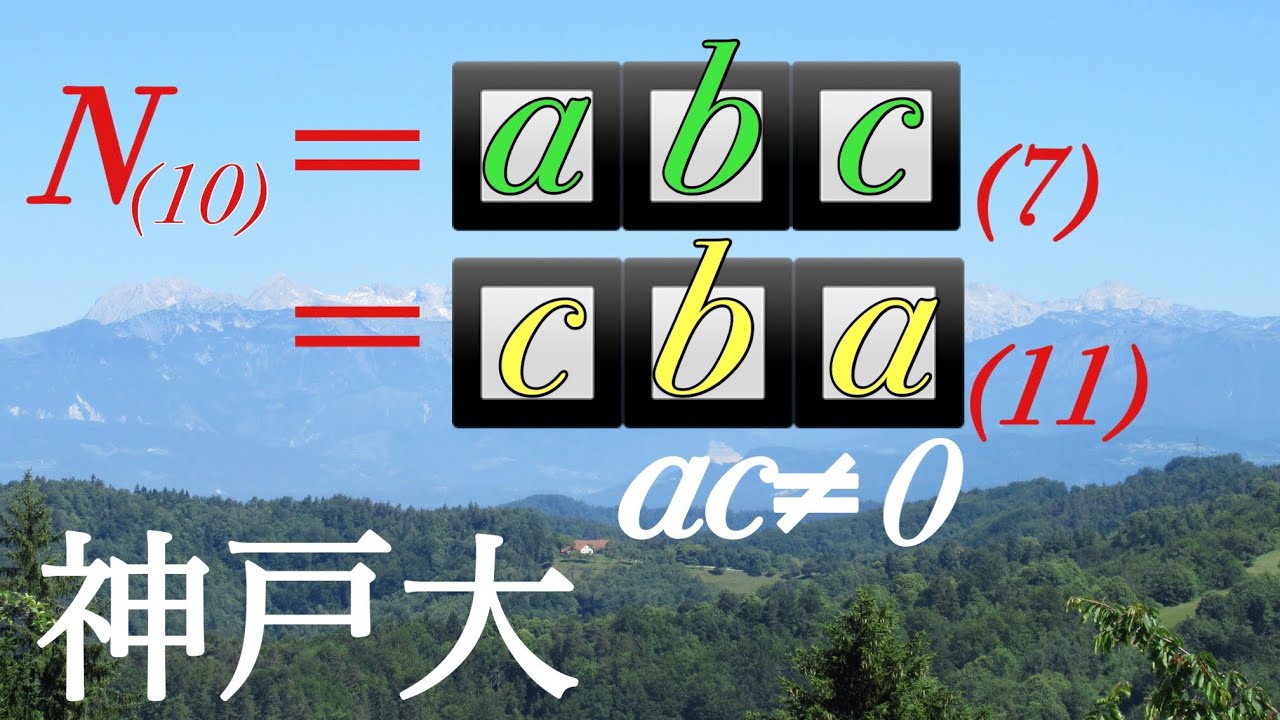
$N_{(10)}$を7進法、11進法で表すといずれも3ケタになり、数字の並びが反対であった。
$N_{(10)}$を求めよ
$ac \neq 0$
出典:1968年神戸大学 過去問
この動画を見る
$N_{(10)}$を7進法、11進法で表すといずれも3ケタになり、数字の並びが反対であった。
$N_{(10)}$を求めよ
$ac \neq 0$
出典:1968年神戸大学 過去問
帝京大(医)整数の性質

単元:
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$N=2^{20}7^{10}$
(1)
$N$を5で割った余りを求めよ
(2)
$N$の正の約数
全部の積を$M$
$log_NM$の値を求めよ
出典:2005年帝京大学医学部 過去問
この動画を見る
$N=2^{20}7^{10}$
(1)
$N$を5で割った余りを求めよ
(2)
$N$の正の約数
全部の積を$M$
$log_NM$の値を求めよ
出典:2005年帝京大学医学部 過去問
場合の数

単元:
#数A#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n,x,y,z$は$0$以上の整数
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか求めよ
この動画を見る
$n,x,y,z$は$0$以上の整数
$2x+y+z=n$を満たす$(x,y,z)$は何組あるか求めよ
整数問題 二項定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2^{3^n}+1$は3で何回割り切れるか求めよ。$(n$自然数$)$
この動画を見る
$2^{3^n}+1$は3で何回割り切れるか求めよ。$(n$自然数$)$
一橋大 整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$自然数
$3p^3-p^2q-pq^2+3q^3=2013$を満たす$(p,q)$すべて求めよ
出典:一橋大学 過去問
この動画を見る
$p,q$自然数
$3p^3-p^2q-pq^2+3q^3=2013$を満たす$(p,q)$すべて求めよ
出典:一橋大学 過去問
