 式と証明
式と証明
 式と証明
式と証明
福田の数学〜慶應義塾大学2024環境情報学部第1問(1)〜相加平均と相乗平均の関係

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
この動画を見る
$x,y$ を正の実数とするとき、$\displaystyle 27x + \frac{3x}{y} + \frac{2y}{x}$ は $\displaystyle x=\frac{\fbox{アイ}}{\fbox{ウエ}},$ $\displaystyle y= \frac{\fbox{オカ}}{\fbox{キク}}$ において最小値 $\fbox{ケコ}$ をとる。
福田のおもしろ数学288〜三角関数に関する不等式の証明

単元:
#数Ⅱ#式と証明#三角関数#整式の除法・分数式・二項定理#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
この動画を見る
$sin^n2x+(sin^xx-cos^nx)^2\leqq1$を証明して下さい。
福田のおもしろ数学285〜(1+1/n)^(n+1)が減少数列である証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$
b_{n}=(1 + \frac{1}{n})^{n+1}
\
で定まる数列 \{ b_{n} \}は減少数列であることを示せ。
$
この動画を見る
$
b_{n}=(1 + \frac{1}{n})^{n+1}
\
で定まる数列 \{ b_{n} \}は減少数列であることを示せ。
$
福田のおもしろ数学283〜関数不等式を満たす関数を求める

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x$、$y$、$z$に対して
$f(x+y)+f(y+z)+f(z+x) \geqq 3 f(x+2y+3z)$
が成り立つような実数値をとる関数 $f(x)$をすべて求めよ。
この動画を見る
任意の実数$x$、$y$、$z$に対して
$f(x+y)+f(y+z)+f(z+x) \geqq 3 f(x+2y+3z)$
が成り立つような実数値をとる関数 $f(x)$をすべて求めよ。
福田のおもしろ数学279〜関数方程式から関数の値を計算する問題

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
任意の実数$x$に対して$f(x)+f(x-1)=x^2$が成り立ち、$f(19)=94$のとき$f(94)$の値は?
この動画を見る
任意の実数$x$に対して$f(x)+f(x-1)=x^2$が成り立ち、$f(19)=94$のとき$f(94)$の値は?
福田のおもしろ数学277〜ガウス記号の等式の証明

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
この動画を見る
$n$は正の整数とする。
$[\sqrt{n}+\sqrt{n+1}]=[\sqrt{ 4n+2 }]$であることを証明して下さい。
$[n]$は$x$を超えない最大の整数を表します。
福田のおもしろ数学275〜分母の違う項がたくさん並んだ方程式の解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
この動画を見る
次の方程式を満たす$x$を求めて下さい。
$\frac{x-2020}{1}+\frac{x-2019}{2}+\cdots+\frac{x-2000}{21} = \frac{x-1}{2020}+\frac{x-2}{2019}+\cdots+\frac{x-21}{2000} $
3次不等式を解け

福田のおもしろ数学257〜3変数の不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c>0$, $abc=1$ のとき
\begin{equation*}
\left(a-1+\frac{1}{b}\right) \left(b-1+\frac{1}{c}\right) \left(c-1+\frac{1}{a}\right) \leq 1
\end{equation*}
を証明して下さい。
この動画を見る
$a,b,c>0$, $abc=1$ のとき
\begin{equation*}
\left(a-1+\frac{1}{b}\right) \left(b-1+\frac{1}{c}\right) \left(c-1+\frac{1}{a}\right) \leq 1
\end{equation*}
を証明して下さい。
よくある方程式
福田のおもしろ数学251〜条件付き等式の証明問題

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2 + b^2 = 1 \\
c^2+d^2=1\\
ac + bd = 0
\end{array}
\right.
\end{eqnarray}
ならば
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2 + c^2 = 1 \\
b^2+d^2=1\\
ab + cd = 0
\end{array}
\right.
\end{eqnarray}
が成り立つことを証明せよ。
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2 + b^2 = 1 \\
c^2+d^2=1\\
ac + bd = 0
\end{array}
\right.
\end{eqnarray}
ならば
\begin{eqnarray}
\left\{
\begin{array}{l}
a^2 + c^2 = 1 \\
b^2+d^2=1\\
ab + cd = 0
\end{array}
\right.
\end{eqnarray}
が成り立つことを証明せよ。
福田のおもしろ数学250〜2つの数の大小判定

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{1999}+\sqrt{9999}$ と$\sqrt{2000}+\sqrt{9998}$ の大小を比較してください。
この動画を見る
$\sqrt{1999}+\sqrt{9999}$ と$\sqrt{2000}+\sqrt{9998}$ の大小を比較してください。
福田のおもしろ数学242〜複雑な無理方程式の解

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x=2+\sqrt{2+\sqrt{2+\sqrt{x}}}$を満たす$x$は?
この動画を見る
$x=2+\sqrt{2+\sqrt{2+\sqrt{x}}}$を満たす$x$は?
大学入試問題#920「工夫しがいがある問題」

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{x^4+x^2+1}{x^3-1}(x \gt 1)$
出典:1963年 一橋大学
この動画を見る
$f(x)=\displaystyle \frac{x^4+x^2+1}{x^3-1}(x \gt 1)$
出典:1963年 一橋大学
福田のおもしろ数学241〜e^πとπ^eの大小

大学入試問題#919「昔は落ち着いた問題」
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
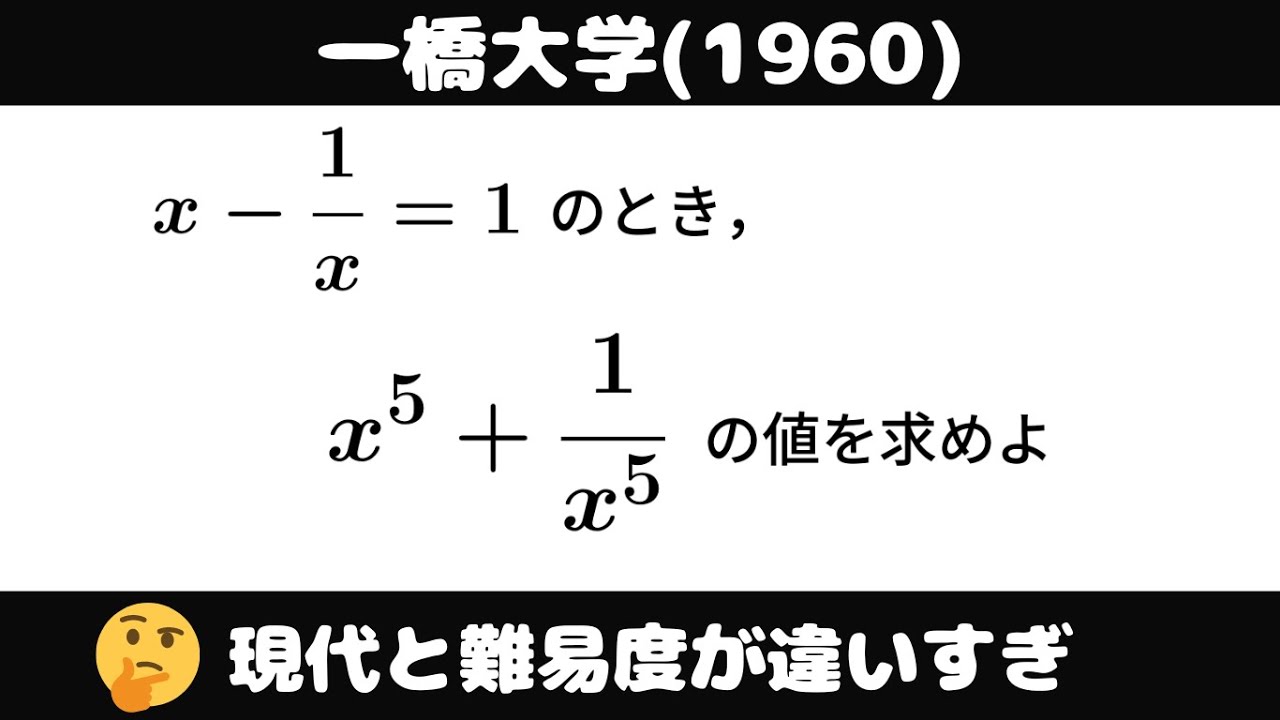
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
この動画を見る
$x-\displaystyle \frac{1}{x}=1$のとき、
$x^5+\displaystyle \frac{1}{x^5}$の値を求めよ。
出典:一橋大(1960)
福田のおもしろ数学240〜e^πが22より大きい証明

#自治医科大学2024#式変形_21#元高校教員

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算(整式・展開・因数分解)#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
この動画を見る
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典:自治医科大学 式変形問題
不等式の証明

福田の数学〜浜松医科大学2024医学部第1問〜等式と不等式の証明とタンジェントの加法定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
この動画を見る
以下の問いに答えよ。
(1) $a$, $b$, $c$ を正の実数とする。このとき、不等式
$a^2b^2+b^2c^2+c^2a^2 \geqq abc(a+b+c)$
を証明せよ。また、等号が成り立つときの$a$, $b$, $c$ の条件を求めよ。
(2) 鋭角三角形の3つの内角を$A$, $B$, $C$とおく。以下の問いに答えよ。
(a)等式
$\tan A+\tan B+\tan C=\tan A\tan B\tan C$
を証明せよ。
(b)不等式
$\displaystyle \frac{1}{\tan A}+\displaystyle \frac{1}{\tan B}+\displaystyle \frac{1}{\tan C} \geqq\sqrt{ 3 }$
を証明せよ。また、等号が成り立つときの鋭角三角形の条件を求めよ。
福田のおもしろ数学222〜条件付きの不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \geq b \geq c, \, x \geq y \geq z, \, x+y+z=0$ のとき、$ax+by+cz \geq 0$ を示せ。
この動画を見る
$a \geq b \geq c, \, x \geq y \geq z, \, x+y+z=0$ のとき、$ax+by+cz \geq 0$ を示せ。
分数式の計算
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\dfrac{1}{x}+\dfrac{1}{x^2-x}=$?
この動画を見る
$\dfrac{1}{x}+\dfrac{1}{x^2-x}=$?
福田のおもしろ数学215〜三平方の定理が成り立つ左辺の二項のどちらか一方は4の倍数である証明

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
この動画を見る
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
福田の数学〜立教大学2024年経済学部第1問(2)〜恒等式の未定係数を決定する方法

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
この動画を見る
等式$\frac{3x^2-x+4}{(x+1)^3}=\frac{a}{(z+1)^3}+\frac{b}{(x+1)^2}+\frac{c}{x+1}$が$x$についての恒等式となるような定数$a, b, c$は$a=\fbox{ウ}, b=\fbox{エ}, c=\fbox{オ}$である。
これ意味わかる?

【保存版】相加平均・相乗平均の覚え方

単元:
#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#その他#数学(高校生)#参考書紹介
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
この動画を見る
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
式の値

福田のおもしろ数学176〜ルートが無限に重なる等式の証明

単元:
#数Ⅱ#式と証明#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
この動画を見る
$\sqrt{x\sqrt{x\sqrt{...}}}$=$x$ を証明してください。ただし$x$は正の実数とする。
福田のおもしろ数学168〜2の100!乗と2の100乗の階乗の大小

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$2^{100!}$と$(2^{100})!$ の大小を比較してせよ。
この動画を見る
$2^{100!}$と$(2^{100})!$ の大小を比較してせよ。
式の値
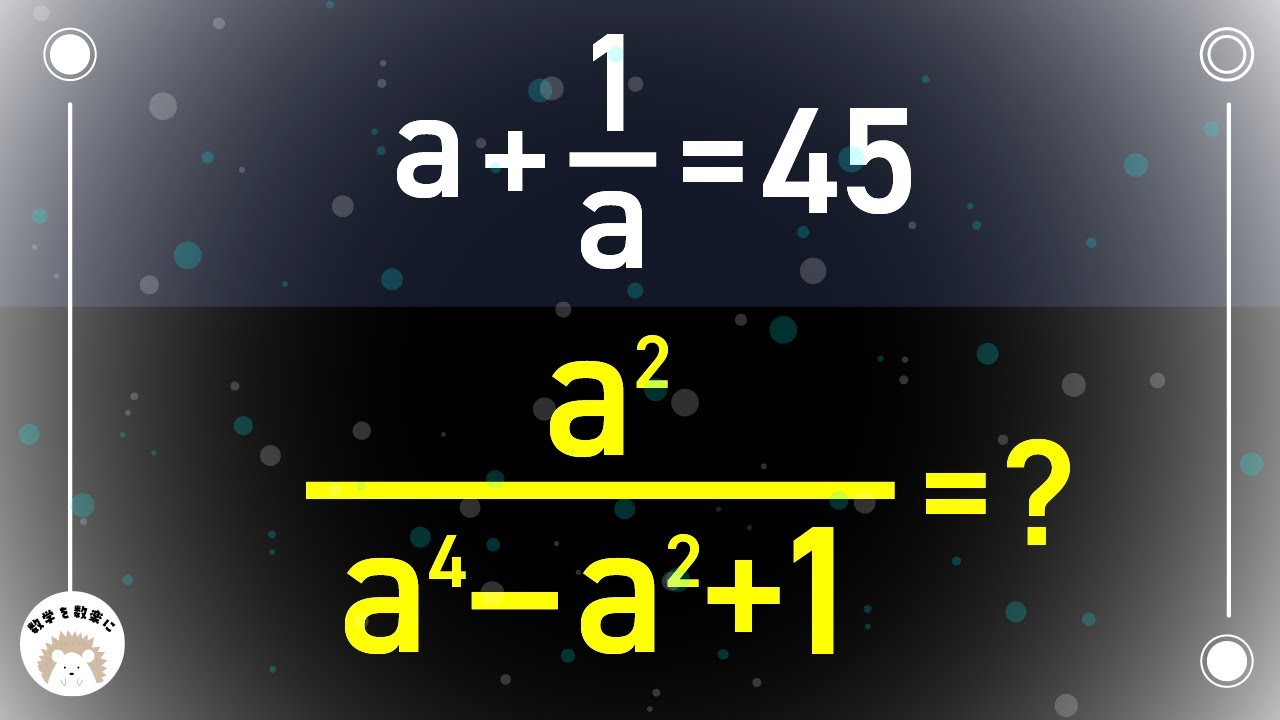
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+\displaystyle \frac{1}{a}=45$のとき、
$\displaystyle \frac{a^2}{a^4-a^2+1}=?$
この動画を見る
$a+\displaystyle \frac{1}{a}=45$のとき、
$\displaystyle \frac{a^2}{a^4-a^2+1}=?$
