 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
大学入試問題#817「難易度の高い詰将棋!大局観が大事!」 #東京医科歯科大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sqrt{ \sin\ 2x }} dx$
出典:2024年東京医科歯科大学
#上智大学(2016) #ウォリス積分 #定積分 #Shorts
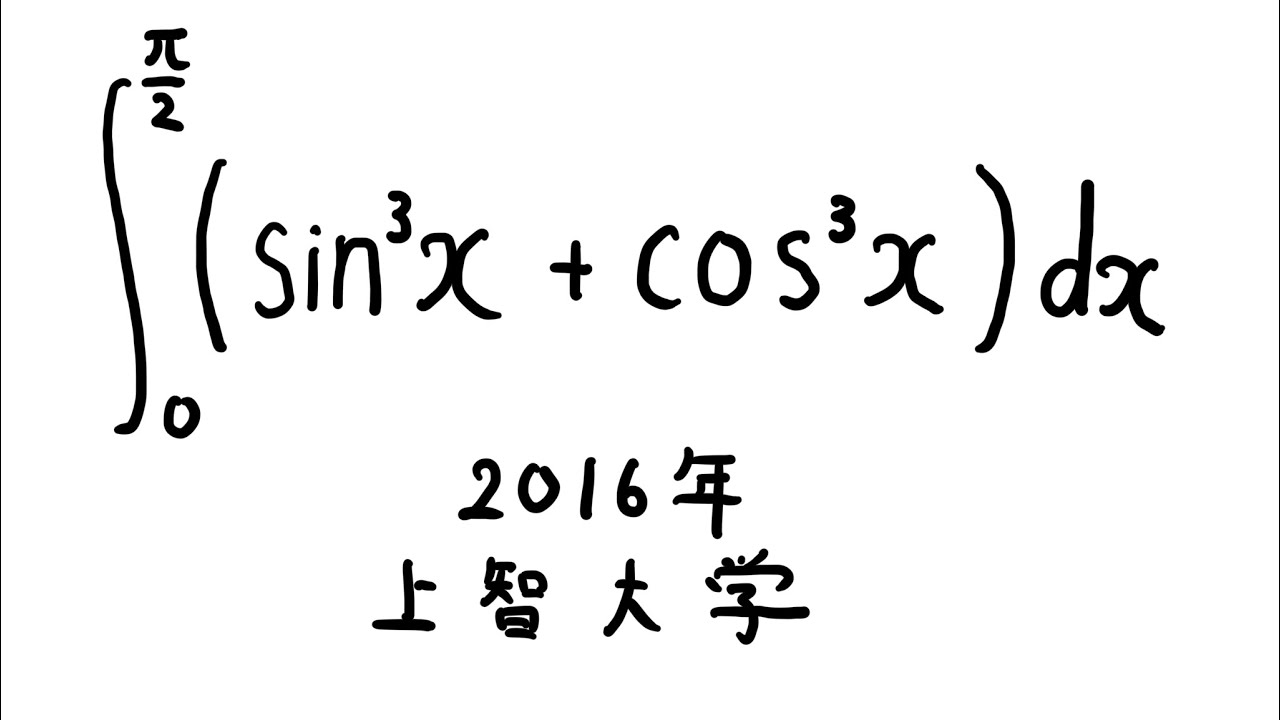
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#上智大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (\sin^3x+\cos^3x) dx$
出典:2016年上智大学
#筑波大学(2018) #定積分 #Shorts
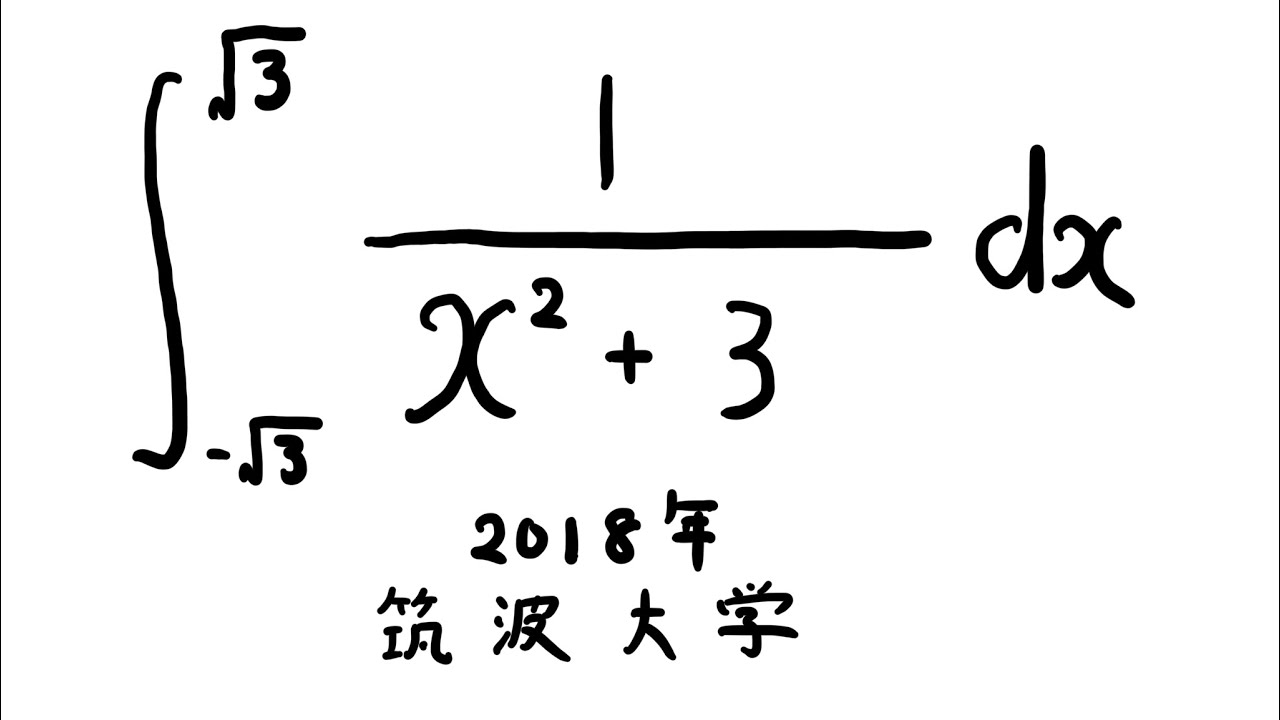
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{1}{x^2+3} dx$
出典:2018年筑波大学
福田の数学〜早稲田大学2024年理工学部第1問〜円の接線で出来る図形の面積の最小
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
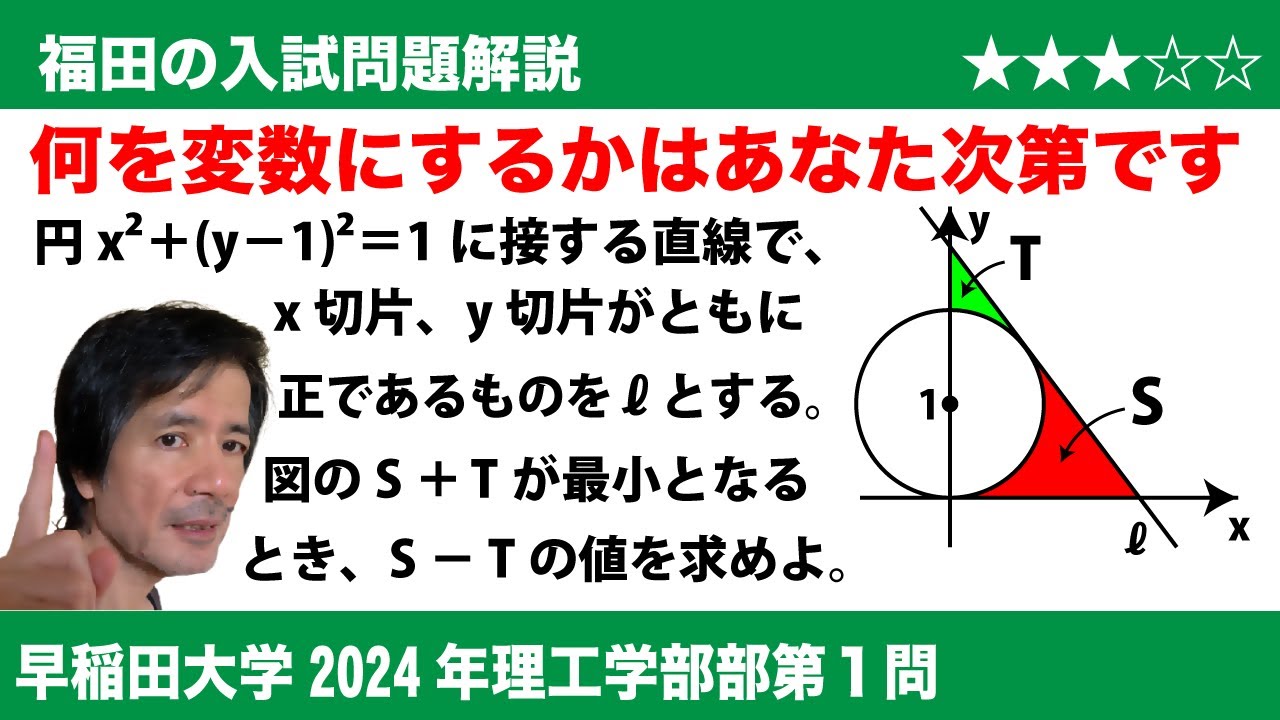
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
福田の数学〜早稲田大学2024年人間科学部第4問〜関数の増減と接線の傾きの長さ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
この動画を見る
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
福田のおもしろ数学126〜条件付き最大値の問題

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
この動画を見る
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
大学入試問題#803「マジで気合い!」 #大阪市立大学(2000) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
福田のおもしろ数学123〜どうして積分すると面積が求まるのでしょう?
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
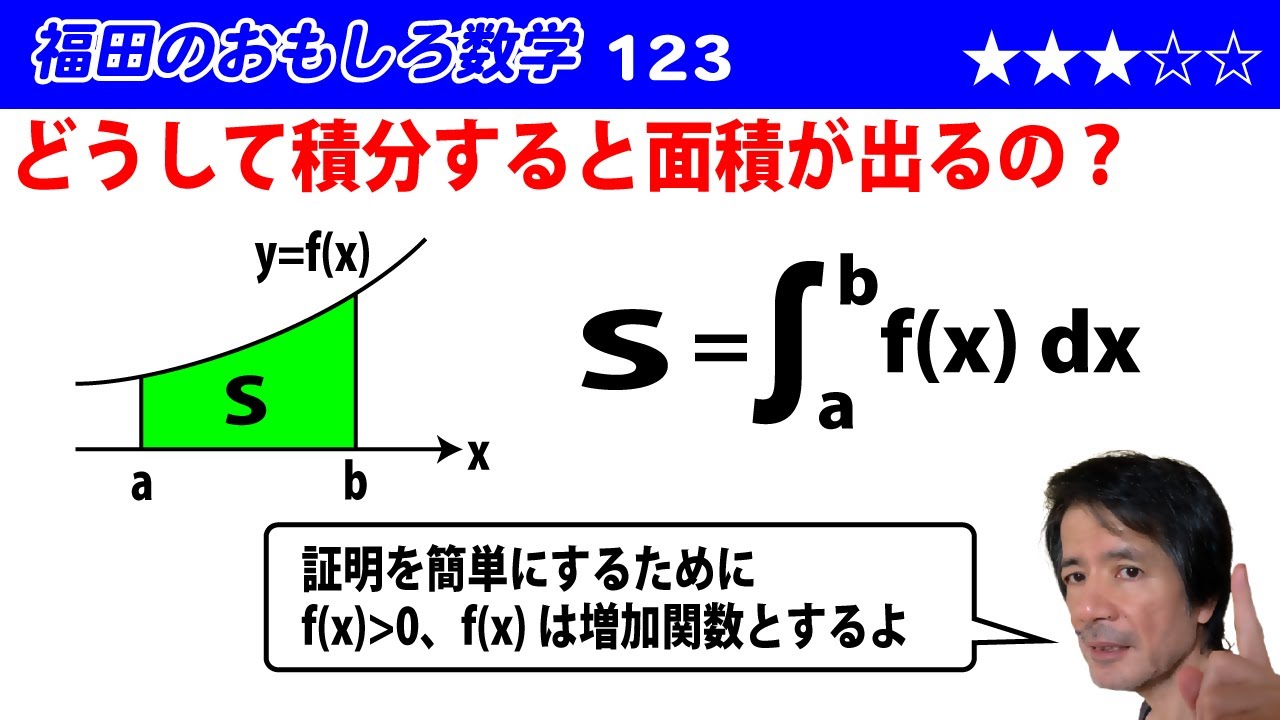
$f(x)$は常に正の値をとる連続な増加関数とする。このとき$y$=$f(x)$のグラフと$x$軸、直線$x$=$a$, $x$=$b$で囲まれる部分の面積を$S$とすると$S$=$\displaystyle\int_a^bf(x)dx$であることを証明せよ。
この動画を見る
$f(x)$は常に正の値をとる連続な増加関数とする。このとき$y$=$f(x)$のグラフと$x$軸、直線$x$=$a$, $x$=$b$で囲まれる部分の面積を$S$とすると$S$=$\displaystyle\int_a^bf(x)dx$であることを証明せよ。
福田の数学〜一橋大学2024年文系第2問〜2つの放物線が共有点で接線直交する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
大学入試問題#799「もう詰んでます!」 #大阪公立大学(2024) #定積分 #King_property

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪公立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
大学入試問題#797「たぶん部分積分でもいけそう」 #名古屋工業大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#名古屋工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
この動画を見る
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
大学入試問題#796「解法は、ほぼ1択か」 #横浜国立大学(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
#会津大学(2015) #定積分 #Shorts
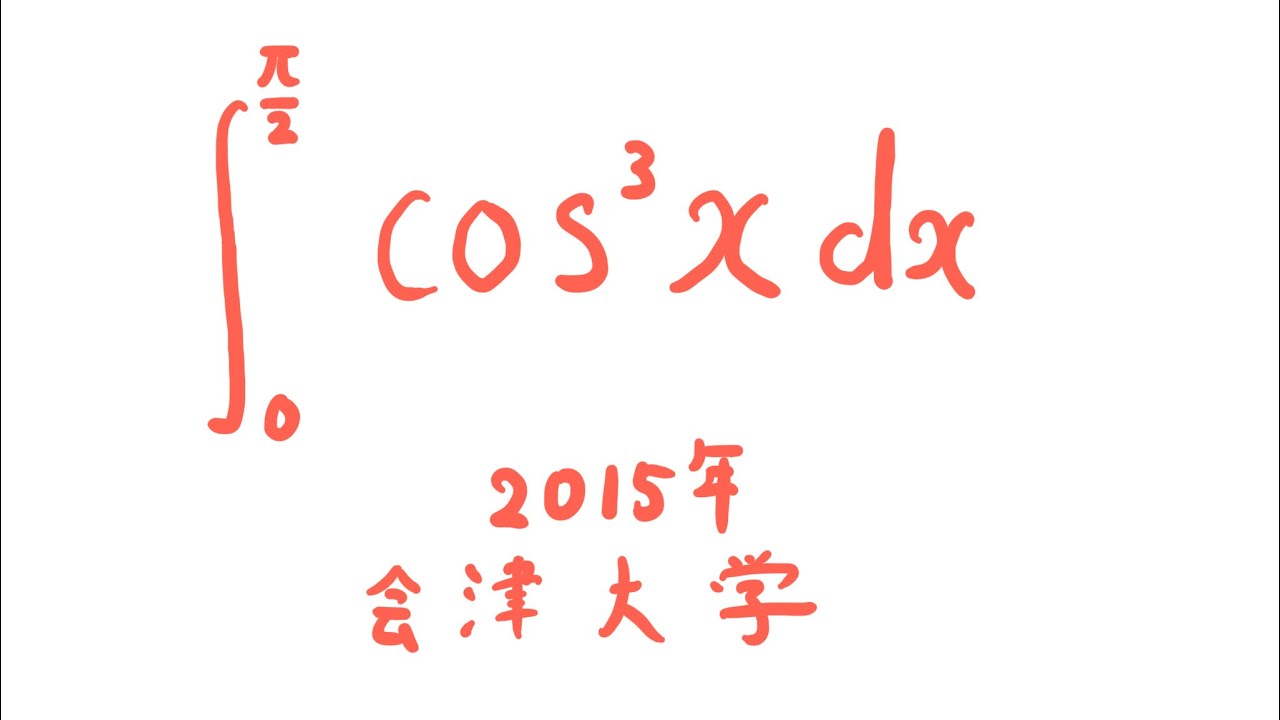
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^3x\ dx$
出典:2015年会津大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos^3x\ dx$
出典:2015年会津大学
#日本工業大学(2021) #定積分 #Shorts
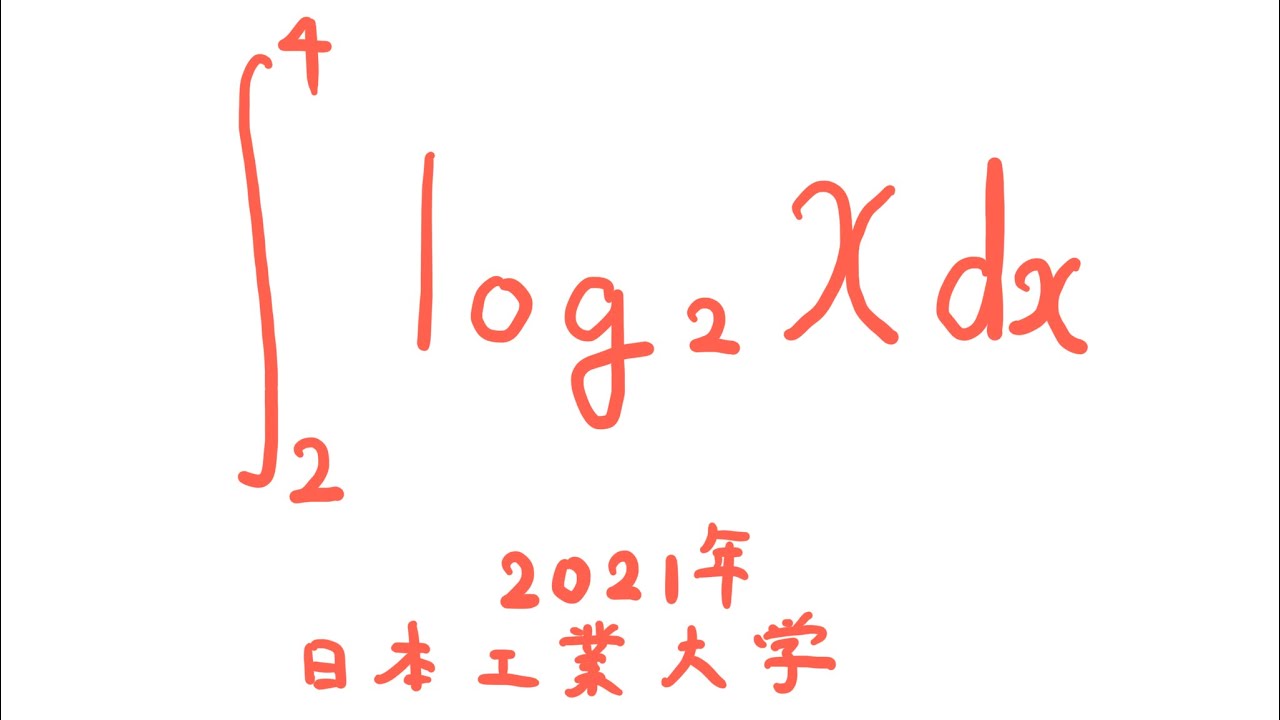
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4} log_2\ x\ dx$
出典:2021年日本工業大学
この動画を見る
$\displaystyle \int_{2}^{4} log_2\ x\ dx$
出典:2021年日本工業大学
福田の数学〜東北大学2024年理系第1問〜放物線と接線と面積

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $a$を正の実数とし、$f(x)$=$x^2$-$2ax$+$4a^2$ とする。Oを原点とする$xy$平面上の放物線C:$y$=$f(x)$の頂点をAとする。直線OAとCの交点のうちAと異なるものをP($p$,$f(p)$)とし、OからCへ引いた接線の接点をQ($q$,$f(q)$)とする。ただし、$q$>0 とする。
(1)$p$,$q$の値を$a$を用いて表せ。また、$p$>$q$であることを示せ。
(2)放物線Cの$q$≦$x$≦$p$の部分、線分OP、および線分OQで囲まれた図形の面積をSとおく。Sを$a$を用いて表せ。
(3)(2)のSに対し、S=$\frac{2}{3}$ となるときの$a$の値を求めよ。
この動画を見る
$\Large{\boxed{1}}$ $a$を正の実数とし、$f(x)$=$x^2$-$2ax$+$4a^2$ とする。Oを原点とする$xy$平面上の放物線C:$y$=$f(x)$の頂点をAとする。直線OAとCの交点のうちAと異なるものをP($p$,$f(p)$)とし、OからCへ引いた接線の接点をQ($q$,$f(q)$)とする。ただし、$q$>0 とする。
(1)$p$,$q$の値を$a$を用いて表せ。また、$p$>$q$であることを示せ。
(2)放物線Cの$q$≦$x$≦$p$の部分、線分OP、および線分OQで囲まれた図形の面積をSとおく。Sを$a$を用いて表せ。
(3)(2)のSに対し、S=$\frac{2}{3}$ となるときの$a$の値を求めよ。
「安定の良問」 by にっし~Diaryさん #極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
#61数検1級1次「よくできた問題」

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典:数検1級1次
この動画を見る
$(x-1)^7-(x^7-1)$を実数係数の範囲で因数分解せよ
出典:数検1級1次
#会津大学(2009) #定積分 #Shorts
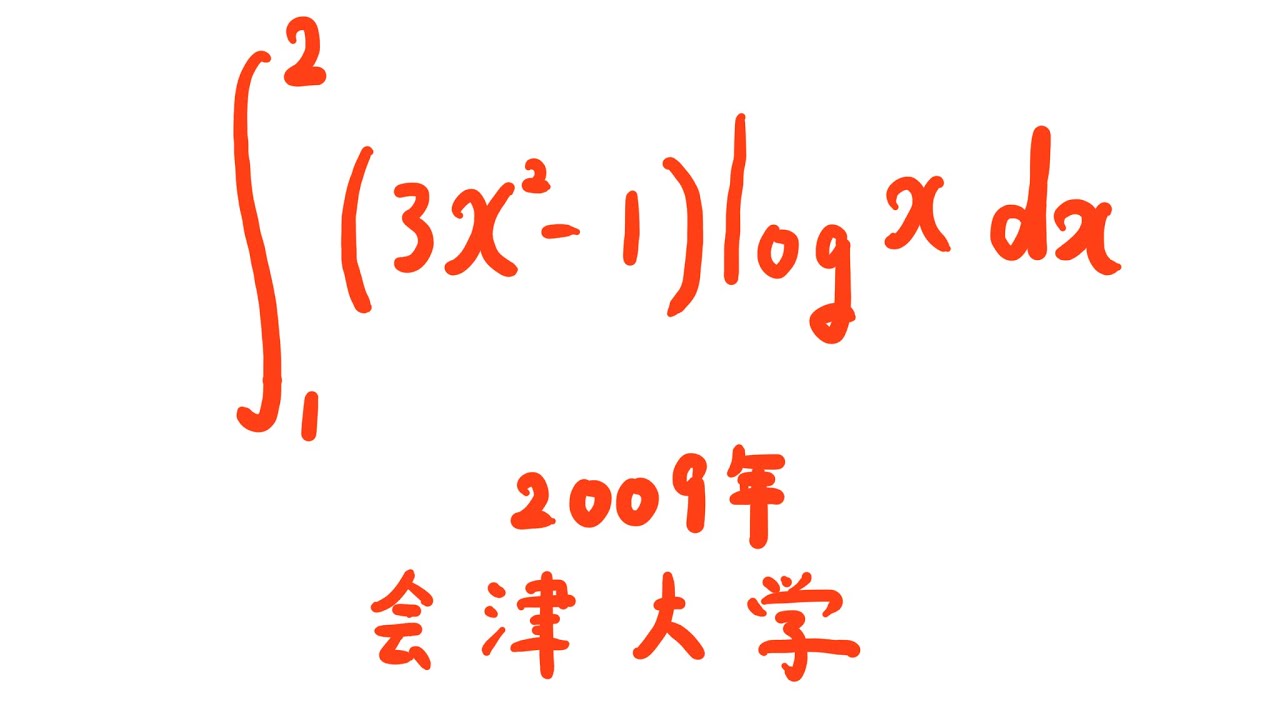
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典:2009年会津大学
この動画を見る
$\displaystyle \int_{1}^{2} (3x^3-1)log\ x\ dx$
出典:2009年会津大学
#59数検1級1次「国立大の入試問題の代表的な題材」

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典:数検1級1次
この動画を見る
$n$を正の整数とするとき定積分
$\displaystyle \int_{0}^{1} (log_e\ x)^n\ dx$の値を$n$に関する式で表せ。
出典:数検1級1次
大学入試問題#783「おもろいタイプ」 岡山県立大学中期(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典:2011年青山県立大学中期 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{x} \displaystyle \frac{1}{\sqrt{ 1-t^2 }}\ dt(0 \leq x \leq 1)$において
$\displaystyle \int_{0}^{\frac{1}{2}} f(x)\ dx$を求めよ
出典:2011年青山県立大学中期 入試問題
大学入試問題#782「もう何回目だろうか」 横浜市立大学(2004) #区分求積法

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典:2004年横浜市立大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\displaystyle \frac{(2n+1)(2n+2)・・・(2n+n)}{(n+1)(n+2)・・・(n+n)}\}^\frac{1}{n}$
出典:2004年横浜市立大学 入試問題
#宮崎大学(2017) #定積分 #Shorts
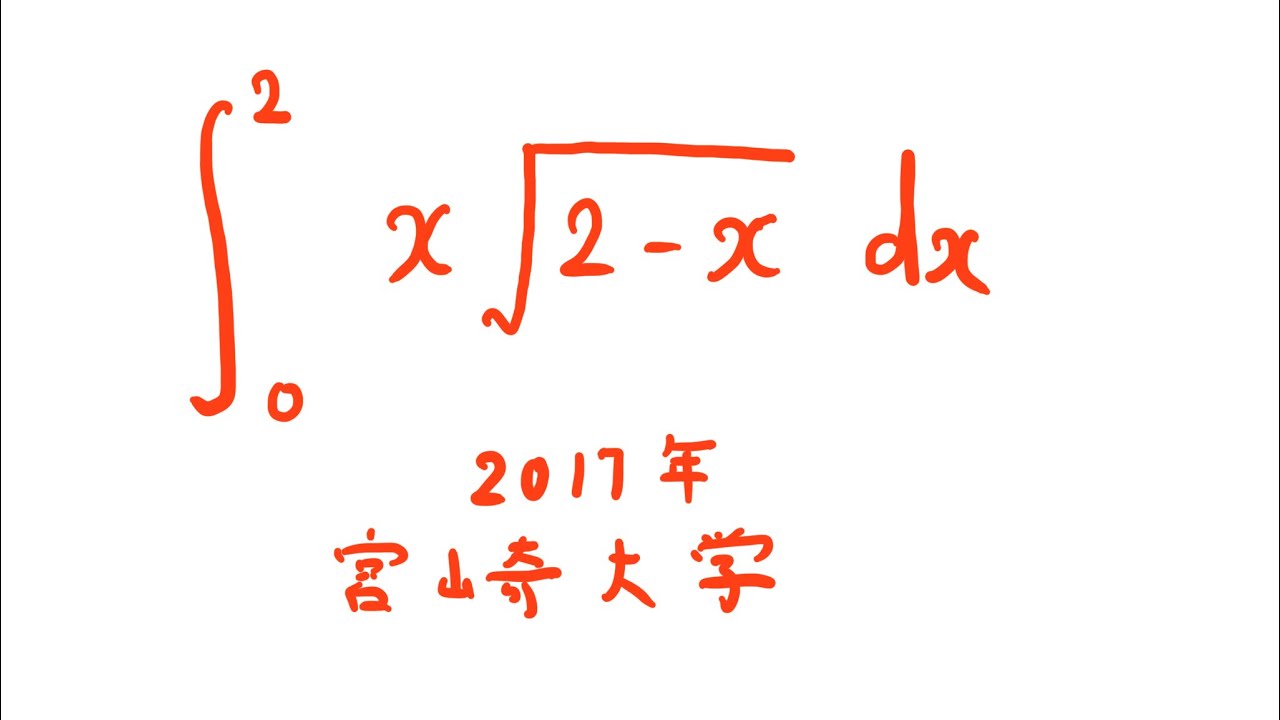
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典:2017年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{2} x\sqrt{ 2-x }\ dx$
出典:2017年宮崎大学
大学入試問題#781「絶対値付きの積分は、なんか苦手!」 久留米大学医学部(2005) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#久留米大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典:2005年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-2\sin\ 2x|\ dx$
出典:2005年久留米大学医学部 入試問題
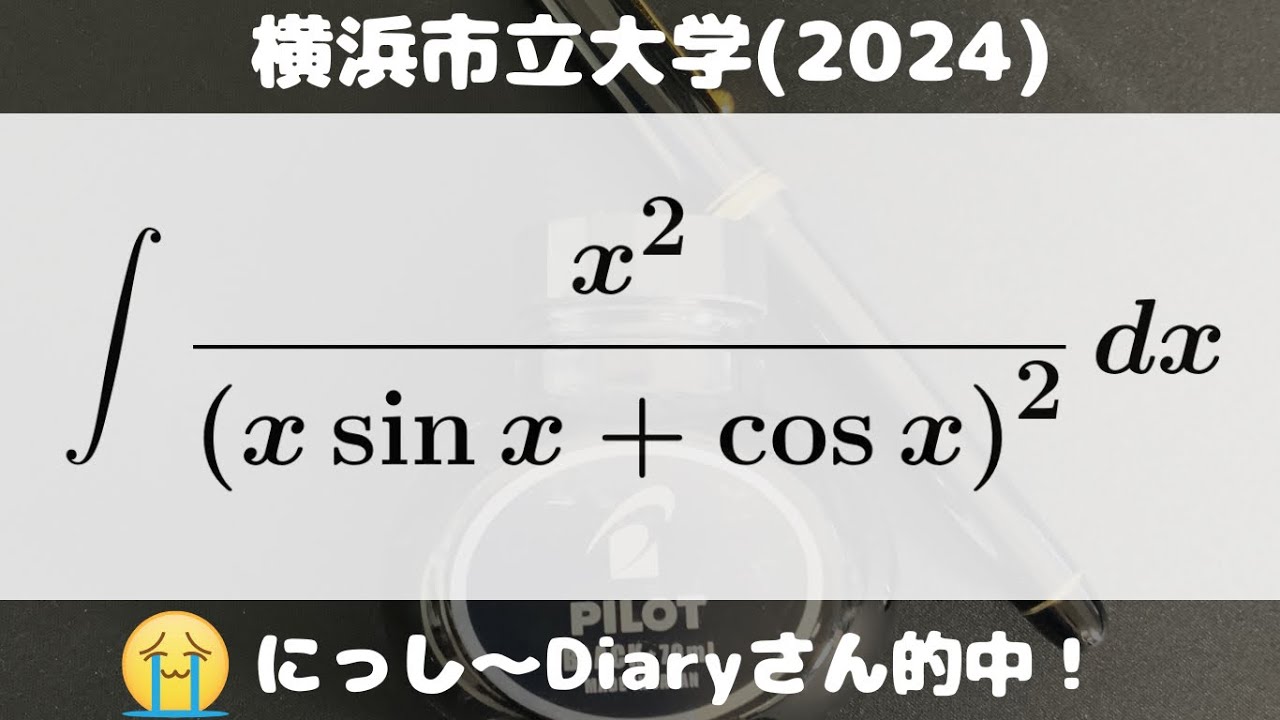
大学入試問題#780「この当て方は、凄すぎ!横浜市立の先生は視聴者かな!?w」 横浜市立大学(2024) #定積分
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典:2024年横浜市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(x\ \sin\ x+\cos\ x)^2} dx$
出典:2024年横浜市立大学
#広島市立大学(2011) #定積分 #Shorts
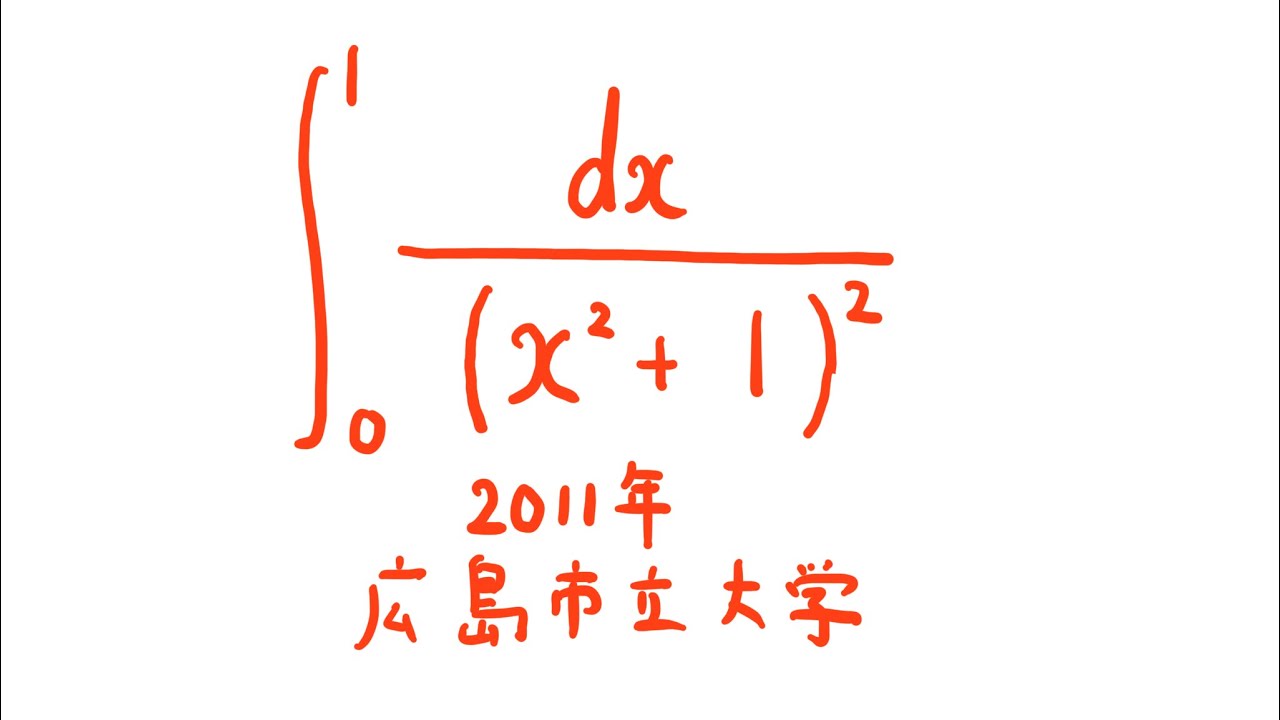
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^2+1)^2}$
出典:2011年広島市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^2+1)^2}$
出典:2011年広島市立大学
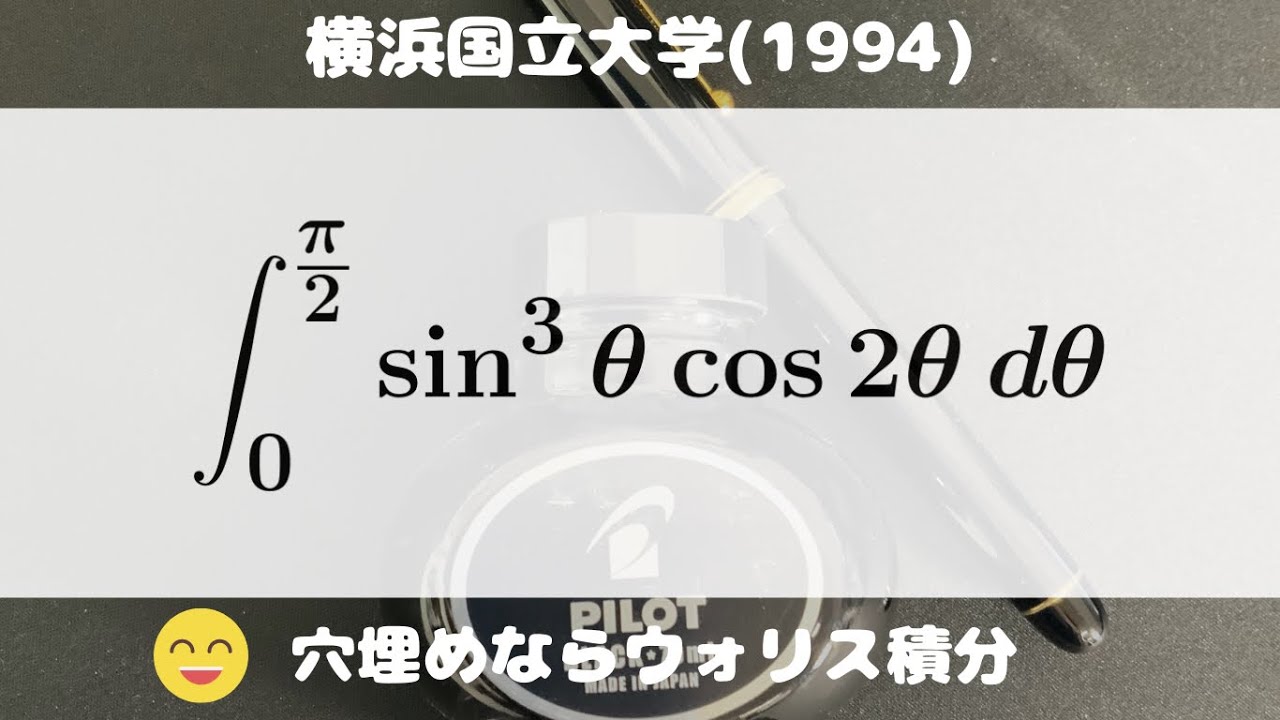
大学入試問題#778「ウォリス積分なら一撃」 横浜国立大学(1994) #定積分
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^3\theta\ \cos2\theta\ d\theta$
出典:1994年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^3\theta\ \cos2\theta\ d\theta$
出典:1994年横浜国立大学 入試問題
【短時間でポイントチェック!!】定積分で表された関数の極値を求める問題〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$f(x)=\displaystyle \int_{2}^{x} t(t-2) dt$の極値を求めよ。
この動画を見る
$f(x)=\displaystyle \int_{2}^{x} t(t-2) dt$の極値を求めよ。
【短時間でポイントチェック!!】定積分で表された関数の極値を求める問題〔現役講師解説、数学〕

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#不定積分・定積分#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$f(x)=\displaystyle \int_{2}^{x} t(t-2)dt$の極値を求めよ。
この動画を見る
$f(x)=\displaystyle \int_{2}^{x} t(t-2)dt$の極値を求めよ。
大学入試問題#776「シグマの気持ち」 横浜国立大学(1996)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典:1996年横浜国立大学
この動画を見る
$\displaystyle \lim_{ n \to +\infty } \displaystyle \frac{1}{n}log\{\displaystyle \frac{n}{n}・\displaystyle \frac{n+2}{n}・\displaystyle \frac{n+4}{n}・・・\displaystyle \frac{n+2(n-1)}{n}\}$
出典:1996年横浜国立大学
#広島市立大学(2016) #定積分 #Shorts
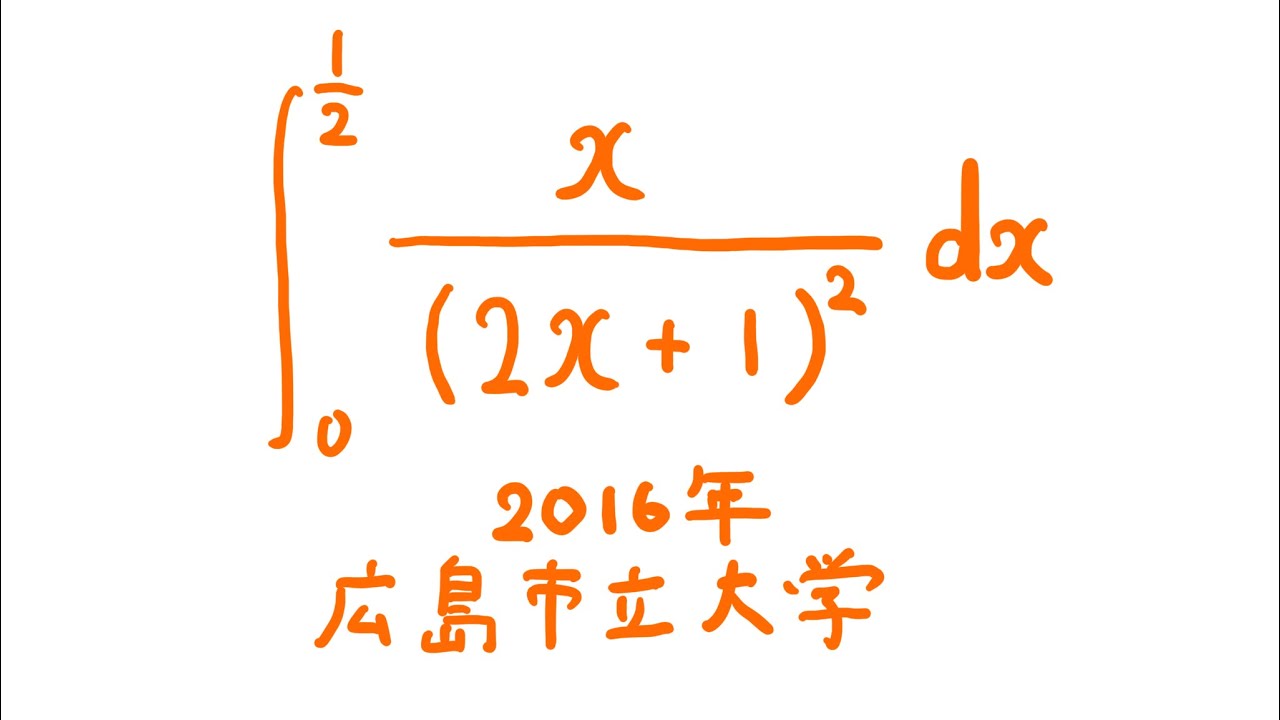
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典:2016年広島市立大学
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} \displaystyle \frac{x}{(2x+1)^2} dx$
出典:2016年広島市立大学
