数Ⅱ
数Ⅱ
福田のおもしろ数学334〜sin3°の値を求める
福田のおもしろ数学332〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
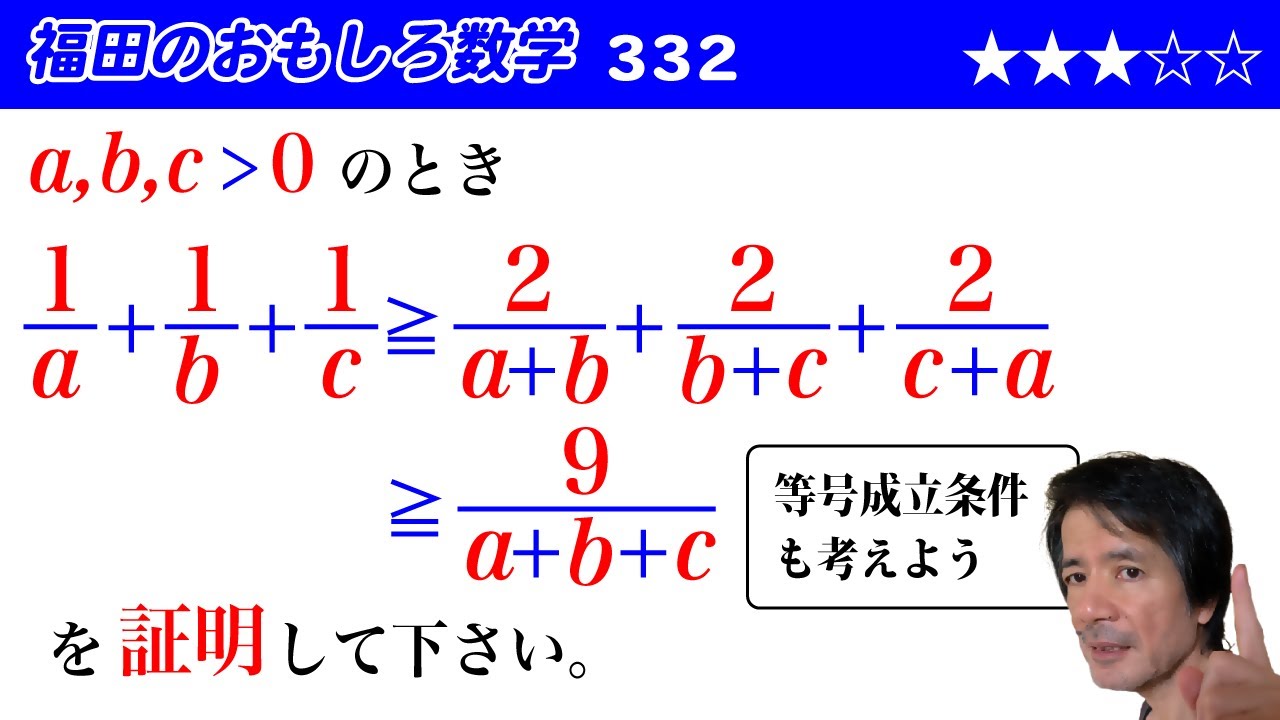
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
この動画を見る
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
福田のおもしろ数学331〜連立の不定方程式の整数解
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
この動画を見る
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
福田のおもしろ数学328〜多項式の性質を繰り返し用いて多項式を求める
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師：
福田次郎
問題文全文(内容文)：
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
この動画を見る
実数係数の多項式$P(x)$が任意の実数$\theta$に対して$P(\cos \theta +\sin \theta)=P(\cos \theta -\sin \theta)$を満たすとき、$P(x)=a_0+a_1 (1-x^2)^2+a_2 (1-x^2)^4 +\cdots+a_n (1-x^2)^{2n}$であることを証明して下さい。($a_0 ,a_1 ,\cdots ,a_n$は実数、$n$は0以上の整数)
福田のおもしろ数学325〜不定方程式の自然数解の個数
単元：
#数Ⅱ#式と証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$$a,b,nは正の整数とする。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{n}$$
$$を満たす(a,b)の組の個数が2017であるとき$$
$$nが平方数であることを示せ。$$
この動画を見る
$$a,b,nは正の整数とする。$$
$$\frac{1}{a}+\frac{1}{b}=\frac{1}{n}$$
$$を満たす(a,b)の組の個数が2017であるとき$$
$$nが平方数であることを示せ。$$
#高専 #極限_75
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{1}{\sqrt{n^2+kn}}$を解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{1}{\sqrt{n^2+kn}}$を解け.
大小比較の難問！どう解く？
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
e^πとπ^eの大小を比較せよ。
この動画を見る
e^πとπ^eの大小を比較せよ。
福田のおもしろ数学319〜桁数と極限
単元：
#数Ⅱ#指数関数と対数関数#対数関数#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
自然数 $n$ に対して $3^n$ の桁数を $k_n$ とするとき、$\displaystyle \lim_{n \to \infty} \frac{k_n}{n}$ を求めよ。
この動画を見る
自然数 $n$ に対して $3^n$ の桁数を $k_n$ とするとき、$\displaystyle \lim_{n \to \infty} \frac{k_n}{n}$ を求めよ。
高校2年生から京大に挑戦！積分習いたての人にも解ける問題【京都大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
2x, 5-x, 2のうち最小の数をf(x)とし、g(x)=xf(x)とおく。y=g(x)とx軸で囲まれた部分の面積は？
この動画を見る
2x, 5-x, 2のうち最小の数をf(x)とし、g(x)=xf(x)とおく。y=g(x)とx軸で囲まれた部分の面積は？
福田のおもしろ数学314〜条件付き循環形式の不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師：
福田次郎
問題文全文(内容文)：
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。
この動画を見る
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。
福田の数学〜北里大学2024医学部第1問(1)〜三角関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
この動画を見る
2つの実数x,yは$x^2+y^2 \leqq 4,x \geqq 0 $を満たすとする。このとき、$3x+4y-3$の最小値は$\boxed{ ア }$、最大値は$\boxed{ イ }$である。また、$3x^2+4xy-3y^2$の最大値は$\boxed{ ウ }$である。
難易度鬼高の定積分！ By BBBさん
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\sqrt2}^{2} \dfrac{x}{(1+x)\sqrt{x^2-1}}dx$を解け.
この動画を見る
$\displaystyle \int_{\sqrt2}^{2} \dfrac{x}{(1+x)\sqrt{x^2-1}}dx$を解け.
福田の数学〜早稲田大学2024社会科学部第1問〜領域における最大最小
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
この動画を見る
$$連立不等式
y≦-\frac{2}{3}x+4, y≧x-1,x≧0,y≧0
の表す領域をDとする。点(x,y)が領域Dを動くとき、次の問いに答えよ。
$$(1)領域Dを座標平面上に図示せよ。$$
$$(2)-2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(3)2x+yの最大値と、そのときのx,yの値を求めよ。$$
$$(4)aがすべての実数を動くとき、ax+yの最大値をaで分類せよ。$$
#電気通信大学2024#極限_72
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
福田の数学〜早稲田大学2024商学部第2問〜正24角形の頂点を結んでできる四角形の面積と確率
単元：
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面において、単位円上の24個の点を${\textrm P}_n(\cos\dfrac{n}{12}\pi,\sin\dfrac{n}{12}\pi)~(n=1,2,3,\cdots,24)$とする。1から24までの番号を付けた24枚のカードから4枚取り出す。取り出したカードの番号を$a,b,c,d$とするとき、点${\textrm P}_a,{\textrm P}_b,{\textrm P}_c,{\textrm P}_d$を頂点とする四角形を$R$とする。四角形$R$の面積の取りうる値を大きい順に$S_1,S_2,S_3$とする。
(1)$S_2$を求めよ。
(2)四角形$R$の面積が$S_3$になる確率を求めよ。
この動画を見る
座標平面において、単位円上の24個の点を${\textrm P}_n(\cos\dfrac{n}{12}\pi,\sin\dfrac{n}{12}\pi)~(n=1,2,3,\cdots,24)$とする。1から24までの番号を付けた24枚のカードから4枚取り出す。取り出したカードの番号を$a,b,c,d$とするとき、点${\textrm P}_a,{\textrm P}_b,{\textrm P}_c,{\textrm P}_d$を頂点とする四角形を$R$とする。四角形$R$の面積の取りうる値を大きい順に$S_1,S_2,S_3$とする。
(1)$S_2$を求めよ。
(2)四角形$R$の面積が$S_3$になる確率を求めよ。
東京大学の整数問題！5つの文字を求める！？どう解く？
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算（整式・展開・因数分解）#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
福田のおもしろ数学307〜不等式の証明エレガントに証明しよう
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a\geqq 1,b\geqq 1$のとき、$\sqrt{a-1}+\sqrt{b-1}\leqq \sqrt{ab}$であることを示して下さい。
この動画を見る
$a\geqq 1,b\geqq 1$のとき、$\sqrt{a-1}+\sqrt{b-1}\leqq \sqrt{ab}$であることを示して下さい。
福田のおもしろ数学306〜5次方程式の5つの解がすべて実数にはなれない条件
単元：
#数Ⅱ#式と証明#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
この動画を見る
実数係数の5次方程式
$z^5+az^4+bz^3+cz^2+dz+e=0$
について$2a^2\lt 5b$のときはすべての解が実数にはなれないことを示してください。
#高専 #定積分_71
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{0} \dfrac{dx}{\sqrt{x^2+2x+2}}$を解け.
高専定期試験
この動画を見る
$\displaystyle \int_{-1}^{0} \dfrac{dx}{\sqrt{x^2+2x+2}}$を解け.
高専定期試験
福田のおもしろ数学303〜階乗のたくさんある分数の和
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
この動画を見る
$\displaystyle \frac{1}{2! 17!} $$\displaystyle + \frac{1}{3! 16!} $$\displaystyle + \frac{1}{4! 15!}$$+ \cdots $$\displaystyle + \frac{1}{9! 10!} $$\displaystyle = \frac{N}{1! 18!}$ を満たす $N$ を求めよ。
福田のおもしろ数学301〜4次方程式の解と係数の関係
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
この動画を見る
$x ^ 4 - 18x ^ 3 + k x ^ 2 + 200x - 1984 = 0 $の2つの解の積が$-32$のとき、実数$k$の値は?
福田の数学〜早稲田大学2024教育学部第1問(4)〜領域と奇跡
単元：
#数Ⅰ#数Ⅱ#２次関数#図形と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{$1$} \ (4) \\
\end{eqnarray}
$
$xy$平面上に3点$O(0,0),A(1,0),B(1,1)$をとる。点$(x,y)$が三角形$OAB$の周および内部を動くときに点$(x+y,xy)$が動く範囲の面積を求めよ。
福田のおもしろ数学299〜三角関数で表された式の値
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
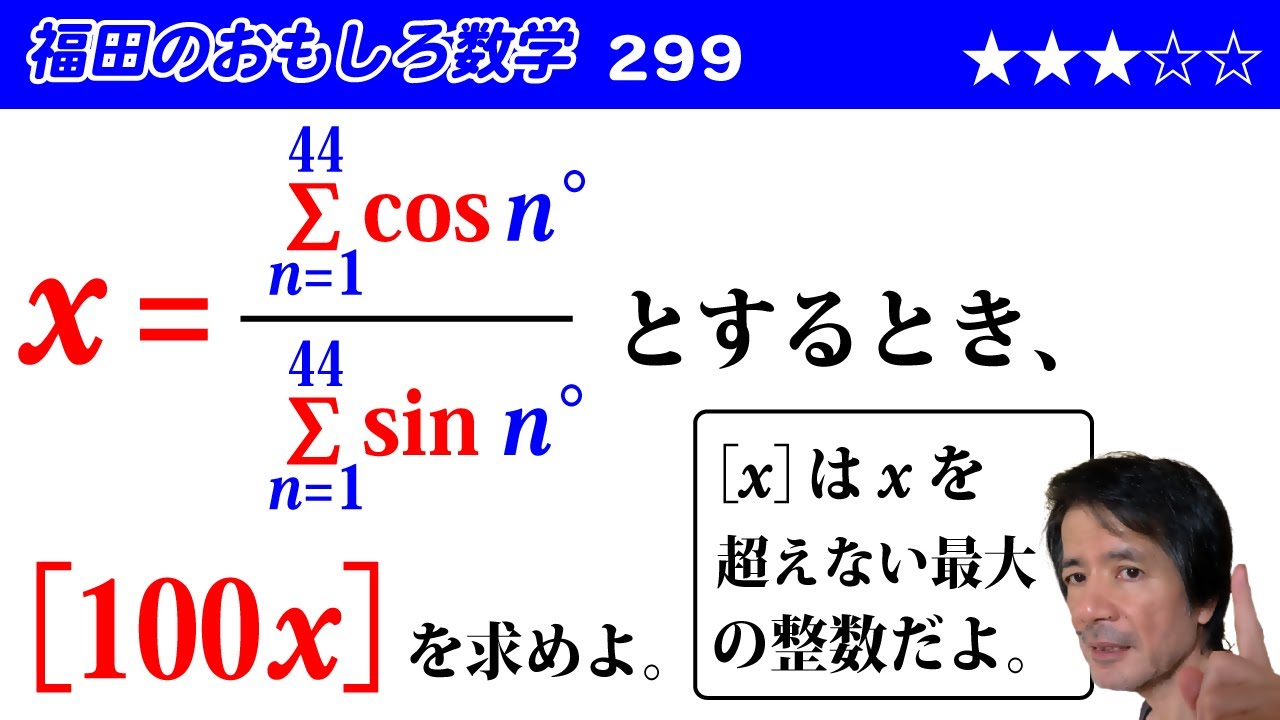
$x = \frac{\displaystyle \sum_{i=1}^{44} cos \ n^{ \circ }}{\displaystyle \sum_{i=1}^{44} sin \ n^{ \circ }}$とするとき、$[100x]$を求めよ。
この動画を見る
$x = \frac{\displaystyle \sum_{i=1}^{44} cos \ n^{ \circ }}{\displaystyle \sum_{i=1}^{44} sin \ n^{ \circ }}$とするとき、$[100x]$を求めよ。
この式はあれしかない！！どう解く？
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
この動画を見る
多項式(x^100+1)^100+(x^2+1)^100+1は多項式x^2+x+1で割り切れるか。
#関西大学2024 #方程式_70
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
この動画を見る
$x^2+x-\dfrac{2}{x}+\dfrac{4}{x^2}-6=0$
の解のうち最小のものを求めよ.
2024関西大学過去問題
福田の数学〜慶應義塾大学2024環境情報学部第4問〜球の一部の体積と距離の最大
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
（１）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
（２）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
（３）$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。（ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。）
この動画を見る
（１）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq |x|$ が定める立体の体積は$\frac{\fbox{アイ}}{\fbox{ウエ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\fbox{オカ}$である。
（２）$xyz$空間において、不等式 $x^2+y^2+z^2\leqq|x|+|y|$ が定める立体の体積は$\frac{\fbox{キク}}{\fbox{ケコ}}\pi$である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は$\sqrt{\fbox{サシ}}$ である。
（３）$xyz$ 空間において、不等式 $x^2+y^2+z^2\leqq$$ |x| + |y| + |z| - \frac{1}{4}$ が定める立体の体積は$(\fbox{スセ}$$+\frac{\fbox{ソタ}}{\fbox{チツ}}\sqrt{\fbox{テト}})\pi$ である。また、原点を中心とする球面がこの立体と共有点をもつとき、球面の半径の最大値は $\frac{\fbox{ナニ}}{\fbox{ヌネ}}\sqrt{\fbox{ノハ}}$ $+\frac{\fbox{ヒフ}}{\fbox{ヘホ}}\sqrt{\fbox{マミ}}$ である。（ただし、$\fbox{ノハ} \le \fbox{マミ}$ とする。）
福田のおもしろ数学294〜対数方程式の解の積
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{2024}x^{\log_{2024}x}\ =\ x^2$を満たす実数$x$の積の下3桁を求めよ。
この動画を見る
$\sqrt{2024}x^{\log_{2024}x}\ =\ x^2$を満たす実数$x$の積の下3桁を求めよ。
福田のおもしろ数学293〜三角方程式を満たす正の整数xの最小値
単元：
#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数とグラフ#加法定理とその応用
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
この動画を見る
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
福田の数学〜慶應義塾大学2024環境情報学部第1問(2)〜対数不等式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
実数x, y, zが \\
\left\{
\begin{array}{1}
x > 1, \ y > 1 , \ z > 1\\
log_{x}y + log_{y}x + log_{y}z \leqq 6\\
4xz + 3x - 7y - 5z = -5
\end{array}
\right.
\\を満たしているとき \
x = \frac{\fbox{アイ}}{\fbox{ウエ}}, \
y = \frac{\fbox{オカ}}{\fbox{キク}}, \
z = \frac{\fbox{ケコ}}{\fbox{サシ}},
\end{eqnarray}
$
#関西学院大学2006#不定積分_68
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問