 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
【数Ⅱ】【三角関数】加法定理の応用7 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
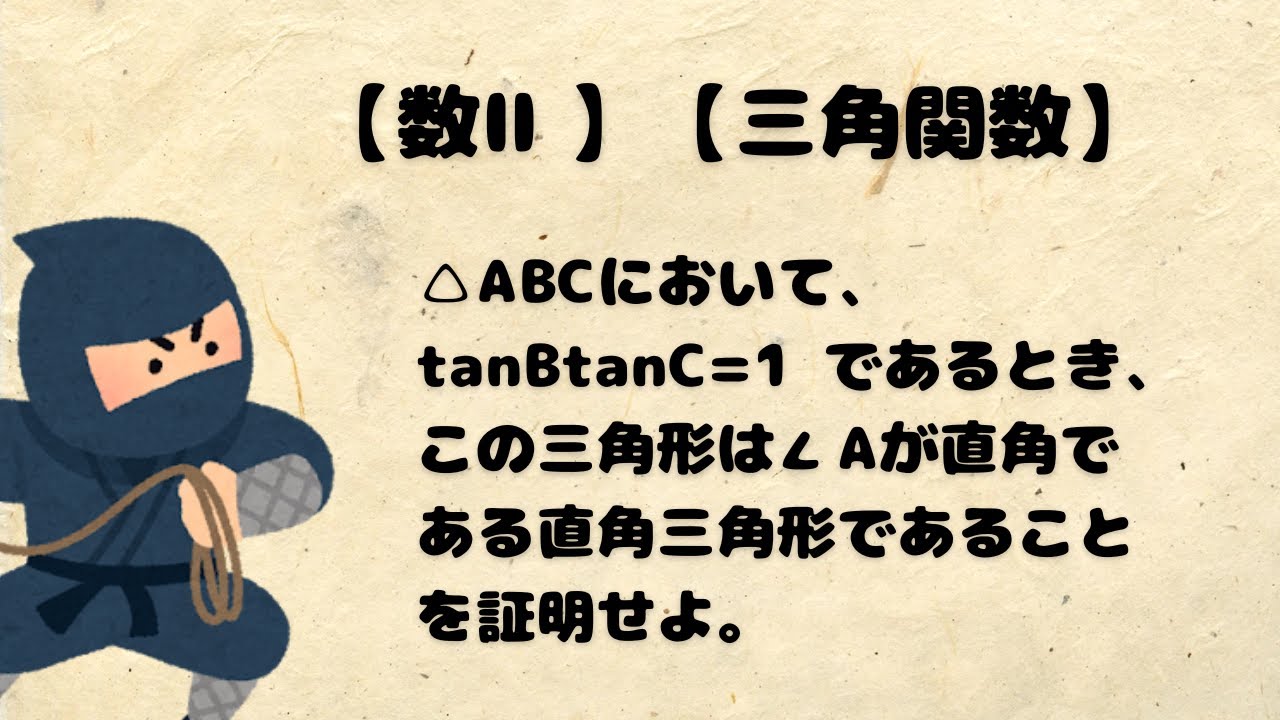
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
この動画を見る
△ABCにおいて、 tanBtanC=1 であるとき、この三角形は∠Aが直角である直角三角形であることを証明せよ。
【数Ⅱ】【三角関数】加法定理の応用6 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
この動画を見る
次の関数のグラフをかけ。また、その周期をいえ。
(1) y=cos² x
(2) y=3sin² x+cos² x
【数Ⅱ】【三角関数】加法定理の応用5 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
この動画を見る
-π/2≦x≦π/2 とする。関数 y=2sinx-cos2x の最大値、最小値と、そのときのxの値を求めよ。
【数Ⅱ】【三角関数】加法定理の応用4 ※問題文は概要欄
単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
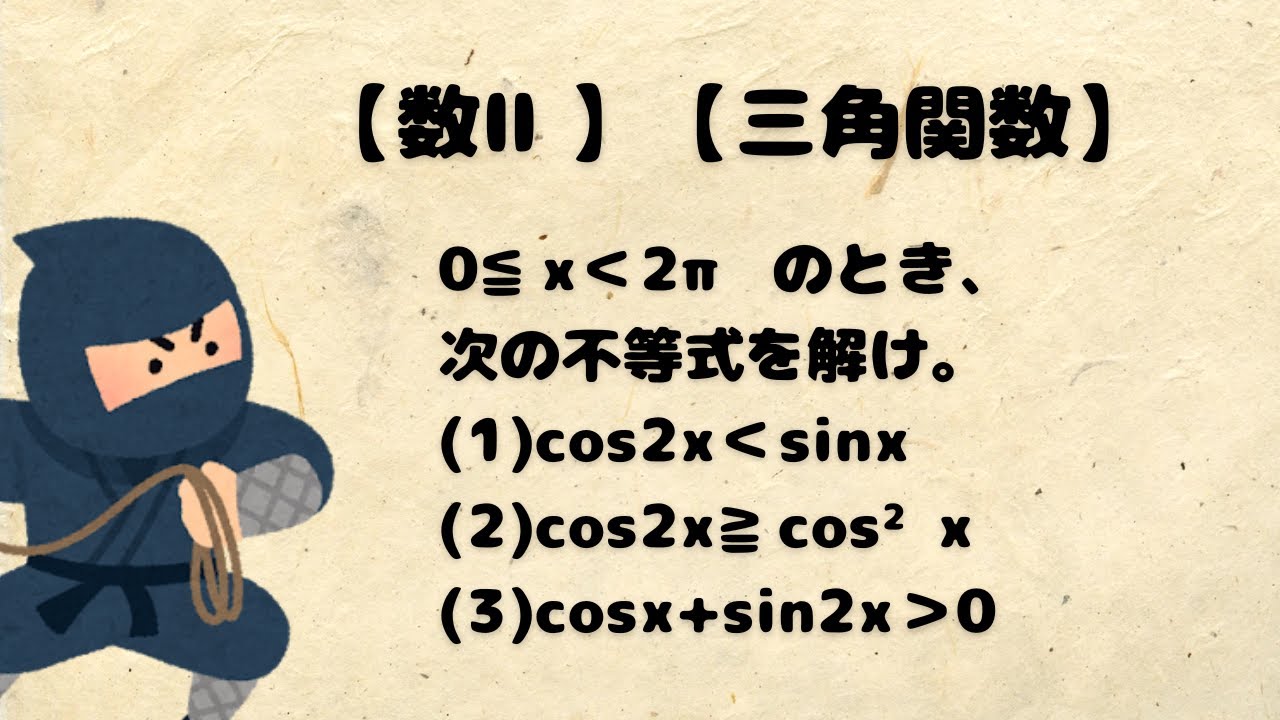
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
この動画を見る
0≦x<2π のとき、次の不等式を解け。
(1)cos2x<sinx
(2)cos2x≧cos² x
(3)cosx+sin2x>0
【数Ⅱ】【三角関数】加法定理の応用3 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
この動画を見る
0≦x<2π のとき、次の方程式を解け。
(1)cos2x=cosx
(2)sin2x=cosx
(3)2cos2x+4cosx-1=0
(4)sinx(1+cos2x)+sin2x(1+cosx)=0
【数Ⅱ】【三角関数】加法定理の応用2 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
この動画を見る
tanα=t のときcos² α ,sin2α ,cos2α を t で表せ。
【数Ⅱ】【三角関数】加法定理の応用1 ※問題文は概要欄

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#三角関数#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
この動画を見る
等式cos3α+sin3α=(cosα-sinα)(1+2sin2α)を証明せよ。
【数Ⅱ】【微分法と積分法】接線からの関数決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
この動画を見る
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
【数Ⅱ】【微分法と積分法】係数比較から関数の決定 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
この動画を見る
2次関数$f(x)$の1つの不定積分$F(x)$が$xf(x)-2x^3+3x^2$に等しく、$f(1)=0$であるとき、$f(x)$を求めよ。
福田のおもしろ数学432〜ガウス記号を含んだ式が成り立たない条件

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
この動画を見る
$n+\left[\dfrac{n}{2}\right] \neq \left[\dfrac{n}{6}\right]+\left[\dfrac{2n}{3}\right]$
を満たす自然数$n$をすべて求めよ。
福田のおもしろ数学431〜sin^318°+sin^218°の値を求める

福田の数学〜京都大学2025理系第1問(2−1)〜定積分の計算
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
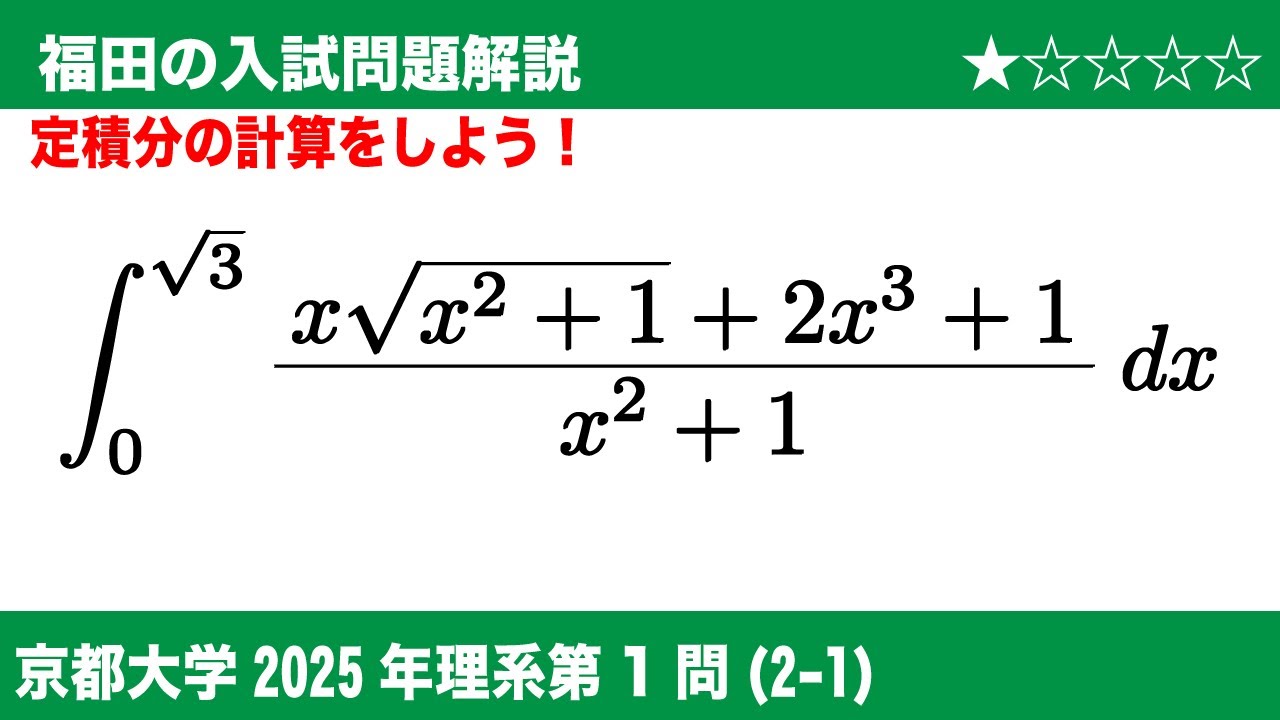
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
福田の数学〜京都大学2025理系第1問(1)〜複素数の絶対値の取り得る値の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
【数Ⅱ】【図形と方程式】2直線の関係4 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような三角形の面積を求めよ。
(1)3点(-1,1),(3,2),(1,4)を頂点とする三角形
(2)3直線$x-3y=-5,4x+3y=-5,2x-y=5$で作られる三角形
平面上の2点をA(1,1),B(2,3)とする。
点Pが放物線$y=x^{2}+4x+11$を動くとき、$\triangle$PABの面積の最小値を求めよ。
この動画を見る
次のような三角形の面積を求めよ。
(1)3点(-1,1),(3,2),(1,4)を頂点とする三角形
(2)3直線$x-3y=-5,4x+3y=-5,2x-y=5$で作られる三角形
平面上の2点をA(1,1),B(2,3)とする。
点Pが放物線$y=x^{2}+4x+11$を動くとき、$\triangle$PABの面積の最小値を求めよ。
【数Ⅱ】【図形と方程式】2直線の関係3 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1
直線$y=2x$を$l$とするとき、次のものを求めよ。
(1)$l$に関して、点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して、直線$3x+y=15$と対称な直線の方程式
問2
$k$を定数とする。直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る。その定点の座標を求めよ。
問3
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ、3点$(1,ー1),(2,ー3),(a,b)$は一直線上にあることを証明せよ。
この動画を見る
問1
直線$y=2x$を$l$とするとき、次のものを求めよ。
(1)$l$に関して、点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して、直線$3x+y=15$と対称な直線の方程式
問2
$k$を定数とする。直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る。その定点の座標を求めよ。
問3
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ、3点$(1,ー1),(2,ー3),(a,b)$は一直線上にあることを証明せよ。
【数Ⅱ】【図形と方程式】2直線の関係2 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように、定数$k$の値を求めよ。
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ。
2直線$x-y+1=0,3x+2y-12=0$の交点を通り、次の条件を満たす直線の方程式を、それぞれ求めよ。
(1)直線$5xー6yー8=0$に平行である。
(2)直線$5xー6yー8=0$に垂直である。
この動画を見る
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように、定数$k$の値を求めよ。
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ。
2直線$x-y+1=0,3x+2y-12=0$の交点を通り、次の条件を満たす直線の方程式を、それぞれ求めよ。
(1)直線$5xー6yー8=0$に平行である。
(2)直線$5xー6yー8=0$に垂直である。
【数Ⅱ】【図形と方程式】2直線の関係1 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
この動画を見る
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
【数Ⅱ】【図形と方程式】内分外分の利用 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
この動画を見る
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
【数Ⅱ】【図形と方程式】内分と外分の基本、点と直線 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
この動画を見る
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
【数Ⅱ】【図形と方程式】内分外分重心 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2+AC^2=BG^2+CG^2+4AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
この動画を見る
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2+AC^2=BG^2+CG^2+4AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
福田の数学〜東京大学2025文系第4問〜放物線で囲まれた面積の最大値

単元:
#連立方程式#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
この動画を見る
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
福田のおもしろ数学427〜累乗の繰り返しの数と2025の大小比較

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a=\sqrt[2025]{2025}$とする。
$a^{a^{a^{\cdots a}}} \}2025$個と$2025$の大小を比較して下さい。
この動画を見る
$a=\sqrt[2025]{2025}$とする。
$a^{a^{a^{\cdots a}}} \}2025$個と$2025$の大小を比較して下さい。
福田の数学〜東京大学2025文系第2問〜三角形の3頂点を中心とする3つの円で3辺を含む条件と三角形を含む条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
この動画を見る
$\boxed{2}$
平面上で$AB=AC=1$である
二等辺三角形$ABC$を考える。
正の実数$r$に対し、$A,B,C$それぞれを中心とする
半径$r$の円$3$つを合わせた領域を$D_r$とする。
ただし、この問いでは、
三角形と円は周とその内部からなるものとする。
辺$AB,AC,BC$がすべて$D_r$に
含まれるような最小の$r$を$s$、
三角形$ABC$が
$D_r$に含まれるような最小の$r$を$t$と表す。
(1)$\angle BAC=\dfrac{\pi}{3}$のとき、$s$と$t$を求めよ。
(2)$\angle BAC=\dfrac{2\pi}{3}$のとき、$s$と$t$を求めよ。
(3)$0\lt \theta \lt \pi$を満たす$\theta$に対して、
$\angle BAC=\theta$のとき、$s$と$t$を$\theta$を用いて表せ。
$2025$年東京大学文系過去問題
【数Ⅱ】【式と証明】不等式の証明8 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)a>0のとき、a+16/a の最小値を求めよ。
(2)a>0のとき、(a+1/a)(a+16/a) の最小値を求めよ。
(3)a>0 ,b>0 ,ab=12のとき、a+b の最小値を
求めよ。
(4)a>0 ,b>0 ,$2a+3b=4\sqrt{2}$ のとき、abの最大値を求めよ。
この動画を見る
(1)a>0のとき、a+16/a の最小値を求めよ。
(2)a>0のとき、(a+1/a)(a+16/a) の最小値を求めよ。
(3)a>0 ,b>0 ,ab=12のとき、a+b の最小値を
求めよ。
(4)a>0 ,b>0 ,$2a+3b=4\sqrt{2}$ のとき、abの最大値を求めよ。
【数Ⅱ】【式と証明】不等式の証明7 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>0,b>0,c>0のとき、(a+b)(b+c)(c+a)≧8abc が成り立つことを証明せよ。また、等号が成り立つのはどのようなときか。
この動画を見る
a>0,b>0,c>0のとき、(a+b)(b+c)(c+a)≧8abc が成り立つことを証明せよ。また、等号が成り立つのはどのようなときか。
【数Ⅱ】【式と証明】不等式の証明6 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$0<a<b$ ,$a+b=2$のとき、$1$ ,$ab$ ,$a^2+b^2$ を小さい方から順に並べよ。
この動画を見る
$0<a<b$ ,$a+b=2$のとき、$1$ ,$ab$ ,$a^2+b^2$ を小さい方から順に並べよ。
【数Ⅱ】【式と証明】不等式の証明5 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>0 ,b>0のとき、$\sqrt{ab}$ , $\displaystyle \frac{2ab}{a+b}$ の大小関係を調べよ。
この動画を見る
a>0 ,b>0のとき、$\sqrt{ab}$ , $\displaystyle \frac{2ab}{a+b}$ の大小関係を調べよ。
【数Ⅱ】【式と証明】不等式の証明4 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
不等式$\sqrt{a^2+b^2}≦|a|+|b|≦\sqrt{2}\sqrt{a^2+b^2}$ を証明せよ。
この動画を見る
不等式$\sqrt{a^2+b^2}≦|a|+|b|≦\sqrt{2}\sqrt{a^2+b^2}$ を証明せよ。
【数Ⅱ】【式と証明】不等式の証明3 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a>b≧c>0 のとき、次の空欄に記号≧ ,≦ ,> ,<のどれかを記入して正しい関係が成り立つようにせよ。ただし、これが不可能の場合には×とせよ。
(1)$2(ac+b^2 ) □ b(4a+c)$
(2)$a^2+2bc□2ab+ca$
(3)$a^2+2(b^2+c^2) □2a(b+c)$
この動画を見る
a>b≧c>0 のとき、次の空欄に記号≧ ,≦ ,> ,<のどれかを記入して正しい関係が成り立つようにせよ。ただし、これが不可能の場合には×とせよ。
(1)$2(ac+b^2 ) □ b(4a+c)$
(2)$a^2+2bc□2ab+ca$
(3)$a^2+2(b^2+c^2) □2a(b+c)$
【数Ⅱ】【式と証明】不等式の証明2 ※問題文は概要欄

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#式と証明#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を証明せよ。また、等号が成り立つのはどのようなときか。
(1)$x^2+y^2≧6(x-y-3)$
(2)$a^2-ab+b^2≧a+b-1$
(3)$x^2+xy+y^2+3z(x+y+z)≧0$
(4)$\displaystyle \frac{(a^2+b^2+c^2)}{3}≧\displaystyle \frac{(a+b+c)^2}{3}$
この動画を見る
次の不等式を証明せよ。また、等号が成り立つのはどのようなときか。
(1)$x^2+y^2≧6(x-y-3)$
(2)$a^2-ab+b^2≧a+b-1$
(3)$x^2+xy+y^2+3z(x+y+z)≧0$
(4)$\displaystyle \frac{(a^2+b^2+c^2)}{3}≧\displaystyle \frac{(a+b+c)^2}{3}$
