数列とその和（等差・等比・階差・Σ）
数列とその和（等差・等比・階差・Σ）
【数B】数列を30分で総まとめしてみた【1.5倍速再生推奨・教科書レベル】
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
【数B】数列を30分で総まとめ動画です
この動画を見る
【数B】数列を30分で総まとめ動画です
大阪大 等比数列 訂正
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
訂正
自然数の列
$a_{1},a_{2},a_{3},a_{4},a_{5}$は等比数列
$S=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$
$S'=a_{1}-a_{2}-a_{3}-a_{4}-a_{5}$
$T=a^2_{1}+a^2_{2}+a^2_{3}+a^2_{4}+a^2_{5}$
（1）
$\displaystyle \frac{T}{S}=S'$を示せ
（2）
$T$が素数のとき、$T$の値は？
出典：大阪大学 過去問
この動画を見る
訂正
自然数の列
$a_{1},a_{2},a_{3},a_{4},a_{5}$は等比数列
$S=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$
$S'=a_{1}-a_{2}-a_{3}-a_{4}-a_{5}$
$T=a^2_{1}+a^2_{2}+a^2_{3}+a^2_{4}+a^2_{5}$
（1）
$\displaystyle \frac{T}{S}=S'$を示せ
（2）
$T$が素数のとき、$T$の値は？
出典：大阪大学 過去問
等比数列 大阪大
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数の列
$a_{1},a_{2},a_{3},a_{4},a_{5}$は等比数列
$S=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$
$S'=a_{1}-a_{2}-a_{3}-a_{4}-a_{5}$
$T=a^2_{1}+a^2_{2}+a^2_{3}+a^2_{4}+a^2_{5}$
（1）
$\displaystyle \frac{T}{S}=S'$を示せ
（2）
$T$が素数のとき、$T$の値は？
出典：1987年大阪大学 過去問
この動画を見る
自然数の列
$a_{1},a_{2},a_{3},a_{4},a_{5}$は等比数列
$S=a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$
$S'=a_{1}-a_{2}-a_{3}-a_{4}-a_{5}$
$T=a^2_{1}+a^2_{2}+a^2_{3}+a^2_{4}+a^2_{5}$
（1）
$\displaystyle \frac{T}{S}=S'$を示せ
（2）
$T$が素数のとき、$T$の値は？
出典：1987年大阪大学 過去問
岡山県立大 バーゼル問題
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
証明せよ
$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k^2} \leqq 2-\displaystyle \frac{1}{n}$
出典：岡山県立大学 過去問
この動画を見る
証明せよ
$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k^2} \leqq 2-\displaystyle \frac{1}{n}$
出典：岡山県立大学 過去問
開成中学 整数 等差数列の和
単元：
#算数(中学受験)#数列#数列とその和（等差・等比・階差・Σ）#過去問解説(学校別)#数学(高校生)#数B#開成中学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
平方数を3つ以上の連続数の和で表す
（例）$6^2=1+2+3+…+8=11+12+13$
（1）
$7^2$
（2）
$10^2$
（3）
$30^2$は何通りあるか
出典：2018年開成中学校 過去問
この動画を見る
平方数を3つ以上の連続数の和で表す
（例）$6^2=1+2+3+…+8=11+12+13$
（1）
$7^2$
（2）
$10^2$
（3）
$30^2$は何通りあるか
出典：2018年開成中学校 過去問
山形大 三項間漸化式 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_{1}=-1$
一般項を求めよ
$2\displaystyle \sum_{k=1}^n a_{k}=3a_{n+1}-2a_{n}-1$
出典：2006年山形大学 過去問
この動画を見る
$a_{1}=-1$
一般項を求めよ
$2\displaystyle \sum_{k=1}^n a_{k}=3a_{n+1}-2a_{n}-1$
出典：2006年山形大学 過去問
和歌山県立医大 奈良女子大 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B#和歌山県立医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
①$n^3(n^2-1)$が8の倍数であることを示せ($n$)整数
②$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k(k+1)(k+2)(k+3)}$
出典：和歌山県立医科大学/奈良女子大学 過去問
この動画を見る
①$n^3(n^2-1)$が8の倍数であることを示せ($n$)整数
②$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k(k+1)(k+2)(k+3)}$
出典：和歌山県立医科大学/奈良女子大学 過去問
群馬大 整数問題 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$p$素数、$m,n$整数$(m \neq 0)$
$n,p-m,m+n$がこの順に等差数列
$p-m,n,p+m$がこの順に等比数列
$p,m,n$を求めよ
出典：群馬大学 過去問
この動画を見る
$p$素数、$m,n$整数$(m \neq 0)$
$n,p-m,m+n$がこの順に等差数列
$p-m,n,p+m$がこの順に等比数列
$p,m,n$を求めよ
出典：群馬大学 過去問
近畿大 展開 係数 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x+1)(x+3)(x+5)$
$x(x+7)(x+9)(x+11)$
（1）
$x^7$の係数
（2）
$x^6$の係数
出典：2012年近畿大学 過去問
この動画を見る
$(x+1)(x+3)(x+5)$
$x(x+7)(x+9)(x+11)$
（1）
$x^7$の係数
（2）
$x^6$の係数
出典：2012年近畿大学 過去問
広島大 数列の和 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\displaystyle \frac{7}{1・2・3}+\displaystyle \frac{11}{2・3・4}+\displaystyle \frac{15}{3・4・5}+…$
分子は等差数列
分母は連続3数の積
出典：1993年広島大学 過去問
この動画を見る
$\displaystyle \frac{7}{1・2・3}+\displaystyle \frac{11}{2・3・4}+\displaystyle \frac{15}{3・4・5}+…$
分子は等差数列
分母は連続3数の積
出典：1993年広島大学 過去問
2016年度 本試験 数学B 群数列の解き方復習！
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
2016年度 本試験 数学B 群数列の解き方復習解説動画です
この動画を見る
2016年度 本試験 数学B 群数列の解き方復習解説動画です
鹿児島大（医他）数列の和 高校数学 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sum_{k=1}^{n} \displaystyle \frac{2k-1}{2^k}$
出典：鹿児島大学 過去問
この動画を見る
$\sum_{k=1}^{n} \displaystyle \frac{2k-1}{2^k}$
出典：鹿児島大学 過去問
同志社 数列の和 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典：同志社大学 過去問
この動画を見る
$n=1,2,3…$
$a_{n}=\displaystyle \frac{4N+3}{n(n+1)(n+2)}=$
初項から第$n$項までの和を求めよ
出典：同志社大学 過去問
群馬大・津田塾大 数列の和・積分 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B#津田塾大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
群馬大学過去問題
$a_k= \frac{(3k+1)(3k+2)}{3k(k+1)}$ (k自然数)
$\displaystyle\sum_{k=1}^n a_k$をnの式で
津田塾大学過去問題
$C:y=x^2-x-4|x-1|$と直線lは2点で接する。
Cとlで囲まれた面積
この動画を見る
群馬大学過去問題
$a_k= \frac{(3k+1)(3k+2)}{3k(k+1)}$ (k自然数)
$\displaystyle\sum_{k=1}^n a_k$をnの式で
津田塾大学過去問題
$C:y=x^2-x-4|x-1|$と直線lは2点で接する。
Cとlで囲まれた面積
北海道大 等比複素数列 高校数学 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
北海道大学過去問題
数列{$Z_n$}は初項48、公比$\frac{1}{4}(\sqrt{6}+\sqrt{2}i)$の等比複素数列である。
この数列の項のうち実数のみの項を並べた数列を{$a_n$}
(1)$Z_4$
(2)$a_3$
(3)$\displaystyle\sum_{n=1}^\infty a_n$
この動画を見る
北海道大学過去問題
数列{$Z_n$}は初項48、公比$\frac{1}{4}(\sqrt{6}+\sqrt{2}i)$の等比複素数列である。
この数列の項のうち実数のみの項を並べた数列を{$a_n$}
(1)$Z_4$
(2)$a_3$
(3)$\displaystyle\sum_{n=1}^\infty a_n$
京都大学 確率 数列 融合問題 高校数学 Mathematics Japanese university entrance exam Kyoto University
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2005京都大学過去問題
1～ｎまでの番号のついてn枚($n \geqq 3$,自然数)から3枚取り出して小さい順に並べたときに等差数列になる確率を求めよ.
この動画を見る
2005京都大学過去問題
1～ｎまでの番号のついてn枚($n \geqq 3$,自然数)から3枚取り出して小さい順に並べたときに等差数列になる確率を求めよ.
九州大 Σの公式証明 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2010九州大学過去問題
以下の問いに答えよ。証明
(1)和$1+2+3+\cdots+n$をnの多項式で表せ
(2)和$1^2+2^2+3^2+\cdots+n^2$をnの多項式で表せ
(3)和$1^3+2^3+3^3+\cdots+n^3$をnの多項式で表せ
この動画を見る
2010九州大学過去問題
以下の問いに答えよ。証明
(1)和$1+2+3+\cdots+n$をnの多項式で表せ
(2)和$1^2+2^2+3^2+\cdots+n^2$をnの多項式で表せ
(3)和$1^3+2^3+3^3+\cdots+n^3$をnの多項式で表せ
早稲田 群数列の和 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
早稲田大学過去問題
k自然数 $a_k$は$\sqrt k$にもっとも近い整数
(例)$a_5=2,a_8=3,a_{20}=4$
(1)$\displaystyle\sum_{k=1}^{12}a_k=a_1+a_2+\cdots+a_{12}$
(2)$\displaystyle\sum_{k=1}^{1998}a_k=a_1+a_2+\cdots+a_{1998}$
この動画を見る
早稲田大学過去問題
k自然数 $a_k$は$\sqrt k$にもっとも近い整数
(例)$a_5=2,a_8=3,a_{20}=4$
(1)$\displaystyle\sum_{k=1}^{12}a_k=a_1+a_2+\cdots+a_{12}$
(2)$\displaystyle\sum_{k=1}^{1998}a_k=a_1+a_2+\cdots+a_{1998}$
秋田大（医）数列の和 Σ 高校数学 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
秋田大学過去問題
$\displaystyle\sum_{k=1}^n \frac{1}{k}(a_k+\frac{1}{k+1})=2^n+1-\frac{1}{n+1}$
(1)数列{$a_n$}の一般項をnを用いて表せ。
(2)$\displaystyle\sum_{k=1}^na_k$を求めよ。
この動画を見る
秋田大学過去問題
$\displaystyle\sum_{k=1}^n \frac{1}{k}(a_k+\frac{1}{k+1})=2^n+1-\frac{1}{n+1}$
(1)数列{$a_n$}の一般項をnを用いて表せ。
(2)$\displaystyle\sum_{k=1}^na_k$を求めよ。
横浜国大 整数問題 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
横浜国立大学過去問題
P素数、n自然数
$P^n$を分母とする既約分数で、0より大きく、1より小さいものの総和を$S_n$
$S_1,S_2,S_3$
$S_n$を求めよ。
この動画を見る
横浜国立大学過去問題
P素数、n自然数
$P^n$を分母とする既約分数で、0より大きく、1より小さいものの総和を$S_n$
$S_1,S_2,S_3$
$S_n$を求めよ。
東邦 横市（医）慶應 高校数学 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東邦大学過去問題
$2log_5x+log_5y=log_5(x^2+y+59)$を満たす整数x,y
横浜市立大学過去問題
$\displaystyle\sum_{k=1}^{2n}(-1)^{k-1}k^2$
慶応義塾大学過去問題
$x+y+z=28$を満たす非負整数の組(x,y,z)のうちZが偶数となる場合の個数
この動画を見る
東邦大学過去問題
$2log_5x+log_5y=log_5(x^2+y+59)$を満たす整数x,y
横浜市立大学過去問題
$\displaystyle\sum_{k=1}^{2n}(-1)^{k-1}k^2$
慶応義塾大学過去問題
$x+y+z=28$を満たす非負整数の組(x,y,z)のうちZが偶数となる場合の個数
秋田大 慶応大 ３次方程式 Σ 高校数学 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#複素数平面#数列#数列とその和（等差・等比・階差・Σ）#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#秋田大学#数B#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
秋田大学過去問題
$2x^3-3x^2+ax-1=0$の1つの解は$x=\frac{1}{2}$,他の解をα,βとしたとき、$α^{30}+β^{30}$の値
慶応義塾大学過去問題
$\displaystyle\sum_{k=1}^nk・2^{k+2}$の値をnで表せ
この動画を見る
秋田大学過去問題
$2x^3-3x^2+ax-1=0$の1つの解は$x=\frac{1}{2}$,他の解をα,βとしたとき、$α^{30}+β^{30}$の値
慶応義塾大学過去問題
$\displaystyle\sum_{k=1}^nk・2^{k+2}$の値をnで表せ
【旧作】群数列の解き方が13分で明確にわかる動画【数学B】
福田の一夜漬け数学〜相加平均・相乗平均の関係〜その証明の考察５（受験編）
単元：
#数Ⅰ#数Ⅱ#数と式#式と証明#式の計算（整式・展開・因数分解）#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#数列#数列とその和（等差・等比・階差・Σ）#数学的帰納法#微分とその応用#色々な関数の導関数#接線と法線・平均値の定理#関数の変化（グラフ・最大最小・方程式・不等式）#数学(高校生)#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$n$個の正の数$a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}\\$
この動画を見る
$n$個の正の数$a_1,a_2,\cdots,a_n$に対して
$\displaystyle \frac{a_1+a_2+\cdots+a_n}{n}$$ \geqq \sqrt[n]{a_1a_2\cdots a_n}\\$
慶應（医）数列 高校数学 Japanese university entrance exam questions
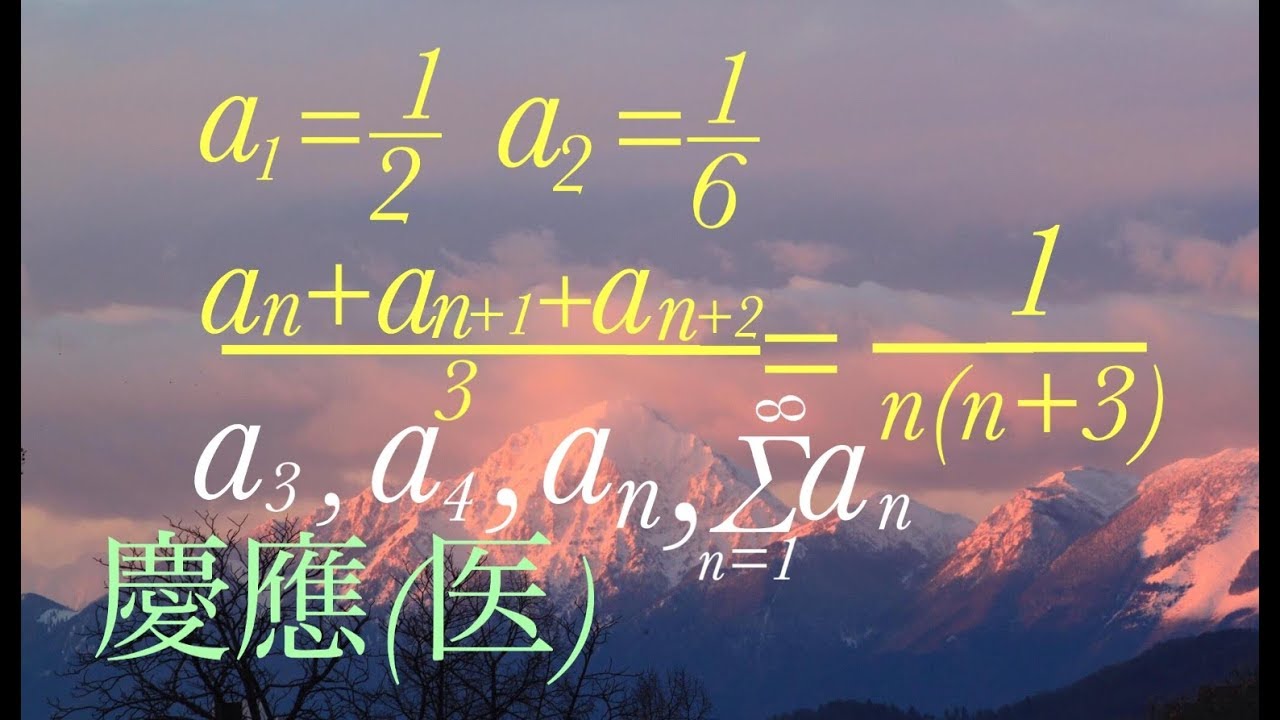
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
慶応義塾大学過去問題
数列$\{ a_n \}$の項の間に次の関係がある。
$a_1=\frac{1}{2},a_2=\frac{1}{6}$
$\frac{a_n+a_{n+1}+a_{n+2}}{3} = \frac{1}{n(n+3)}$
$n=1,2,3\cdots$
$a_3,a_4,a_n,\displaystyle\sum_{k=1}^\infty a_n$を求めよ。
この動画を見る
慶応義塾大学過去問題
数列$\{ a_n \}$の項の間に次の関係がある。
$a_1=\frac{1}{2},a_2=\frac{1}{6}$
$\frac{a_n+a_{n+1}+a_{n+2}}{3} = \frac{1}{n(n+3)}$
$n=1,2,3\cdots$
$a_3,a_4,a_n,\displaystyle\sum_{k=1}^\infty a_n$を求めよ。
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#三角関数#三角関数とグラフ#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#和歌山大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
福田の一夜漬け数学〜数列・漸化式(6)その他色々〜高校2年生
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
この動画を見る
次の漸化式を解け。(すべて$a_1=1$とする)
①$a_{n+1}=\displaystyle \frac{a_n}{4a_n-1}$
②$a_{n+1}=2\displaystyle \sqrt{a_n}$
③$a_{n+1}=2(n+1)a_n$
④$a_{n+1}=\displaystyle \frac{4a_n+8}{a_n+6}$
福田の一夜漬け数学〜数列・漸化式(5)連立漸化式〜高校2年生
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=4a_n+b_n\\
b_{n+1}=a_n+4b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=2\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_{n+1}=a_n+4b_n\\
b_{n+1}=a_n+b_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1\\
b_1=1\\
\end{array}
\right.
\end{eqnarray}$
福田の一夜漬け数学〜数列・漸化式(4)3項間の漸化式〜高校2年生
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
この動画を見る
次の漸化式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=5a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=1, a_2=5\\
a_{n+2}=4a_{n+1}-4a_n\\
\end{array}
\right.
\end{eqnarray}$
福田の一夜漬け数学〜数列・漸化式(3)〜高校2年生
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$
この動画を見る
次の漸化式を解け。(すべて、$a_1=1$とする)
①$(n+1)a_{n+1}=na_n+2$
②$na_{n+1}=(n+1)a_n+2$
③$(n+2)a_{n+1}=na_n+2$
④$na_{n+1}=(n+2)a_n+2$