 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
 数列とその和(等差・等比・階差・Σ)
数列とその和(等差・等比・階差・Σ)
福田の数学〜上智大学2024TEAP利用型理系第4問〜漸化式と証明

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の漸化式 $(\mathrm{A})$ を満たす数列 $\{ a_n\}$ を考える。
$(\mathrm{A}):$$a_{n+2}=na_{n+1}-a_n$$ \quad (n=1.2.3.\cdots)$
(1) $(\mathrm{A})$ を満たす数列を $1$つあげよ。
(2) $2$ つの数列 $\{ a_n\}$ と $\{ b_n\}$ が $(\mathrm{A})$ を満たすとする。どんな実数 $x,y$ に対しても数列 $\{ xa_n + yb_n \}$ が $(\mathrm{A})$ を満たすことを証明せよ。
この動画を見る
次の漸化式 $(\mathrm{A})$ を満たす数列 $\{ a_n\}$ を考える。
$(\mathrm{A}):$$a_{n+2}=na_{n+1}-a_n$$ \quad (n=1.2.3.\cdots)$
(1) $(\mathrm{A})$ を満たす数列を $1$つあげよ。
(2) $2$ つの数列 $\{ a_n\}$ と $\{ b_n\}$ が $(\mathrm{A})$ を満たすとする。どんな実数 $x,y$ に対しても数列 $\{ xa_n + yb_n \}$ が $(\mathrm{A})$ を満たすことを証明せよ。
霊感強い系の受験者は、山勘でいける 関西医科大学2024 大学入試問題#933

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師:
ますただ
問題文全文(内容文):
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3・・・)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
この動画を見る
数列$\{an\}$を
$a_1=2,a_{n+1}=S_n-n(n-4)$
$(n=1,2,3・・・)$で定めるとき,$a_n$と$S_n$を
それぞれ$n$の式で表せ.
2024関西医科大学過去問題
福田のおもしろ数学252〜平方数であることの証明

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$49,4489,444889,…,444…48…89,…$はすべて平方数である。証明せよ。
この動画を見る
$49,4489,444889,…,444…48…89,…$はすべて平方数である。証明せよ。
大学入試問題#923「帰納法で解いても良いのかな」

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
この動画を見る
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
百マス計算全部出したらなんぼ?

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
「百マス計算全部出したらいくつか」について解説しています。
この動画を見る
「百マス計算全部出したらいくつか」について解説しています。
2025年度入試に出るかも?~答えが2025になる計算問題~

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2025年度入試に出るかも?
「答えが2025になる計算問題」について解説しています。
※問題文は動画内参照
この動画を見る
2025年度入試に出るかも?
「答えが2025になる計算問題」について解説しています。
※問題文は動画内参照
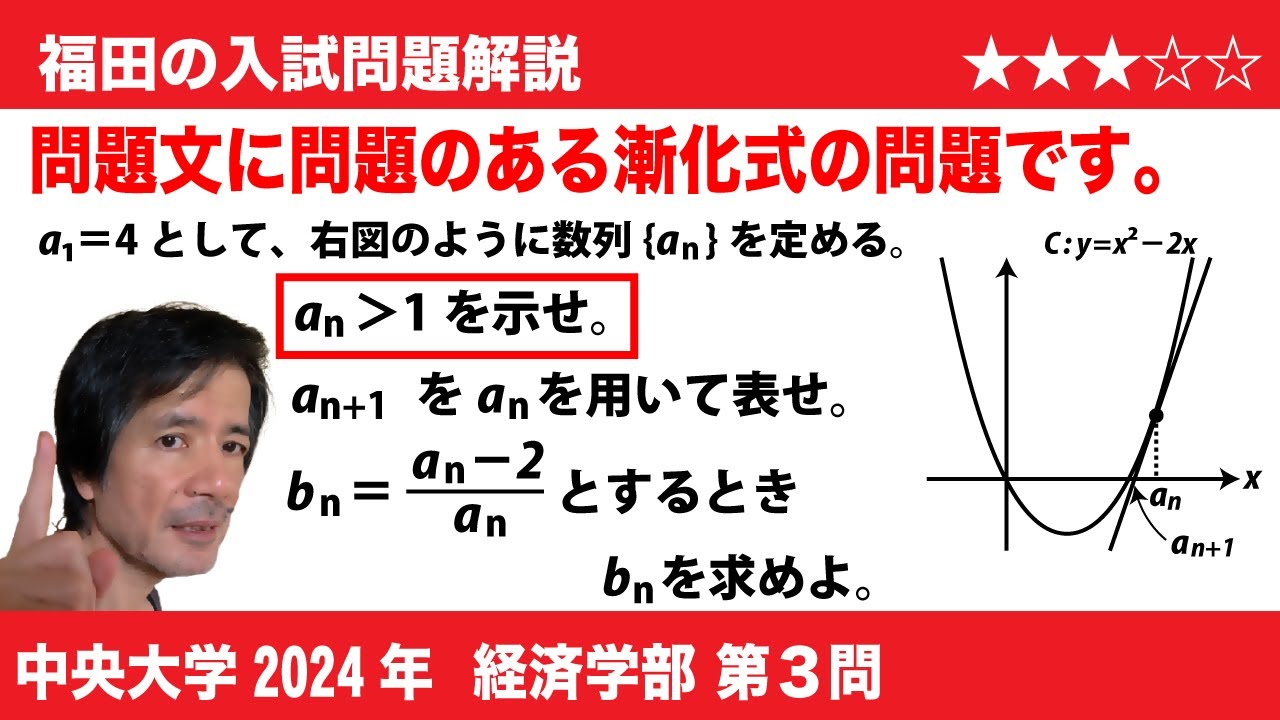
福田の数学〜中央大学2024経済学部第3問〜数列と漸化式
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
3.
座標平面上に曲線 $C$ : $y = x ^ 2 - 2x$ がある。$C$上の点$P_n (a_n, a_n²-2a_n) \ ( n = 1 , 2, 3, ・・・) $について、 $a_{1} = 4$ とし、 $a_{n + 1}$ は$C$の$P_n$における接線と$x$軸との交点の$x$座標であるとする。このとき、$a_n$は$1$より大きいことが分かっている。以下の設問に答えよ。
(1) $a_{n+ 1}$を$a_n$を用いて表せ。
(2) $b_{n}= \dfrac{a_n-2}{a_n}$とするとき、 $b_{n+ 1}$ を$b_n$を用いて表せ。
(3) $b_n$を$n$を用いて表せ。
この動画を見る
3.
座標平面上に曲線 $C$ : $y = x ^ 2 - 2x$ がある。$C$上の点$P_n (a_n, a_n²-2a_n) \ ( n = 1 , 2, 3, ・・・) $について、 $a_{1} = 4$ とし、 $a_{n + 1}$ は$C$の$P_n$における接線と$x$軸との交点の$x$座標であるとする。このとき、$a_n$は$1$より大きいことが分かっている。以下の設問に答えよ。
(1) $a_{n+ 1}$を$a_n$を用いて表せ。
(2) $b_{n}= \dfrac{a_n-2}{a_n}$とするとき、 $b_{n+ 1}$ を$b_n$を用いて表せ。
(3) $b_n$を$n$を用いて表せ。
福田のおもしろ数学220〜二項係数のシグマ計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\sum^{20}_{k=5} {}_{k}\mathrm{C}_{4}$ を計算して下さい。
この動画を見る
$\displaystyle\sum^{20}_{k=5} {}_{k}\mathrm{C}_{4}$ を計算して下さい。
大学入試問題#895「2番だけで良い大問」 #福井大学医学部(2015) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
この動画を見る
$a_1=2$
$3a_{n+1}-4a_n+1=0$
1.数列{$a_n$}の一般項を求めよ。
2.$\displaystyle \frac{a_{n+1}}{a_n}$の小数部分を$b_n$とし、数列{$b_n$}の一般項を求めよ。
3.$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{b_k}$を求めよ。
出典:2015年福井大学医学部
福田の数学〜千葉大学2024年理系第9問〜漸化式と極限

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
この動画を見る
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
これ解ける?

単元:
#算数(中学受験)#計算と数の性質#数列#数列とその和(等差・等比・階差・Σ)#規則性(周期算・方陣算・数列・日暦算・N進法)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これ解ける?
※問題文は動画内参照
この動画を見る
これ解ける?
※問題文は動画内参照
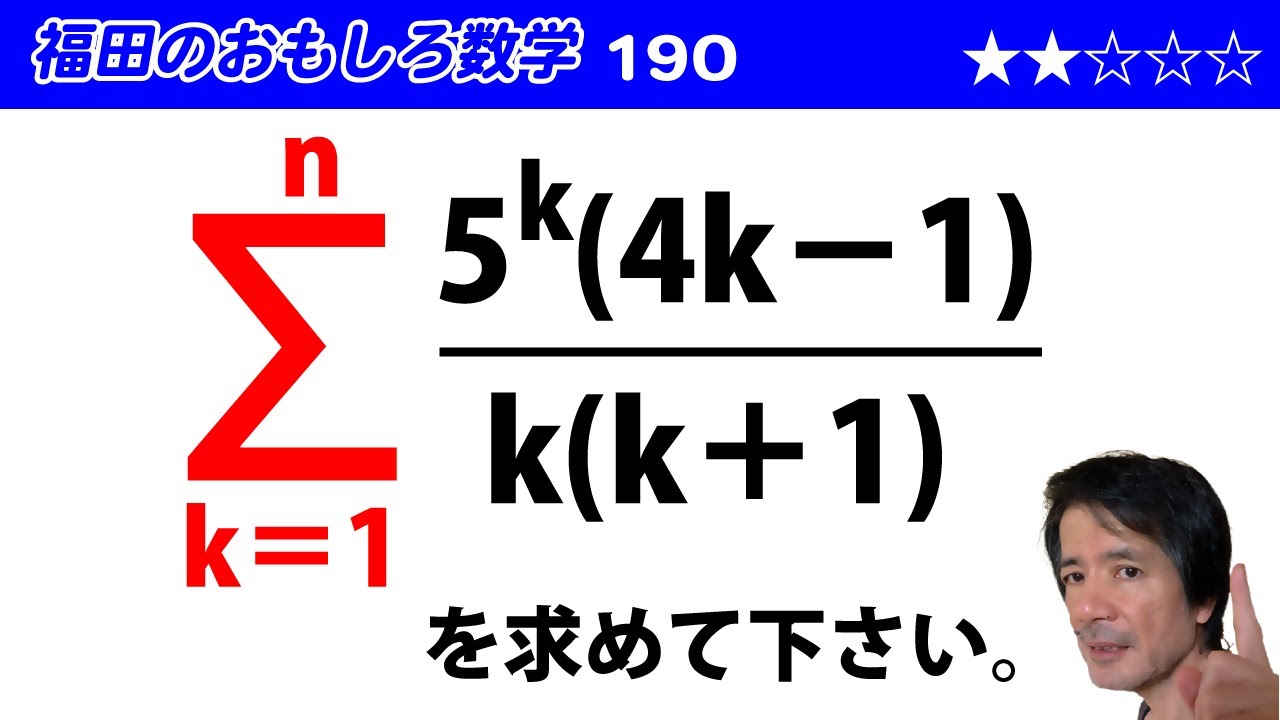
福田のおもしろ数学190〜数列の和と部分分数分解
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n \frac {5^k(4k-1)}{k(k+1)}$を求めよ。
この動画を見る
$\displaystyle \sum_{k=1}^n \frac {5^k(4k-1)}{k(k+1)}$を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第3問〜指数関数で定義された数列の漸化式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
この動画を見る
$\Large{\boxed{3}}$ 実数$a$に対して$f(a)$=$\displaystyle\frac{1}{2}(2^a-2^{-a})$とおく。また、$A$=$2^a$とする。
(1)等式$\displaystyle\left(A-\frac{1}{A}\right)^3$=$\displaystyle\boxed{\ \ ア\ \ }\left(A-\frac{1}{A}\right)^3$-$\displaystyle\boxed{\ \ イ\ \ }\left(A-\frac{1}{A}\right)$ より、実数$a$に対して
$\left\{f(a)\right\}^3$=$\frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}f(3a)$-$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}f(a)$ ...①が成り立つ。
(2)実数$a$,$b$に対して$f(a)$=$b$が成り立つならば、$A$=$2^a$は2次方程式
$A^2$-$\boxed{\ \ キ\ \ }bA$-$\boxed{\ \ ク\ \ }$=0
を満たす。$2^a$>0より、$a$は$b$を用いて
$a$=$\log_2\left(\boxed{\ \ ケ\ \ }b+\sqrt{b^2+\boxed{\ \ コ\ \ }}\right)$ ...②
と表せる。つまり、任意の実数bに対して$f(a)$=$b$となる実数$a$が、ただ1つに定まる。
以下、数列$\left\{a_n\right\}$に対して$f(a_n)$=$b_n$ ($n$=1,2,3,...)で定まる数列$\left\{b_n\right\}$が、関係式
$4b_{n+1}^3$+$3b_{n+1}$-$b_n$=0 ($n$=1,2,3,...) ...③
を満たすとする。
(3)①と③から$f\left(\boxed{\ \ サ\ \ }a_{n+1}\right)$=$f(a_n)$ ($n$=1,2,3,...)となるので、(2)より、
$a_n$=$\displaystyle\frac{a_1}{\boxed{\ \ シ\ \ }^{n-p}}$ ($n$=1,2,3,...)が得られる。ここで、$p$=$\boxed{\ \ ス\ \ }$である。
(4)$n$≧2に対して、$S_n$=$\displaystyle\sum_{k=2}^n3^{k-1}b_k^3$ とおく。$c_n$=$3^nb_n$ ($n$=1,2,3,...)で定まる数列$\left\{c_n\right\}$の階差数列を用いると、③より、
$S_n$=$\frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}b_1$-$\frac{\boxed{\ \ タ\ \ }^n}{\boxed{\ \ チ\ \ }}b_n$ ($n$=2,3,4,...)
となる。ゆえに、$b_1$=$\displaystyle\frac{4}{3}S_5$-108 が成り立つならば$a_1$=$\boxed{\ \ ツテト\ \ }\log_2\boxed{\ \ ナ\ \ }$ である。
大学入試問題#862「計算力と根性!」 #京都大学(2023) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=3 \\
a_n=\displaystyle \frac{S_n}{n}+(n-1)・2^n
\end{array}
\right.
\end{eqnarray}$
を満たすような数列$\{a_n\}$の一般項を求めよ
出典:2023年京都大学 入試問題
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=3 \\
a_n=\displaystyle \frac{S_n}{n}+(n-1)・2^n
\end{array}
\right.
\end{eqnarray}$
を満たすような数列$\{a_n\}$の一般項を求めよ
出典:2023年京都大学 入試問題
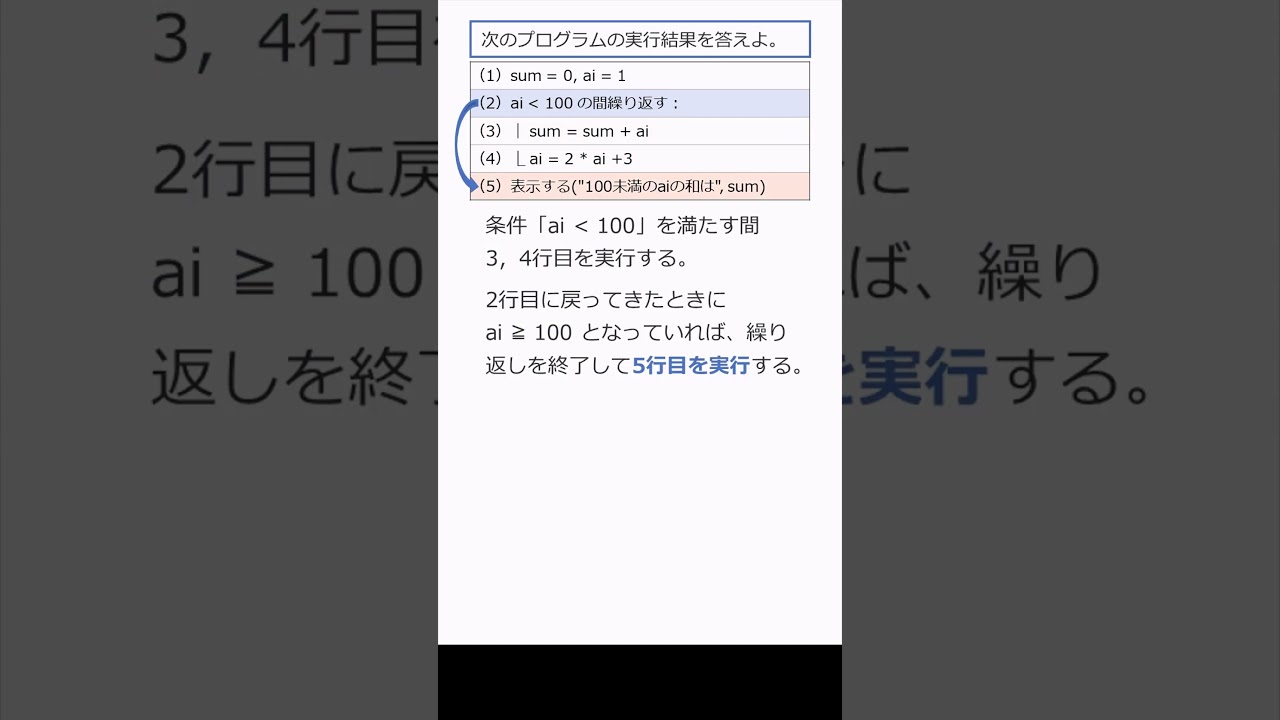
288 数列の100以下の項を足し合わせる:漸化式とΣの面倒な問題もプログラムで楽々解決! #shorts
単元:
#情報Ⅰ(高校生)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#プログラミング#プログラムによる動的シミュレーション#数B
指導講師:
めいちゃんねる
問題文全文(内容文):
288 数列の100以下の項を足し合わせる:漸化式とΣの面倒な問題もプログラムで楽々解決! #shorts
【問題文】次のプログラムの実行結果を答えよ。
※プログラムは動画内参照
この動画を見る
288 数列の100以下の項を足し合わせる:漸化式とΣの面倒な問題もプログラムで楽々解決! #shorts
【問題文】次のプログラムの実行結果を答えよ。
※プログラムは動画内参照
福田の数学〜神戸大学2024年理系第1問〜無理関数を利用して定義された数列の一般項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
福田の数学〜大阪大学2024年文系第3問〜素数を小さい順に並べた数列の特徴

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 素数を小さい順に並べて得られる数列を
$p_1$, $p_2$, ..., $p_n$, ...
とする。
(1)$p_{15}$の値を求めよ。
(2)$n$≧12のとき、不等式$p_n$>$3n$が成り立つことを示せ。
この動画を見る
$\Large\boxed{3}$ 素数を小さい順に並べて得られる数列を
$p_1$, $p_2$, ..., $p_n$, ...
とする。
(1)$p_{15}$の値を求めよ。
(2)$n$≧12のとき、不等式$p_n$>$3n$が成り立つことを示せ。
福田のおもしろ数学138〜シグマ計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\sum_{k=1}^nk(k!)$ を求めよ。
この動画を見る
$\displaystyle\sum_{k=1}^nk(k!)$ を求めよ。
福田の数学〜一橋大学2024年文系第1問〜シグマが2024になるような2変数の値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
この動画を見る
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
福田の数学〜東北大学2024年文系第4問〜連立漸化式と不定方程式の整数解

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
福田の数学〜慶應義塾大学2024年看護医療学部第3問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
福田のおもしろ数学095〜素数が並ぶ数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
この動画を見る
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
福田の数学〜慶應義塾大学2024年薬学部第1問(1)〜等差数列と等比中項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
難解な数列の問題 By 英語orドイツ語シはBかHか さん

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_0=b_0=1$
$a_{n+1}=\displaystyle \frac{a_n}{a_n^2+b_n^2}$
$b_{n+1}=2-\displaystyle \frac{b_n}{a_n^2+b_n^2}$
一般項$a_n,b_n$を求めよ。
この動画を見る
$a_0=b_0=1$
$a_{n+1}=\displaystyle \frac{a_n}{a_n^2+b_n^2}$
$b_{n+1}=2-\displaystyle \frac{b_n}{a_n^2+b_n^2}$
一般項$a_n,b_n$を求めよ。
福田のおもしろ数学051〜10秒チャレンジ!〜階乗の付いた分数の計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
この動画を見る
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
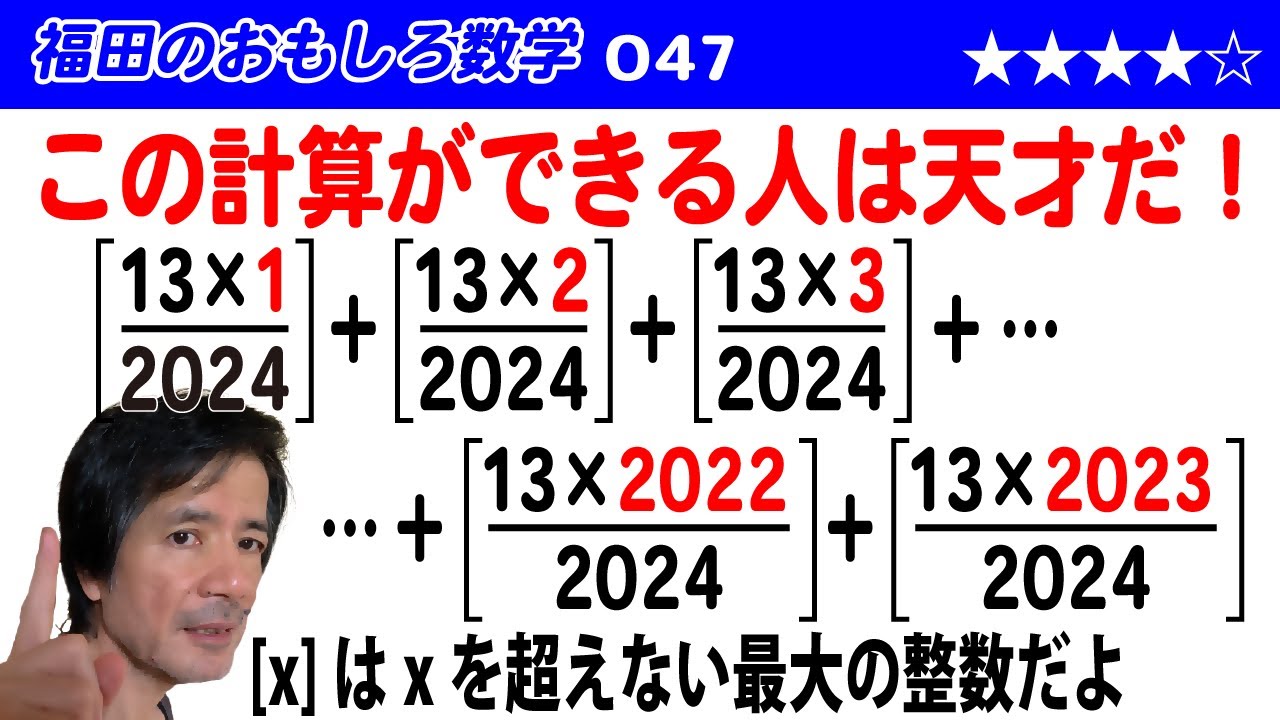
福田のおもしろ数学047〜これができたら天才〜ガウス記号のついた数の和
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left[\dfrac{13×1}{2024}\right]+\left[\dfrac{13×2}{2024}\right]+\left[\dfrac{13×3}{2024}\right]+・・・+\left[\dfrac{13×2023}{2024}\right]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
この動画を見る
$\left[\dfrac{13×1}{2024}\right]+\left[\dfrac{13×2}{2024}\right]+\left[\dfrac{13×3}{2024}\right]+・・・+\left[\dfrac{13×2023}{2024}\right]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
数列 by ハルハルさん すげー解答: 英語orドイツ語さん #Shorts

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
この動画を見る
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
2024年共通テスト徹底解説〜数学ⅡB第4問数列〜福田の入試問題解説

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
数列 難易度高め by Picmin3daisukiさん #Shorts

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
数列 By Picmin3daisukiさん

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
