 複素数平面
複素数平面
 複素数平面
複素数平面
虚数単位の入った漸化式 学習院大

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数C#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2019学習院大学過去問題
$Z_1=1$
$Z_{n+1}=iZ_n+2$
(1)$Z_{2019}$
(2)$Z_n$が通る円の中心と半径
この動画を見る
2019学習院大学過去問題
$Z_1=1$
$Z_{n+1}=iZ_n+2$
(1)$Z_{2019}$
(2)$Z_n$が通る円の中心と半径
福田の数学〜筑波大学2023年理系第6問〜複素数平面上の点の軌跡とアポロニウスの円

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{6}$ $i$を虚数単位とする。複素数平面に関する以下の問いに答えよ。
(1)等式|$z$+2|=2|$z$-1| を満たす点$z$の全体が表す図形は円であることを示し、その中心と半径を求めよ。
(2)等式
$\left\{|z+2|-2|z-1|\right\}$$|z+6i|$=$3\left\{|z+2|-2|z-1|\right\}$$|z-2i|$
を満たす点$z$の全体が表す図形をSとする。このときSを複素数平面上に図示せよ。
(3)点$z$が(2)における図形S上を動くとき、$w$=$\frac{1}{z}$ で定義される点$w$が描く図形を複素数平面上に図示せよ。
2023筑波大学理系過去問
福田の数学〜九州大学2023年理系第1問〜複素数平面上の三角形の形状

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)4次方程式$x^4$-2$x^3$+3$x^2$-2$x$+1=0 を解け。
(2)複素数平面上の$\triangle$ABCの頂点を表す複素数をそれぞれ$\alpha$, $\beta$, $\gamma$とする。
$(\alpha-\beta)^4$+$(\beta-\gamma)^4$+$(\gamma-\alpha)^4=0$
が成り立つとき、$\triangle$ABCはどのような三角形になるか答えよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)4次方程式$x^4$-2$x^3$+3$x^2$-2$x$+1=0 を解け。
(2)複素数平面上の$\triangle$ABCの頂点を表す複素数をそれぞれ$\alpha$, $\beta$, $\gamma$とする。
$(\alpha-\beta)^4$+$(\beta-\gamma)^4$+$(\gamma-\alpha)^4=0$
が成り立つとき、$\triangle$ABCはどのような三角形になるか答えよ。
2023九州大学理系過去問
【短時間でマスター!!】複素数の計算を解説!〔現役講師解説、数学〕

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
3rd School
問題文全文(内容文):
数学2B
①$(3-2i)+(2+5i)$
②$(3-2i)-(2+5i)$
③$(3-2i)(2+5i)$
$a+bi$の形にせよ。
①$\frac{1+3i}{3+i}$
②$\frac{1+2i}{3i}$
この動画を見る
数学2B
①$(3-2i)+(2+5i)$
②$(3-2i)-(2+5i)$
③$(3-2i)(2+5i)$
$a+bi$の形にせよ。
①$\frac{1+3i}{3+i}$
②$\frac{1+2i}{3i}$
福田の数学〜名古屋大学2023年理系第1問〜4次方程式の解と共役な複素数の性質

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#名古屋大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 実数係数の4次方程式$x^4$$-px^3$$+qx^2$$-rx$$+s$=0 は相異なる複素数$\alpha$, $\bar{\alpha}$, $\beta$, $\bar{\beta}$を解に持ち、点1を中心とする半径1の円周上にあるとする。ただし、$\bar{\alpha}$, $\bar{\beta}$はそれぞれ $\alpha$, $\beta$と共役な複素数を表す。
(1)$\alpha$+$\bar{\alpha}$=$\alpha$$\bar{\alpha}$ を示せ。
(2)$t$=$\alpha$+$\bar{\alpha}$, $u$=$\beta$+$\bar{\beta}$とおく。p, q, r, sをそれぞれtとuで表せ。
(3)座標平面において、点(p, s)のとりうる範囲を図示せよ。
2023名古屋大学理系過去問
福田の数学〜東北大学2023年理系第4問〜1の5乗根

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{4}$ 実数a=$\frac{\sqrt5-1}{2}$に対して、整式f(x)=$x^2$-$ax$+1を考える。
(1)整式$x^4$+$x^3$+$x^2$+$x$+1 はf(x)で割り切れることを示せ。
(2)方程式f(x)=0の虚数解であって虚部が正のものを$\alpha$とする。$\alpha$を極形式で表せ。ただし、$r^5$=1を満たす実数rがr=1のみであることは、認めて使用してよい。
(3)設問(2)の虚数$\alpha$に対して、$\alpha^{2023}$+$\alpha^{-2023}$の値を求めよ。
2023東北大学理系過去問
長崎大 複素数と整数の融合問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
この動画を見る
$m,n$を整数とする.
$\alpha=m+\sqrt7 ni$,
$\alpha^3=225+2\sqrt7 i$
(1)$x^3=1$を解け.
(2)$m,n$を求めよ.
(3)$Z^3=225+2\sqrt7 i$を解け.
長崎大過去問
大学入試問題#531「作成時間がありませんでした。」 横浜市立大学(2022) #複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\alpha^{18}+\alpha^6+\alpha^4+\alpha^2$の値を求めよ
出典:2023年横浜市立大学 入試問題
この動画を見る
$\alpha=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\alpha^{18}+\alpha^6+\alpha^4+\alpha^2$の値を求めよ
出典:2023年横浜市立大学 入試問題
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
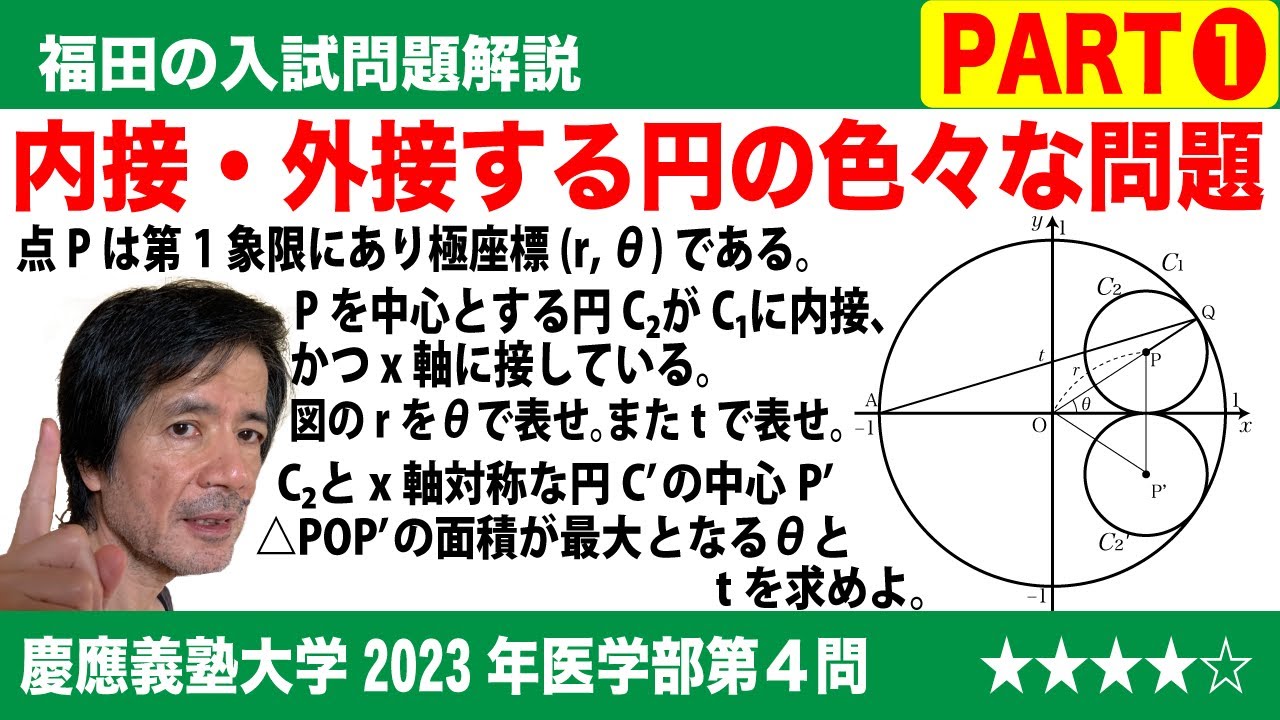
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第1問(2)〜虚数が係数の2次方程式の解

単元:
#大学入試過去問(数学)#2次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)式4$z^2$+4$z$-$\sqrt 3 i$=0を満たす複素数zは2つある。それらを$\alpha$,$\beta$とする。ただし、$i$は虚数単位である。$\alpha$,$\beta$に対応する複素数平面上の点をそれぞれP,Qとすると、線分PQの長さは$\boxed{\ \ え\ \ }$であり、PQの中点の座標は($\boxed{\ \ お\ \ }$, $\boxed{\ \ か\ \ }$)である。
また線分PQの垂直二等分線の傾きは$\boxed{\ \ き\ \ }$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (2)式4$z^2$+4$z$-$\sqrt 3 i$=0を満たす複素数zは2つある。それらを$\alpha$,$\beta$とする。ただし、$i$は虚数単位である。$\alpha$,$\beta$に対応する複素数平面上の点をそれぞれP,Qとすると、線分PQの長さは$\boxed{\ \ え\ \ }$であり、PQの中点の座標は($\boxed{\ \ お\ \ }$, $\boxed{\ \ か\ \ }$)である。
また線分PQの垂直二等分線の傾きは$\boxed{\ \ き\ \ }$である。
2023慶應義塾大学医学部過去問
神戸大 3次方程式の基本問題
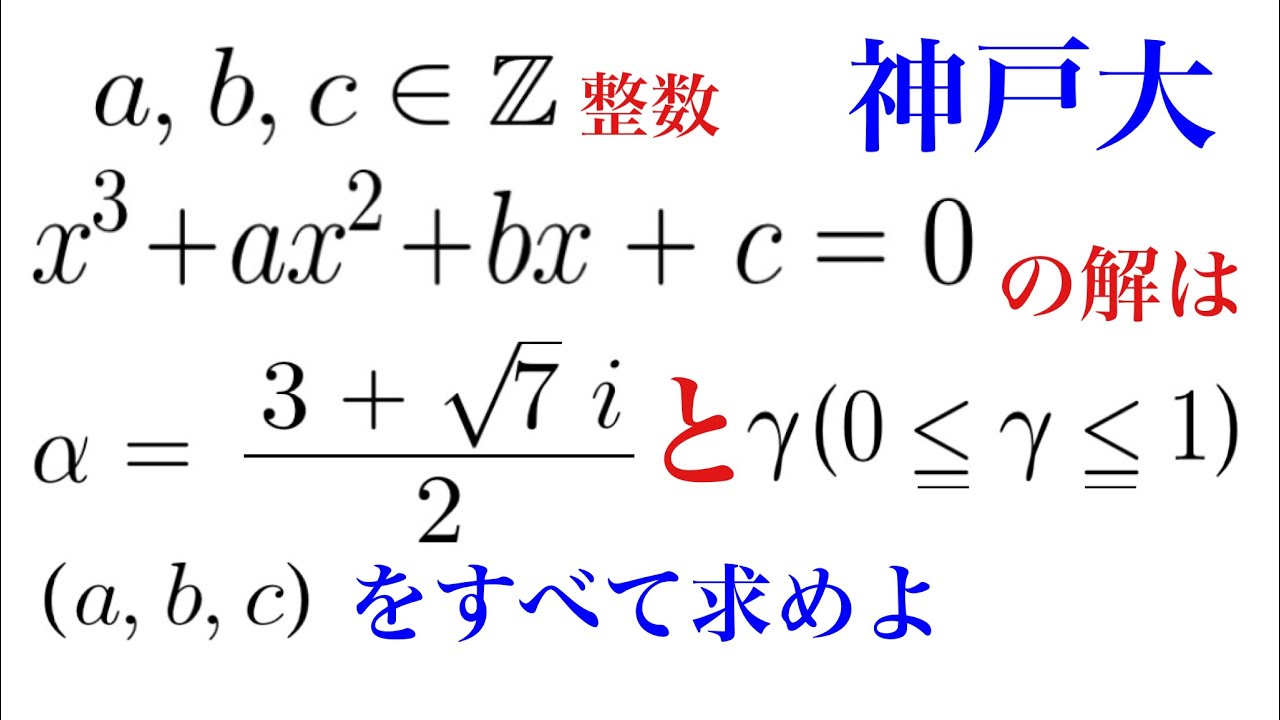
単元:
#数Ⅰ#数Ⅱ#数と式#複素数と方程式#複素数平面#一次不等式(不等式・絶対値のある方程式・不等式)#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
この動画を見る
$a,b,c$は整数である。
$x^3+ax^2+bx+c=0$は$\alpha=\dfrac{3+\sqrt{7}i}{2}$と0以上1以下の解をもつ(a,b,c)をすべて求めよ.
神戸大過去問
福田の数学〜早稲田大学2023年理工学部第4問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#微分とその応用#複素数平面#図形への応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
この動画を見る
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
東海大(医)虚数の回転

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東海大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{13}{12}\pi+i\sin\dfrac{13}{12}\pi$を$a+bi$を中心に$\dfrac{\pi}{6}$回転すると,
$\cos\dfrac{17}{12}\pi+i\sin\dfrac{17}{12}\pi$となる.
実数$a,b$を求めよ.
東海大(医)過去問
この動画を見る
$\cos\dfrac{13}{12}\pi+i\sin\dfrac{13}{12}\pi$を$a+bi$を中心に$\dfrac{\pi}{6}$回転すると,
$\cos\dfrac{17}{12}\pi+i\sin\dfrac{17}{12}\pi$となる.
実数$a,b$を求めよ.
東海大(医)過去問
福田の数学〜北海道大学2023年理系第1問〜複素数平面上の図形の列

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
藤田医科大 複素数の基本問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=1-\sqrt{3}i$
$Z^7+aZ^5-b=0$が成り立つ実数$a,b$を求めよ.
藤田医科大過去問
この動画を見る
$Z=1-\sqrt{3}i$
$Z^7+aZ^5-b=0$が成り立つ実数$a,b$を求めよ.
藤田医科大過去問
基本問題
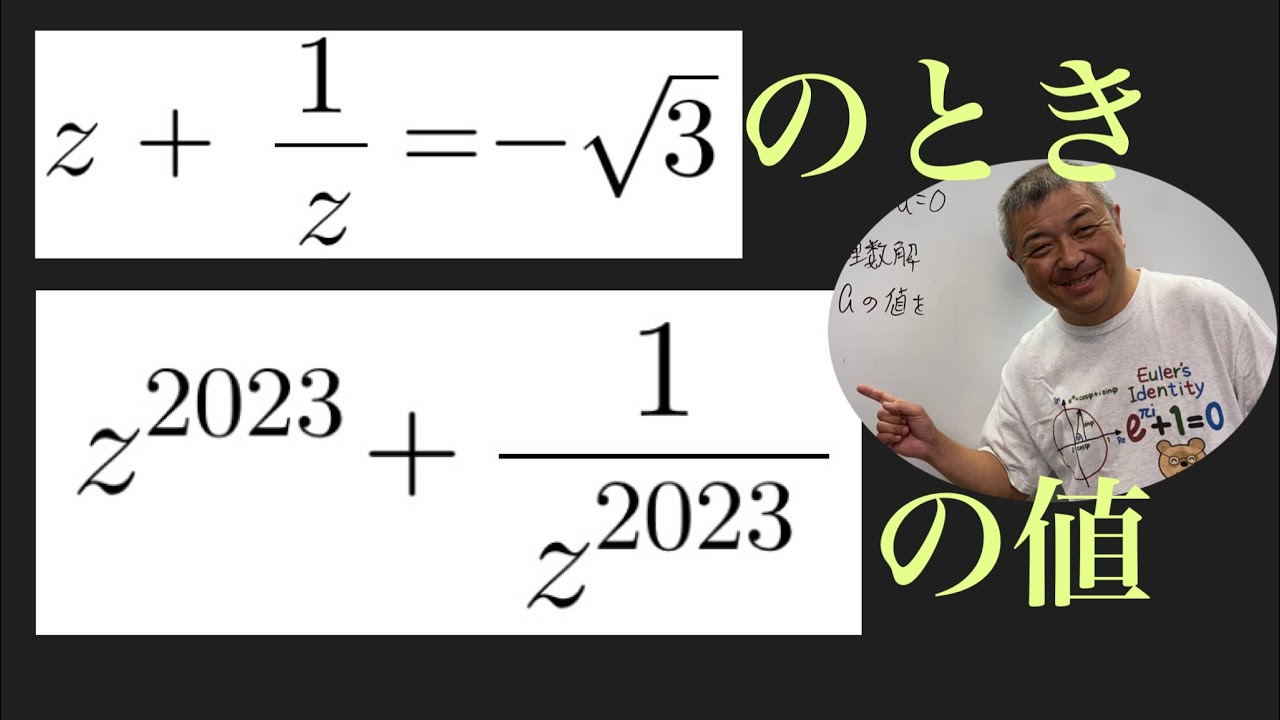
単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z+\dfrac{1}{Z}=-\sqrt{3}$のとき,
$Z^{2023}+\dfrac{1}{Z^{2023}}$の値を求めよ。
この動画を見る
$Z+\dfrac{1}{Z}=-\sqrt{3}$のとき,
$Z^{2023}+\dfrac{1}{Z^{2023}}$の値を求めよ。
2023久留米大(医)複素数の計算

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
複素数Zは$\vert Z \vert =1$で$Z^2-2Z+\dfrac{1}{Z}$が純虚数であるZの値を求めよ。
久留米大(医)過去問
この動画を見る
複素数Zは$\vert Z \vert =1$で$Z^2-2Z+\dfrac{1}{Z}$が純虚数であるZの値を求めよ。
久留米大(医)過去問
2023藤田医科大 1の7乗根の基本問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$Z=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\piのとき
Z^7=\Box
Z^6+Z^5+Z^4+Z^3+Z^2+Z=\Box
(1-Z)(1-Z^2)(1-Z^3)×(1-Z^4)(1-Z^5)(1-Z^6)=\Box
\Boxを答えよ.$
この動画を見る
$Z=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\piのとき
Z^7=\Box
Z^6+Z^5+Z^4+Z^3+Z^2+Z=\Box
(1-Z)(1-Z^2)(1-Z^3)×(1-Z^4)(1-Z^5)(1-Z^6)=\Box
\Boxを答えよ.$
【数ⅢC】 複素数平面の基本⑬3点が一直線上にあるとき、なす角が垂直のときを考える

【数ⅢC】 複素数平面の基本⑫半直線のなす角を考える

【数ⅢC】 複素数平面の基本⑪図形の方程式を条件から考える

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
点zが原点Oを中心とする半径2の円上を動くとき、$w=\dfrac{z-2}{z+1}$はどのような図形を描くか
この動画を見る
点zが原点Oを中心とする半径2の円上を動くとき、$w=\dfrac{z-2}{z+1}$はどのような図形を描くか
【数ⅢC】 複素数平面の基本⑩円の方程式を条件から考える

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を満たす点z全体はどのような図形を表すか
$\vert z+1\vert=2\vert z-2\vert$
この動画を見る
次の方程式を満たす点z全体はどのような図形を表すか
$\vert z+1\vert=2\vert z-2\vert$
福田の数学〜東京工業大学2023年理系第3問〜複素数の絶対値と偏角に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#漸化式#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
【数ⅢC】複素数平面の基本⑨垂直二等分線を考える

【数ⅢC】複素数平面の基本⑧円の方程式を考える

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
円の方程式を考える
次の方程式で与えられる円の中心、半径を求めよ
(1)$\vert z+2i\vert=3$
(2)$\vert z+3-2i\vert =1$
(3)$\vert z-i\vert=1$
この動画を見る
円の方程式を考える
次の方程式で与えられる円の中心、半径を求めよ
(1)$\vert z+2i\vert=3$
(2)$\vert z+3-2i\vert =1$
(3)$\vert z-i\vert=1$
【数ⅢC】複素数平面の基本⑥1のn乗根をド・モアブルの定理で考える

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi$のとき、$z^4+z^3+z^2+z+1$の値を求めよ
この動画を見る
$z=\cos\dfrac{2}{5}\pi+i\sin\dfrac{2}{5}\pi$のとき、$z^4+z^3+z^2+z+1$の値を求めよ
【数ⅢC】複素数平面の基本⑤複素数の積・商の考え方

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数を極形式で表せ
$\cos\dfrac{2}{3}\pi-i\sin\dfrac{2}{3}\pi$
この動画を見る
次の複素数を極形式で表せ
$\cos\dfrac{2}{3}\pi-i\sin\dfrac{2}{3}\pi$
【数ⅢC】複素数平面の基本④複素数の極形式の単位円を用いた考え方

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数を極形式で表せ
$\cos\dfrac{2}{3}\pi-i\sin\dfrac{2}{3}\pi$
この動画を見る
次の複素数を極形式で表せ
$\cos\dfrac{2}{3}\pi-i\sin\dfrac{2}{3}\pi$
【数ⅢC】複素数平面の基本③複素数平面の極形式の裏ワザ

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数を極形式で表せ
(1)$\sqrt3+i$ (2)$-2+2i$
この動画を見る
次の複素数を極形式で表せ
(1)$\sqrt3+i$ (2)$-2+2i$
【数ⅢC】複素数平面の基本②複素数平面における絶対値の計算

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数の絶対値を求めよ
(1)$-3+4i$ (2)$(1-2i)^2$ (3)$\dfrac{2+3i}{5-i}$
2点$A(\alpha),B(\beta)$間の距離を求めよ
(1)$\alpha=3+4i,\beta=7+5i$ (2)$\alpha=-3i,\beta=5$
この動画を見る
次の複素数の絶対値を求めよ
(1)$-3+4i$ (2)$(1-2i)^2$ (3)$\dfrac{2+3i}{5-i}$
2点$A(\alpha),B(\beta)$間の距離を求めよ
(1)$\alpha=3+4i,\beta=7+5i$ (2)$\alpha=-3i,\beta=5$
