高校入試過去問(数学)
高校入試過去問(数学)
6つの小さい円と大きい円 2024城北高校
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#中３数学#三平方の定理#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
この動画を見る
半径が$1$cm, $2$cm, $3$cmの同心円。
半径$3$cmの円の弦が、半径$1$cmの円と点Rで接している。
弦の実線部分PQの長さは$\fbox{$\hskip5em\Rule{0pt}{0.8em}{0em}$}$cmである。
【数式に翻訳せよ…！】整数：新潟県～全国入試問題解法
単元：
#数学(中学生)#整数の性質#高校入試過去問(数学)#新潟県公立高校入試
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
この動画を見る
$ある連続する自然数n,mについて、以下が成立するとき(n,m)を求めよ$
$n*m+55=n+m$
【素早く、論理的に…！】整数：桃山学院高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
６つの整数、－５，－３、－１、２，４，６のうち、異なる４つを選び、以下の計算式に入れる。
A×B+（C／Ｄ）
この計算結果の最大値を求めなさい。
この動画を見る
６つの整数、－５，－３、－１、２，４，６のうち、異なる４つを選び、以下の計算式に入れる。
A×B+（C／Ｄ）
この計算結果の最大値を求めなさい。
【正解への最短経路…！】平方根：京都女子高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
1/260{(3√30+√10-3√15+√5)²-(3√30+√10)²-(3√15-√5)²}計算せよ
この動画を見る
1/260{(3√30+√10-3√15+√5)²-(3√30+√10)²-(3√15-√5)²}計算せよ
【数式に翻訳せよ…！】整数：新潟県～全国入試問題解法
単元：
#数学(中学生)#数A#整数の性質#高校入試過去問(数学)#数学(高校生)#新潟県公立高校入試
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ある連続する2つの自然数n,mについて、n+m+55 = nm である$
この動画を見る
$ある連続する2つの自然数n,mについて、n+m+55 = nm である$
【公式なんてイラナイ…!?】整数：ノートルダム女学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#中３数学#正の数・負の数#方程式#２次方程式#文字と式#高校入試過去問(数学)#ノートルダム女学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
29=a²+b²+c²
上の式に入る正の整数の組(a,b,c)を答えなさい
ただし、a≦b≦cとします
この動画を見る
29=a²+b²+c²
上の式に入る正の整数の組(a,b,c)を答えなさい
ただし、a≦b≦cとします
【一発で理解できる…！】平方根：福岡女学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
3<√n<2√5
を満たす自然数の個数を求めよ
この動画を見る
3<√n<2√5
を満たす自然数の個数を求めよ
【まるで大学入試…！】因数分解：早稲田大学本庄高等学院～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
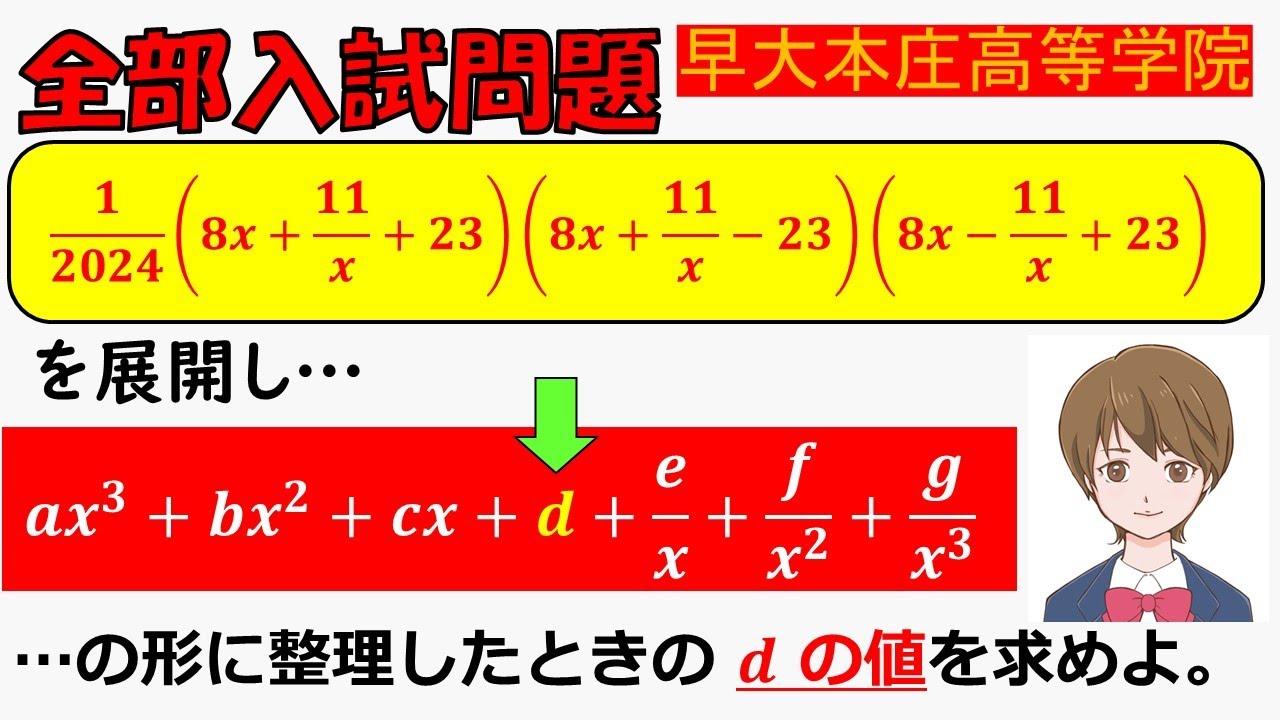
1/2024(8x+11/x+23)(8x+11/x-23)(8x-11/x+23)
を展開しax³+bx²+cx+d+e/x+f/x²+g/x³
…の形に整理した時のdの値を求めよ
この動画を見る
1/2024(8x+11/x+23)(8x+11/x-23)(8x-11/x+23)
を展開しax³+bx²+cx+d+e/x+f/x²+g/x³
…の形に整理した時のdの値を求めよ
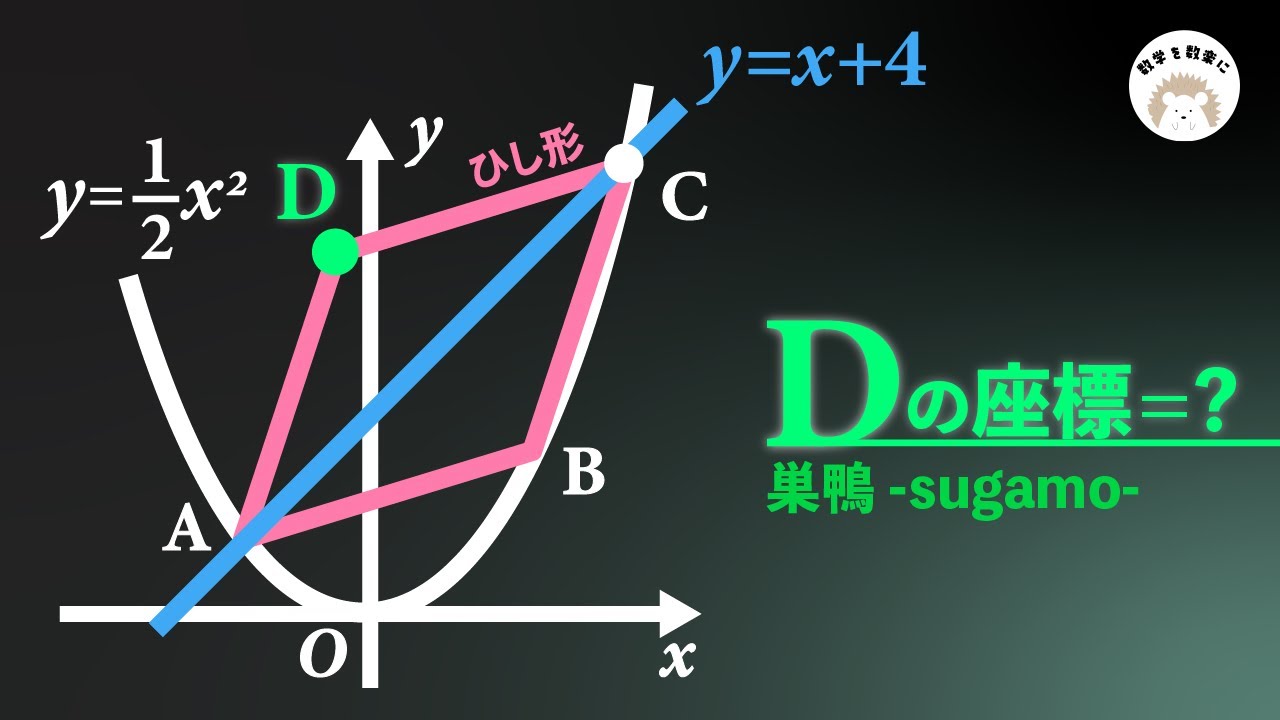
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形
【電撃の方針…！】文字式：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#中央大学杉並高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
(x+2)(y+2)=(x-2)(y-2)のとき、(2x+√5)(2y+√5)+4x^2.の値を求めなさい。
この動画を見る
(x+2)(y+2)=(x-2)(y-2)のとき、(2x+√5)(2y+√5)+4x^2.の値を求めなさい。
【華麗に解答…！】文字式：京都女子高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
a<0,b<0とする。a-b=2,ab=5のとき、a+bの値を求めなさい。
この動画を見る
a<0,b<0とする。a-b=2,ab=5のとき、a+bの値を求めなさい。
【これなら分かる…！】図形：日本大学第三高等学校～全国入試問題解法
単元：
#算数(中学受験)#数学(中学生)#平面図形#平面図形その他#高校入試過去問(数学)#日本大学第三高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
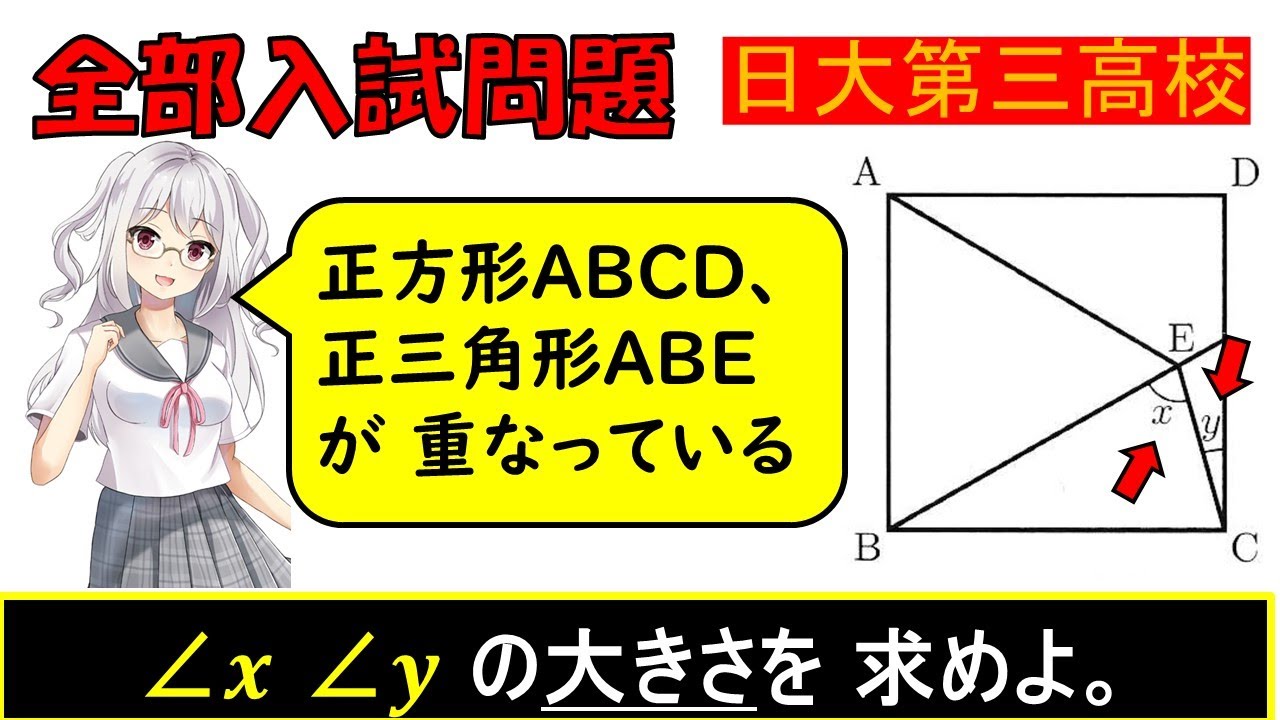
正方形ABCD、正三角形ABEが重なっている。角x,yの大きさを求めよ。
この動画を見る
正方形ABCD、正三角形ABEが重なっている。角x,yの大きさを求めよ。
【ナットクして完答…！】整数：明治大学付属中野高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
3けたの正の整数において、上2けたの数から一の位の数を引いた数が11の倍数のとき、もとの3けたの整数は11の倍数であることを証明せよ。
この動画を見る
3けたの正の整数において、上2けたの数から一の位の数を引いた数が11の倍数のとき、もとの3けたの整数は11の倍数であることを証明せよ。
【一撃で処理…！】図形：長野県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#相似な図形#高校入試過去問(数学)#長野県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
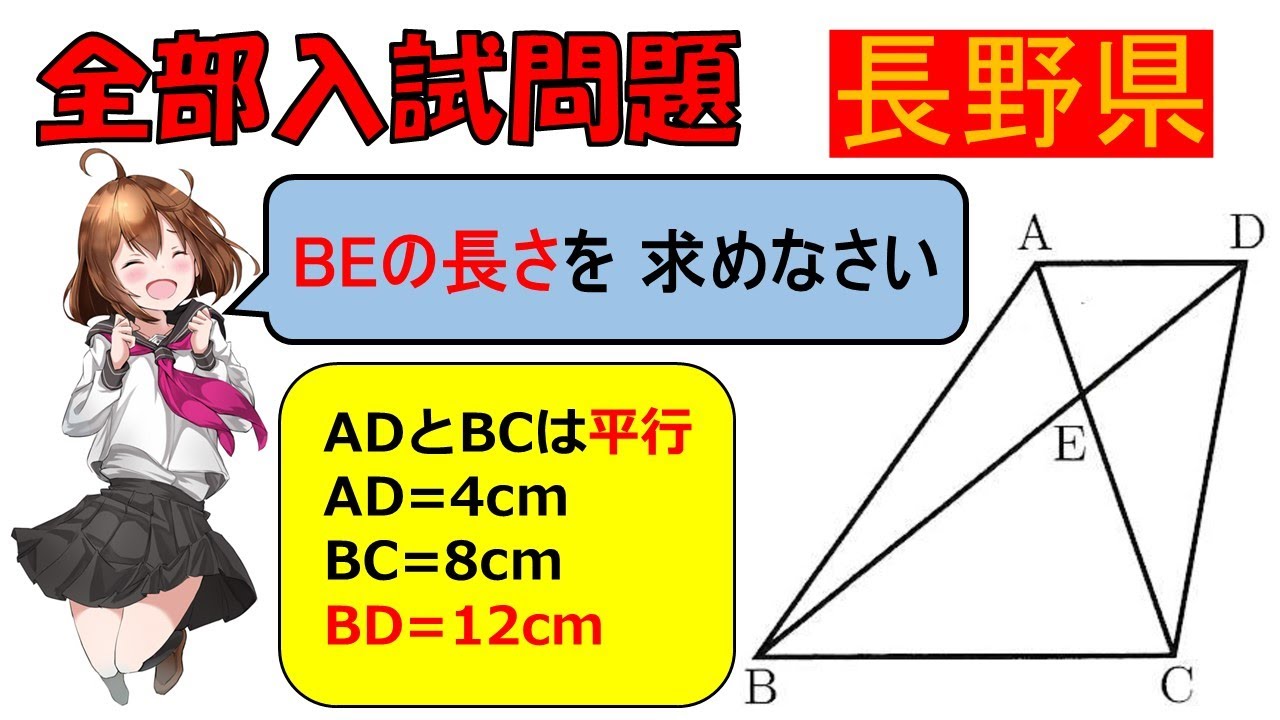
台形ABCDについて(※図は動画内参照)AD=4cm,BC=8cm,BD=12cmのときBEの長さを求めなさい。
この動画を見る
台形ABCDについて(※図は動画内参照)AD=4cm,BC=8cm,BD=12cmのときBEの長さを求めなさい。
【カントウしよう…！】二次方程式：早稲田大学本庄高等学院～全国入試問題解法
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
2次方程式 (√5+√3)x²+2√3x-5√3=0 を解け。
この動画を見る
2次方程式 (√5+√3)x²+2√3x-5√3=0 を解け。
【ダ・ビンチの思考…！】確率：福岡県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#確率#福岡県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
4枚の硬貨A、B、C、Dを同時に投げる。少なくとも1枚は表が出る確率を求めよ。硬貨のそれぞれについて、表と裏の出ることは同様に確からしいとする。
この動画を見る
4枚の硬貨A、B、C、Dを同時に投げる。少なくとも1枚は表が出る確率を求めよ。硬貨のそれぞれについて、表と裏の出ることは同様に確からしいとする。
mathematical formula : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #占い #高校受験 #勉強 #公文式
単元：
#数学(中学生)#高校入試過去問(数学)#ラ・サール高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
x=√7+√2,y=√7-√2のとき、x^4-6x^2y^2+y^4.の値を求めよ。
この動画を見る
x=√7+√2,y=√7-√2のとき、x^4-6x^2y^2+y^4.の値を求めよ。
【すぐに「分かる」…！】図形：百合学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
正八角形の１つの内角の大きさを求めなさい。
この動画を見る
正八角形の１つの内角の大きさを求めなさい。
【公式より思考力…！】整数：大阪偕星学園高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
自然数xに対して、をx以下の素数の和と定める。
たとえば、５以下の素数も６以下の素数も２，３，５であるから
=10,=10.である。
このとき、=41になるxのうち最大のものを求めなさい。
この動画を見る
自然数xに対して、をx以下の素数の和と定める。
たとえば、５以下の素数も６以下の素数も２，３，５であるから
=10,=10.である。
このとき、=41になるxのうち最大のものを求めなさい。
integer problems : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #勉強 #高校受験 #占い #公文式 #恋愛
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
230を自然数nで割るとあまり20となるnの個数を求めよ。
この動画を見る
230を自然数nで割るとあまり20となるnの個数を求めよ。
【いかに攻めるか…！】整数：大谷高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
40-3aが自然数の平方となるような自然数aは全部で何個あるか？
この動画を見る
40-3aが自然数の平方となるような自然数aは全部で何個あるか？
【応用力をつける…！】二次方程式：四天王寺高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#２次方程式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
x^2-6x-5=0の２解の和と積が、x^2+ax+b=0の２解になるとき、定数a,bの値を求めなさい。
この動画を見る
x^2-6x-5=0の２解の和と積が、x^2+ax+b=0の２解になるとき、定数a,bの値を求めなさい。
【ミスのない計算方法…！】文字式：早稲田大阪高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#式の計算（単項式・多項式・式の四則計算）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
(-5xy/6)^3÷(-7x^2y/6)×x^4.を計算しなさい。
この動画を見る
(-5xy/6)^3÷(-7x^2y/6)×x^4.を計算しなさい。
equation : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #占い #高校受験 #勉強 #公文式 #歌ってみた #式の値
単元：
#数学(中学生)#中２数学#連立方程式#高校入試過去問(数学)#西大和学園高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
aを定数とする。x,yについての連立方程式
4y-3x=a
2x-3y=4
の解がx+y=aを満たすとき、定数aの値を求めよ。
この動画を見る
aを定数とする。x,yについての連立方程式
4y-3x=a
2x-3y=4
の解がx+y=aを満たすとき、定数aの値を求めよ。
スマートに軽やかに…！】文字式：文教大学付属高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
x-y=-2
xy=8
のとき
x³y-2x²y²+xy³
の値を計算しなさい。
この動画を見る
x-y=-2
xy=8
のとき
x³y-2x²y²+xy³
の値を計算しなさい。
【手を動かせ…！】因数分解：八雲学園高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の式を展開しなさい
(x+y+z)(x-y-z)
この動画を見る
次の式を展開しなさい
(x+y+z)(x-y-z)
【直感より理解…！】確率：精華女子高等学校～全国入試問題解法
単元：
#数学(中学生)#中２数学#確率#高校入試過去問(数学)#精華女子高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
A、B、C、D、Eの5人から3人の委員を選ぶとき
3人の委員の中にAが含まれる確率を求めなさい
この動画を見る
A、B、C、D、Eの5人から3人の委員を選ぶとき
3人の委員の中にAが含まれる確率を求めなさい
equation : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #高校受験
単元：
#数学(中学生)#中２数学#連立方程式#高校入試過去問(数学)#大阪星光学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
ax-y=4 (a,b,>0)
x+by=7
解をa,bを用いて表せ
この動画を見る
ax-y=4 (a,b,>0)
x+by=7
解をa,bを用いて表せ
【「定石」の前に…！】因数分解：自由が丘学園高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
(a+2b)²-3(a+2b)+2(a+b)-2(1-b)を因数分解しなさい
この動画を見る
(a+2b)²-3(a+2b)+2(a+b)-2(1-b)を因数分解しなさい