 TK数学
TK数学
 TK数学
TK数学
【数学】中高一貫校問題集2幾何158:三平方の定理:線分の長さ

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
この動画を見る
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
【数学】中高一貫校問題集2幾何157:三平方の定理:三角形の面積

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
この動画を見る
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
【数学】中高一貫校問題集2幾何156:直角三角形の3辺の長さの決定

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
この動画を見る
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
【数学】中高一貫校問題集 数学3 数式・関数編 111 実数解が存在することの証明

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
この動画を見る
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
【数学】中高一貫校問題集 数学3 数式・関数編 109 虚数を含む2次方程式の解法
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
この動画を見る
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
【数学】中高一貫校問題集2幾何150:円:2つの円 方べきの定理の利用
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
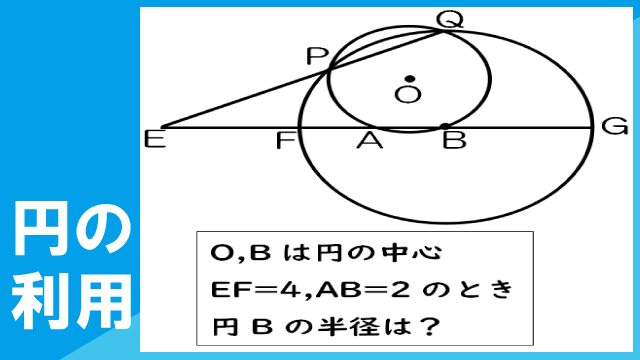
図のように、2つの円O、Bが2点P、Qで交わり、さらに、円Oは円Bの直径FGと2点A、Bで交わっている。点Bは円Bの中心である。また、点Eは2直線PQ、FGの交点である。EF=4、AB=2のとき、円Bの半径を求めなさい。
この動画を見る
図のように、2つの円O、Bが2点P、Qで交わり、さらに、円Oは円Bの直径FGと2点A、Bで交わっている。点Bは円Bの中心である。また、点Eは2直線PQ、FGの交点である。EF=4、AB=2のとき、円Bの半径を求めなさい。
【数学】中高一貫校問題集2幾何149:円:2つの円 接弦定理の利用
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
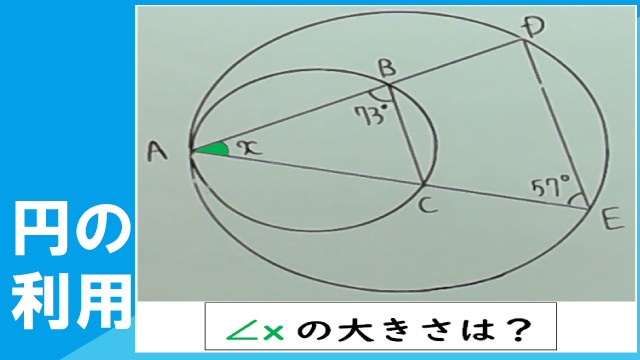
図のように、2つの円は点Aで内接している。このとき、∠xの大きさを求めなさい。
この動画を見る
図のように、2つの円は点Aで内接している。このとき、∠xの大きさを求めなさい。
【数学】中高一貫校問題集2幾何148:円:2つの円 内接四角形と円周角
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
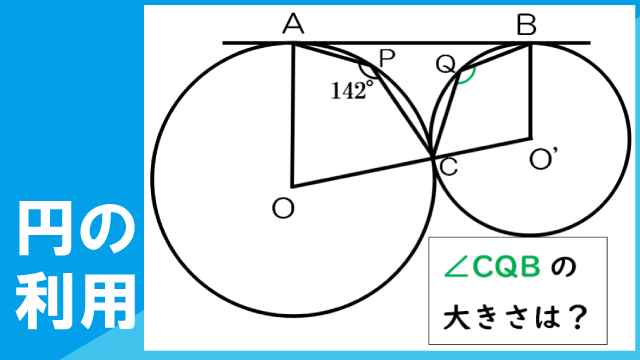
図のように、点O、O'を中心とする2つの円が、直線lにそれぞれ点A、Bで接しており、点Cで円どうしが接している。また、図のように、弧AC上の点をP、弧BC上の点をQとする。∠APC=142°のとき、∠BQCの大きさを求めなさい。
この動画を見る
図のように、点O、O'を中心とする2つの円が、直線lにそれぞれ点A、Bで接しており、点Cで円どうしが接している。また、図のように、弧AC上の点をP、弧BC上の点をQとする。∠APC=142°のとき、∠BQCの大きさを求めなさい。
【数学】中高一貫校問題集2幾何147:円:2つの円:相似の利用
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
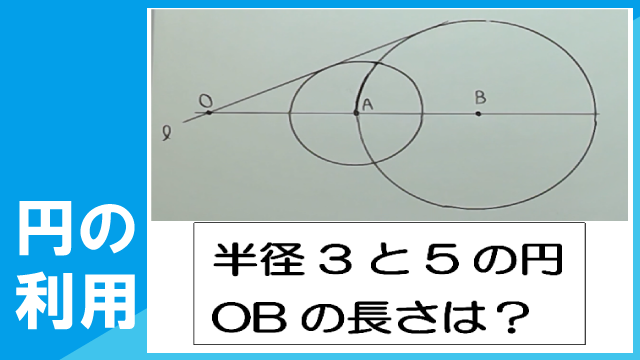
図のように、点A、Bを中心とする円A、Bがあり、半径はそれぞれ3cm、5cmである。また、点Aは円Bの円周上の点であり、直線lは2つの円の共通接線である。直線ABとlの交点をOとするとき、線分OBの長さを求めなさい。
この動画を見る
図のように、点A、Bを中心とする円A、Bがあり、半径はそれぞれ3cm、5cmである。また、点Aは円Bの円周上の点であり、直線lは2つの円の共通接線である。直線ABとlの交点をOとするとき、線分OBの長さを求めなさい。
【数学】中高一貫校問題集2幾何140:円:方べきの定理:√5の作図
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
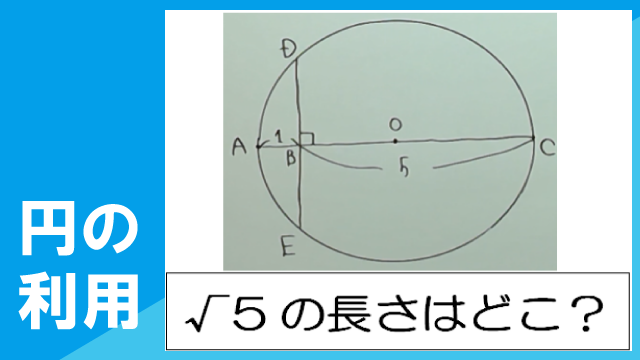
長さ1の線分ABから、長さ√5の線分を次の手順で作図できる。
①線分ABのBを超える延長線上に、BC=5となる点Cをとる。
②線分ACを直径とする円Oをかく。
③Bを通り、直線ABに垂直な直線を引き、点Oとの交点をD、Eとする。
(1)長さが√5の線分を次のうちからすべて答えなさい。
AD,AE,AO,BD,BO,CD,CE,CO,DO,EO
(2)(1)で答えた線分の長さが√5であることを証明しなさい。
この動画を見る
長さ1の線分ABから、長さ√5の線分を次の手順で作図できる。
①線分ABのBを超える延長線上に、BC=5となる点Cをとる。
②線分ACを直径とする円Oをかく。
③Bを通り、直線ABに垂直な直線を引き、点Oとの交点をD、Eとする。
(1)長さが√5の線分を次のうちからすべて答えなさい。
AD,AE,AO,BD,BO,CD,CE,CO,DO,EO
(2)(1)で答えた線分の長さが√5であることを証明しなさい。
【数学】中高一貫校問題集2幾何139:円:方べきの定理:4点が円周上にあることの証明

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、円Oの外部に点Pがあり、Pから円Oに接線PA、PBを引く。また、Pを通り、円Oと2点C、Dで交わる直線を引く。ただし、直線CDは円の中心を通らないものとする。このとき、線分ABの中点をMとすると、4点C、M、O、Dは1つの円周上にあることを証明しなさい。
この動画を見る
図のように、円Oの外部に点Pがあり、Pから円Oに接線PA、PBを引く。また、Pを通り、円Oと2点C、Dで交わる直線を引く。ただし、直線CDは円の中心を通らないものとする。このとき、線分ABの中点をMとすると、4点C、M、O、Dは1つの円周上にあることを証明しなさい。
【数学】中高一貫校問題集2幾何138:円:方べきの定理:円の半径と線分の積
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
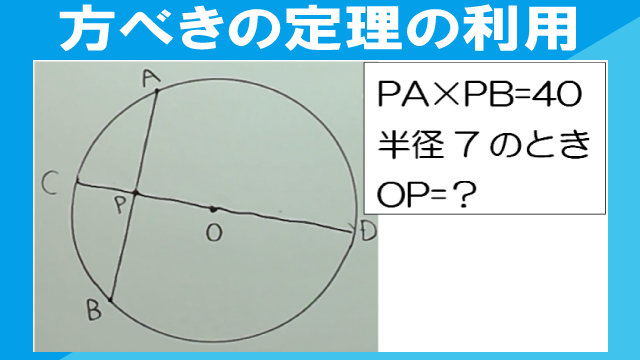
点Oを中心とする半径7の円の内部に点Pがある。Pを通る円Oの弦ABについて、PA×PB=40であるとき、線分OPの長さを求めなさい。
この動画を見る
点Oを中心とする半径7の円の内部に点Pがある。Pを通る円Oの弦ABについて、PA×PB=40であるとき、線分OPの長さを求めなさい。
【数学】中高一貫校問題集2幾何134:円:接弦定理: 4点が同一円周上にあるとき
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
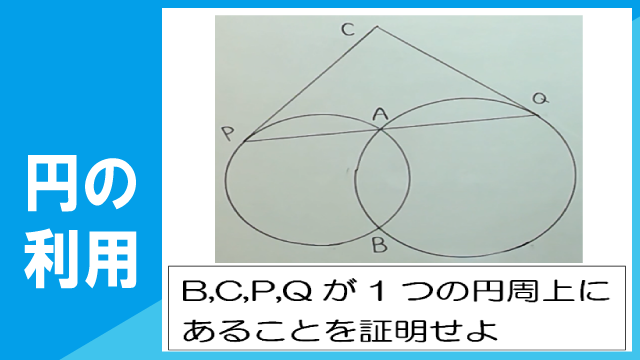
右の図のように、2点A、Bは2円の交点であり、2点P、QはAを通る直線が2円と交わる点である。また、P、Qにおいて、それぞれ円の接線を引き、その交点をCとする。このとき、4点B、C、P、Qは1つの円周上にあることを証明しなさい。
この動画を見る
右の図のように、2点A、Bは2円の交点であり、2点P、QはAを通る直線が2円と交わる点である。また、P、Qにおいて、それぞれ円の接線を引き、その交点をCとする。このとき、4点B、C、P、Qは1つの円周上にあることを証明しなさい。
【数学】中高一貫校問題集2幾何133:円:接弦定理: 相似の証明2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
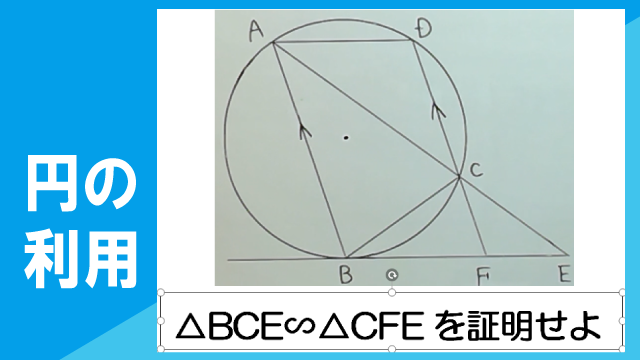
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
この動画を見る
右の図のように、円に内接する二等辺三角形ABCがあり、AB=AC=3cm、BC=2cmである。点Bにおける円の接線と辺ACの延長との交点をEとする。また、Cを通り辺ABに平行な直線が円と交わる点をD、BEと交わる点をFとする。
(1)△BCE∽△CFEであることを証明しなさい。
(2)線分CF、EFの長さをそれぞれ求めなさい。
【数学】中高一貫校問題集2幾何132:円:接弦定理: 相似の証明1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
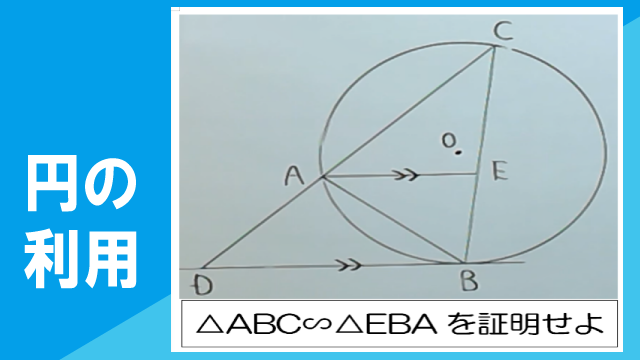
右の図において、△ABCは円Oに内接し、辺BCは辺ABよりも長い。点Bにおける円Oの接線と辺CAの延長との交点をDとし、辺BC上に点Eを、AE//DBとなるようにとる。このとき△ABC∽△EBAであることを証明しなさい。
この動画を見る
右の図において、△ABCは円Oに内接し、辺BCは辺ABよりも長い。点Bにおける円Oの接線と辺CAの延長との交点をDとし、辺BC上に点Eを、AE//DBとなるようにとる。このとき△ABC∽△EBAであることを証明しなさい。
【数学】中高一貫校問題集2幾何131:円:接弦定理:二等辺三角形の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
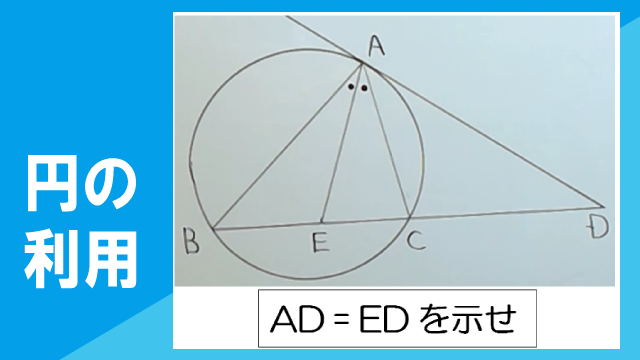
右の図のように、△ABCとその外接円があり、点Aにおける外接円の接線が辺BCの延長と交わる点をDとする。また、∠BACの二等分線がBCと交わる点をEとする。このとき、AD=EDであることを証明しなさい。
この動画を見る
右の図のように、△ABCとその外接円があり、点Aにおける外接円の接線が辺BCの延長と交わる点をDとする。また、∠BACの二等分線がBCと交わる点をEとする。このとき、AD=EDであることを証明しなさい。
【数学】中高一貫校問題集2幾何130:円:接弦定理
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
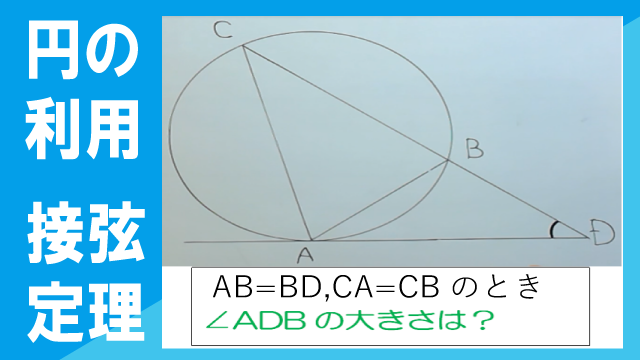
右の図において、ADは円の接線で、AB=BD、CA=CBである。このとき、∠ADBの大きさを求めなさい。
この動画を見る
右の図において、ADは円の接線で、AB=BD、CA=CBである。このとき、∠ADBの大きさを求めなさい。
【数学】中高一貫校問題集2幾何129:円:接弦定理:弧の比と円周角の比
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
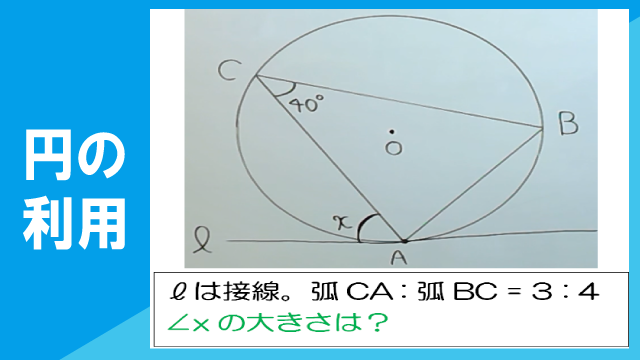
右の図において、直線?は点Aで円Oに接していて、∠ACB=40°である。また、弧AC:弧CB=3:4である。このとき、∠xの大きさを求めなさい。
この動画を見る
右の図において、直線?は点Aで円Oに接していて、∠ACB=40°である。また、弧AC:弧CB=3:4である。このとき、∠xの大きさを求めなさい。
【数学】中高一貫校問題集2幾何124:円:円の接線:外心、内心、重心はどれ?
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
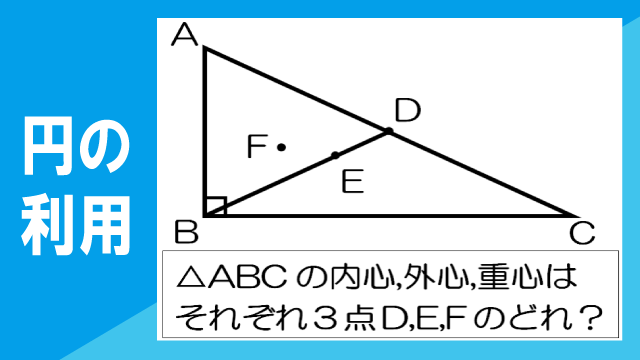
図の△ABCは、∠B=90°の直角三角形であり、3点D、E、Fは△ABCの外心、内心、重心のいずれかである。このとき、△ABCの外心、内心、重心はそれぞれ3点D、E、Fのいずれかであるか答えなさい。
この動画を見る
図の△ABCは、∠B=90°の直角三角形であり、3点D、E、Fは△ABCの外心、内心、重心のいずれかである。このとき、△ABCの外心、内心、重心はそれぞれ3点D、E、Fのいずれかであるか答えなさい。
【数学】中高一貫校問題集2幾何122:円:円の接線:内接円の性質
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
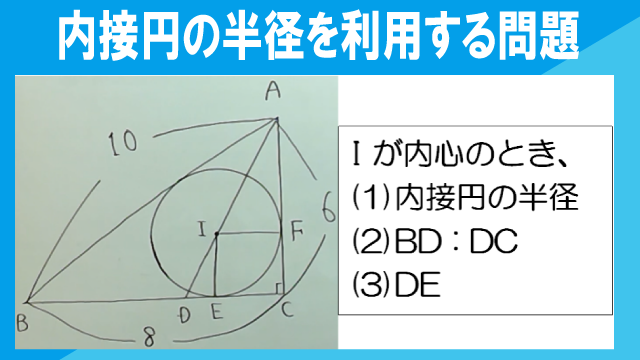
図の△ABCは、∠C=90°の直角三角形である。AB=10cm、BC=8cm、CA=6cmとし、△ABCの内接円の中心をIとする。また、直線AIと辺BCの交点をD、円ⅠとBC、CAの接点をそれぞれE、Fとする。
(1)円Iの半径を求めなさい。
(2)BD:DCを求めなさい。
(3)線分DEの長さを求めなさい。
この動画を見る
図の△ABCは、∠C=90°の直角三角形である。AB=10cm、BC=8cm、CA=6cmとし、△ABCの内接円の中心をIとする。また、直線AIと辺BCの交点をD、円ⅠとBC、CAの接点をそれぞれE、Fとする。
(1)円Iの半径を求めなさい。
(2)BD:DCを求めなさい。
(3)線分DEの長さを求めなさい。
【数学】中高一貫校問題集2幾何121:円:円の接線:三角形の面積と内接円の半径
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
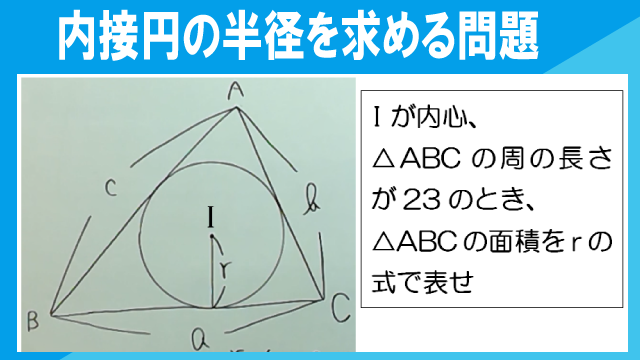
△ABCの周の長さが23、△ABCの内接円の半径がrのとき、△ABCの面積をrを用いて表しなさい。
この動画を見る
△ABCの周の長さが23、△ABCの内接円の半径がrのとき、△ABCの面積をrを用いて表しなさい。
【数学】中高一貫校問題集2幾何120:円:円の接線:内心の性質
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
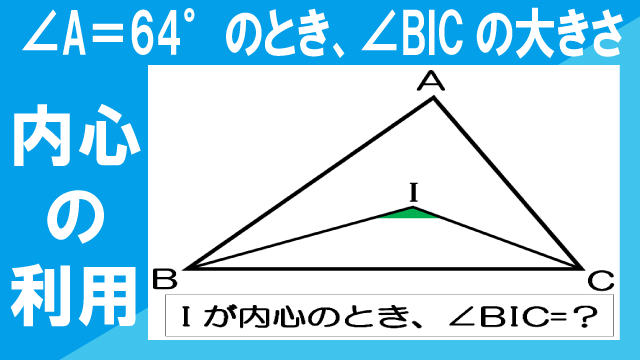
△ABCの内心をIとする。∠A=64°のとき、∠BICの大きさを求めなさい。
この動画を見る
△ABCの内心をIとする。∠A=64°のとき、∠BICの大きさを求めなさい。
【数学】中高一貫校問題集2幾何119:円:円の接線:円外から引いた接線の長さは同じ
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
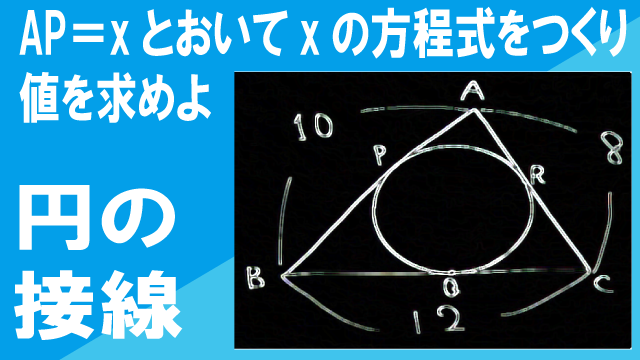
図のように、△ABCの内接円が、辺AB、BC、CA、と接する点を、それぞれP、Q、Rとする。また、AB=10、BC=12、CA=8とする。AP=xとおいてxの方程式をつくり、それを解いてxの値を求めなさい。
この動画を見る
図のように、△ABCの内接円が、辺AB、BC、CA、と接する点を、それぞれP、Q、Rとする。また、AB=10、BC=12、CA=8とする。AP=xとおいてxの方程式をつくり、それを解いてxの値を求めなさい。
【数学】中高一貫校問題集2幾何118:円:円の接線:弧の比=中心角 or 円周角
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
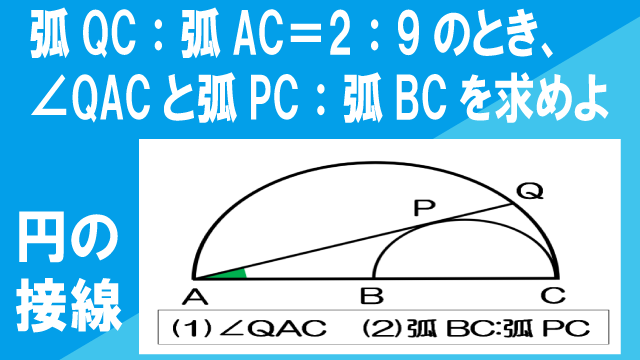
右の図のように、AC、BCを直径とする2つの半径において、大きい半円弦AQは小さい半円に点Pで接している。弧QC:弧AC=2:9のとき、次の問いに答えなさい。
(1)∠QACの大きさを求めなさい。
(2)弧PC:弧BCを求めなさい。
この動画を見る
右の図のように、AC、BCを直径とする2つの半径において、大きい半円弦AQは小さい半円に点Pで接している。弧QC:弧AC=2:9のとき、次の問いに答えなさい。
(1)∠QACの大きさを求めなさい。
(2)弧PC:弧BCを求めなさい。
【数学】中高一貫校問題集2幾何113:円:内接四角形:四角形が内接することの証明2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
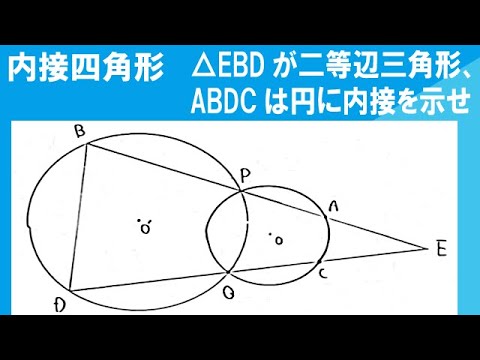
図のように、交わる2つの円O、O'の交点をP、Qとする。また、Pを通る直線と円O、O'の交点をそれぞれA、Bとし、Qを通る直線と円O、O'との交点をそれぞれC、Dとする。△EBDが二等辺三角形のとき、四角形ABDCは円に内接することを証明しなさい。
この動画を見る
図のように、交わる2つの円O、O'の交点をP、Qとする。また、Pを通る直線と円O、O'の交点をそれぞれA、Bとし、Qを通る直線と円O、O'との交点をそれぞれC、Dとする。△EBDが二等辺三角形のとき、四角形ABDCは円に内接することを証明しなさい。
【数学】中高一貫校問題集2幾何112:円:内接四角形:四角形が内接することの証明1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
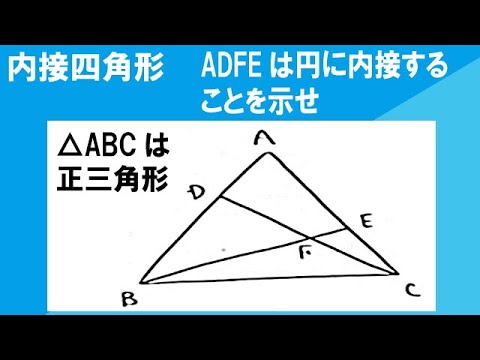
図のように、正三角形ABCの辺AB、CA上にAD=CEとなる点E、Fをそれぞれとる。BE、CDの交点をFとするとき、四角形ADFEは円に内接することを証明しなさい。
この動画を見る
図のように、正三角形ABCの辺AB、CA上にAD=CEとなる点E、Fをそれぞれとる。BE、CDの交点をFとするとき、四角形ADFEは円に内接することを証明しなさい。
【数学】中高一貫校問題集2幾何111:円:内接四角形:一直線上の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
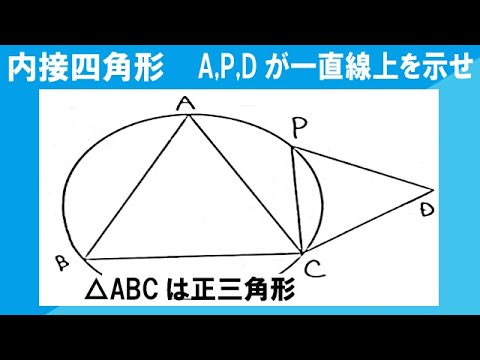
正三角形ABCとその外接円がある。図のように、弧CA上に点Pをとり、正三角形PCDをつくる。このとき、3点A、P、Dは一直線上にあることを証明しなさい。
この動画を見る
正三角形ABCとその外接円がある。図のように、弧CA上に点Pをとり、正三角形PCDをつくる。このとき、3点A、P、Dは一直線上にあることを証明しなさい。
【数学】中高一貫校問題集2幾何110:円:内接四角形:相似の証明
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
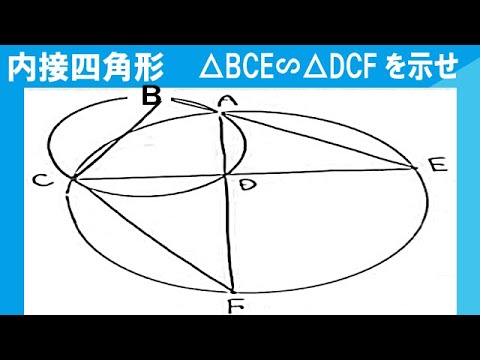
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
この動画を見る
図のように、円に内接する四角形ABCDがある。辺BAとCDをそれぞれ延長した直線の交点をEとし、3点A、C、Eを通る円と辺ADを延長した直線の交点をFとする。このとき、△BCE∽△DCFであることを証明しなさい。
【数学】中高一貫校問題集2幾何109:円:内接四角形:角度の応用2
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
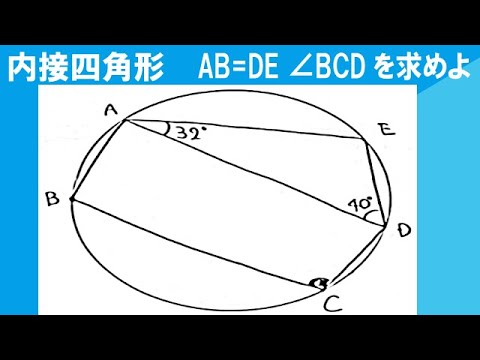
図のように、円に内接する五角形ABCDEがある。AB=DE、∠DAE=32°、∠ADE=40°のとき、∠BCDの大きさを求めなさい。
この動画を見る
図のように、円に内接する五角形ABCDEがある。AB=DE、∠DAE=32°、∠ADE=40°のとき、∠BCDの大きさを求めなさい。
【数学】中高一貫校問題集2幾何108:円:内接四角形:角度の応用1
単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
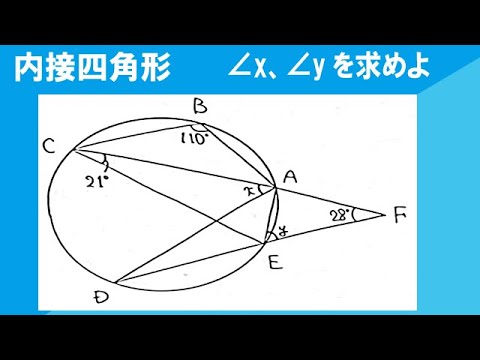
図において、∠x、∠yの大きさを求めなさい。
この動画を見る
図において、∠x、∠yの大きさを求めなさい。
