図形の性質
図形の性質
【数A】図形の性質：チェバの定理とメネラウスの定理ってこういうことだったの？ ただの暗記だと思ってたけど全然違った・・・
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#サクシード#サクシード数学Ⅰ・A#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
チェバメネラウスの定理の解説動画です。
この動画を見る
チェバメネラウスの定理の解説動画です。
東大留年女子もっちゃんとオイラーの公式を学ぶ！最終章
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
オイラーの公式に関して解説していきます.
$e=\displaystyle \lim_{ n \to \infty }(1+\displaystyle \frac{1}{n})^n$
$e^{i \pi}=-1$
この動画を見る
オイラーの公式に関して解説していきます.
$e=\displaystyle \lim_{ n \to \infty }(1+\displaystyle \frac{1}{n})^n$
$e^{i \pi}=-1$
もっちゃんとオイラーの公式を学ぶ 数学の魔術師も出演
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
オイラーの公式に関して解説していきます.
$e^{i \pi}=-1$
この動画を見る
オイラーの公式に関して解説していきます.
$e^{i \pi}=-1$
名古屋市立（医）放物線と円 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x^2$上の点$(a,a^2)$を中心とし、この放射線に接するような円が存在するための$a$の条件は？
出典：名古屋市立大学 過去問
この動画を見る
$y=x^2$上の点$(a,a^2)$を中心とし、この放射線に接するような円が存在するための$a$の条件は？
出典：名古屋市立大学 過去問
北海道大 双曲線と円の共有点 高校数学 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
この動画を見る
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
オイラーの多面体定理 説明（英語）
慶応義塾 正奇数角形にできる鈍角三角形の数 Mathematics Japanese university entrance exam Keio University
単元：
#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2007年 慶應義塾大学
$(1)$正九角形の頂点を結んでできる$84$個の三角形のうち、
純角三角形は何個か。
$(2)$正$2n+1$角形の頂点を結んでできる純角三角形の個数。
この動画を見る
2007年 慶應義塾大学
$(1)$正九角形の頂点を結んでできる$84$個の三角形のうち、
純角三角形は何個か。
$(2)$正$2n+1$角形の頂点を結んでできる純角三角形の個数。
【高校数学】方べきの定理を２秒で証明できるようになろう
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
【高校数学】方べきの定理の証明について解説動画です
この動画を見る
【高校数学】方べきの定理の証明について解説動画です
津田塾大 格子点 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
p,qは互いに素な自然数
(1)A(p,0),B(0,q)
線分AB上には、A,B以外には格子点がないことを示せ
(2)△OABの内部(周上は含まない)の格子点の個数
＊図は動画内参照
この動画を見る
p,qは互いに素な自然数
(1)A(p,0),B(0,q)
線分AB上には、A,B以外には格子点がないことを示せ
(2)△OABの内部(周上は含まない)の格子点の個数
＊図は動画内参照
福田の一夜漬け数学〜図形と方程式〜軌跡(5)動点が２個ある場合の軌跡、高校2年生
単元：
#数A#数Ⅱ#図形の性質#内心・外心・重心とチェバ・メネラウス#図形と方程式#点と直線#円と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 定点$A(2,0),B(4,0)$と円$C:x^2+y^2=9$ がある。
動点$P$が円$C$上を動くとき、$\triangle ABP$の重心$G$の軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 定点$A(2,0),B(4,0)$と円$C:x^2+y^2=9$ がある。
動点$P$が円$C$上を動くとき、$\triangle ABP$の重心$G$の軌跡を求めよ。
福田の一夜漬け数学〜図形と方程式〜円の方程式(2)三角形の外心、高校2年生
単元：
#数A#数Ⅱ#図形の性質#内心・外心・重心とチェバ・メネラウス#図形と方程式#円と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 3点$A(-2,6),B(1,-3),C(5,-1)$を頂点とする$\triangle ABC$の外心の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 3点$A(-2,6),B(1,-3),C(5,-1)$を頂点とする$\triangle ABC$の外心の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜直線の方程式(9)点と直線の距離の公式と三角形の内心、高校2年生
単元：
#数A#数Ⅱ#図形の性質#内心・外心・重心とチェバ・メネラウス#図形と方程式#点と直線#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 3直線$\ell:3x+4y-36=0,$ $m:4x-3y+27=0,$ $n:3x-4y-20=0$で
囲まれた三角形の内心の座標を求めよ。
この動画を見る
${\Large\boxed{1}}$ 3直線$\ell:3x+4y-36=0,$ $m:4x-3y+27=0,$ $n:3x-4y-20=0$で
囲まれた三角形の内心の座標を求めよ。
福田の一夜漬け数学〜図形と方程式〜内分・外分公式、高校2年生
単元：
#数A#数Ⅱ#図形の性質#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#図形と方程式#点と直線#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 3点$A(-1,1),B(1,-2),C(5,0)$がある。次の点の座標を求めよ。
(1)線分ABを2:1に内分する点。
(2)線分CAを2:1に外分する点。
(3)線分BCの中点。
(4)$\triangle$ ABCの重心。
(5)4点A,B,C,Dが平行四辺形の4つの頂点になるような点D。
この動画を見る
${\Large\boxed{1}}$ 3点$A(-1,1),B(1,-2),C(5,0)$がある。次の点の座標を求めよ。
(1)線分ABを2:1に内分する点。
(2)線分CAを2:1に外分する点。
(3)線分BCの中点。
(4)$\triangle$ ABCの重心。
(5)4点A,B,C,Dが平行四辺形の4つの頂点になるような点D。
福田の一夜漬け数学〜図形と方程式〜２点間の距離の公式(2)高校2年生
単元：
#数Ⅱ#図形の性質#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#図形と方程式#点と直線#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
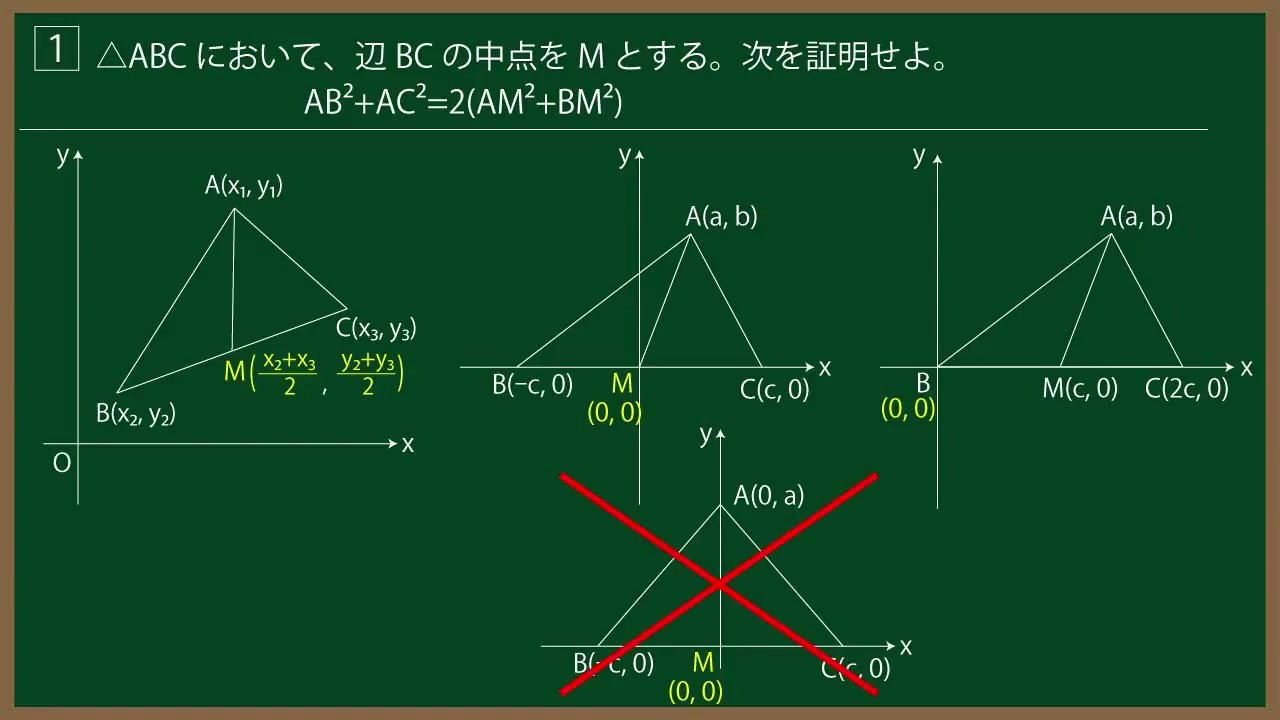
${\Large\boxed{1}}$ $\triangle ABC$において、辺$BC$の中点を$M$とする。次を証明せよ。
$AB^2+AC^2=2(AM^2+BM^2)$
${\Large\boxed{2}}$ $\triangle ABC$の重心をGとするとき、次を証明せよ。
$AB^2+AC^2=BG^2+$$CG^2+$$4AG^2$
(注意)$A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$のとき$\triangle ABC$の重心の座標は
$\left(\displaystyle \frac{x_1+x_2+x_3}{3},\displaystyle \frac{y_1+y_2+y_3}{3}\right)$
この動画を見る
${\Large\boxed{1}}$ $\triangle ABC$において、辺$BC$の中点を$M$とする。次を証明せよ。
$AB^2+AC^2=2(AM^2+BM^2)$
${\Large\boxed{2}}$ $\triangle ABC$の重心をGとするとき、次を証明せよ。
$AB^2+AC^2=BG^2+$$CG^2+$$4AG^2$
(注意)$A(x_1,y_1),B(x_2,y_2),C(x_3,y_3)$のとき$\triangle ABC$の重心の座標は
$\left(\displaystyle \frac{x_1+x_2+x_3}{3},\displaystyle \frac{y_1+y_2+y_3}{3}\right)$
名古屋大 円の方程式 ２円と直線に接する円 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比（三角比・拡張・相互関係・単位円）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)#名古屋大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'08名古屋大学過去問題
2つの円、$x^2+(y-2)^2=9$と$(x-4)^2+(y+4)^2=1$に外接し、x=6と接する円を求めよ。
この動画を見る
'08名古屋大学過去問題
2つの円、$x^2+(y-2)^2=9$と$(x-4)^2+(y+4)^2=1$に外接し、x=6と接する円を求めよ。
【受験対策】数学－図形８
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
この動画を見る
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
【補足動画】受験対策・図形７の補足
単元：
#数Ⅰ#数A#図形の性質#図形と計量#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
【補足動画】受験対策・図形７の補足します.
この動画を見る
【補足動画】受験対策・図形７の補足します.
【受験対策】数学－図形７
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1のような正五角柱において,
辺$AB$とねじれの位置にある辺の数を求めよう.
②右の図2で,印のあるすべての角の大きさの合計を求めなさい.
③右の図3で,平行四辺形$ABCD$と平行四辺形$DEFG$は合同で,
3つの頂点$A,D,G$は1直線上にある.
$BF$と辺$AD$,辺$DE$との交点をそれぞれ$H,I$とする.
$\triangle ABH$の面積が$18cm^2$,$\triangle DHI$の面積が
$4cm^2$のとき,$\triangle EFI$の面積を求めなさい.
図は動画内参照
この動画を見る
①右の図1のような正五角柱において,
辺$AB$とねじれの位置にある辺の数を求めよう.
②右の図2で,印のあるすべての角の大きさの合計を求めなさい.
③右の図3で,平行四辺形$ABCD$と平行四辺形$DEFG$は合同で,
3つの頂点$A,D,G$は1直線上にある.
$BF$と辺$AD$,辺$DE$との交点をそれぞれ$H,I$とする.
$\triangle ABH$の面積が$18cm^2$,$\triangle DHI$の面積が
$4cm^2$のとき,$\triangle EFI$の面積を求めなさい.
図は動画内参照
【高校数学】 数A－６４ 直線と平面③
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
正六面体の各面の対角線の交点を頂点とし,
隣り合う面どうしの頂点を結ぶことによって,
正六面体の中に正八面体ができる.
このとき、,次の場合について,正八面体の体積を求めよう.
①正六面体の1辺の長さが6
②正八面体の1辺の長さが6
図は動画内参照
この動画を見る
正六面体の各面の対角線の交点を頂点とし,
隣り合う面どうしの頂点を結ぶことによって,
正六面体の中に正八面体ができる.
このとき、,次の場合について,正八面体の体積を求めよう.
①正六面体の1辺の長さが6
②正八面体の1辺の長さが6
図は動画内参照
【高校数学】 数A－６３ 直線と平面②
単元：
#数A#図形の性質#空間における垂直と平行と多面体（オイラーの法則）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
凸多面体の①の数をV,②の数をe,③の数を$f$とすると,
$v-e+f=2$が成り立つ.これを④定理という.
空間内の直線$l,m,n$や,平面$P,Q,R$について,
次の記述が正しいときは○,正しくないときは×で答えよう.
⑤$\ell \perp P,m\perp P$のとき,$\ell \perp m$である.
⑥$\ell /\!/ P,m/\!/ P$のとき,$\ell /\!/m$である.
⑦$P /\!/ \ell,Q /\!/ \ell$のとき,$P/\!/ Q$である.
⑧$P\perp Q,Q /\!/ R$のとき,$P\perp R$である.
⑨$\ell \perp m,m\perp n$のとき,$\ell /\!/ n$である.
この動画を見る
凸多面体の①の数をV,②の数をe,③の数を$f$とすると,
$v-e+f=2$が成り立つ.これを④定理という.
空間内の直線$l,m,n$や,平面$P,Q,R$について,
次の記述が正しいときは○,正しくないときは×で答えよう.
⑤$\ell \perp P,m\perp P$のとき,$\ell \perp m$である.
⑥$\ell /\!/ P,m/\!/ P$のとき,$\ell /\!/m$である.
⑦$P /\!/ \ell,Q /\!/ \ell$のとき,$P/\!/ Q$である.
⑧$P\perp Q,Q /\!/ R$のとき,$P\perp R$である.
⑨$\ell \perp m,m\perp n$のとき,$\ell /\!/ n$である.
【高校数学】 数A－６２ 直線と平面①
単元：
#数A#図形の性質#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問題1
右の図の立方体において,次の2直線のなす角$\theta$を
求めよう.ただし,$0°\leqq \theta\leqq 90°$とする.
①$AB$と$CH$
②$AC$と$DG$
問題2
右の図は直方体から三角柱を切り取った立体である.
③直線$AB$と平行な直線をすべて求めよう.
④直線$AE$とねじれの位置にある直線をすべて求めよう.
図は動画内参照
この動画を見る
問題1
右の図の立方体において,次の2直線のなす角$\theta$を
求めよう.ただし,$0°\leqq \theta\leqq 90°$とする.
①$AB$と$CH$
②$AC$と$DG$
問題2
右の図は直方体から三角柱を切り取った立体である.
③直線$AB$と平行な直線をすべて求めよう.
④直線$AE$とねじれの位置にある直線をすべて求めよう.
図は動画内参照
【高校数学】 数A－６１ 作図⑤
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①1辺の長さを1とする正五角形の対角線の長さを求めよう.
②線分$AB$を1辺とする正五角形を作図しよう.
この動画を見る
①1辺の長さを1とする正五角形の対角線の長さを求めよう.
②線分$AB$を1辺とする正五角形を作図しよう.
【高校数学】 数A－６０ 作図④
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①円$O$の外部の点$P$から円$O$に引いた接線を作図しよう.
②線分$AB$を直径とする半円に内接する
正方形$CDEF$を作図しよう.
図は動画内参照
この動画を見る
①円$O$の外部の点$P$から円$O$に引いた接線を作図しよう.
②線分$AB$を直径とする半円に内接する
正方形$CDEF$を作図しよう.
図は動画内参照
【高校数学】 数A－５９ 作図③
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
長さ1の線分$AB$と,長さ$a,b$の2つの線分が与えられたとき,
次の線分を作図しよう.
①長さ$a,b$の線分
②長さ$\dfrac{a}{b}$の線分
③長さ$a^2$の線分
④長さ1の線分$AB$が与えられたとき,
長さ$\sqrt3$の線分を作図しよう.
図は動画内参照
この動画を見る
長さ1の線分$AB$と,長さ$a,b$の2つの線分が与えられたとき,
次の線分を作図しよう.
①長さ$a,b$の線分
②長さ$\dfrac{a}{b}$の線分
③長さ$a^2$の線分
④長さ1の線分$AB$が与えられたとき,
長さ$\sqrt3$の線分を作図しよう.
図は動画内参照
【高校数学】 数A－５８ 作図②
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
与えられた線分$AB$に対して,次の点を作図しよう.
①線分$AB$を$1:3$に内分する点$P$
②線分$AB$を$1:3$に外分する点$Q$
図は動画内参照
この動画を見る
与えられた線分$AB$に対して,次の点を作図しよう.
①線分$AB$を$1:3$に内分する点$P$
②線分$AB$を$1:3$に外分する点$Q$
図は動画内参照
【高校数学】 数A－５７ 作図①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の内接円を作図しよう.
②線分$AB$を斜辺とし,他の1辺の長さが$\dfrac{1}{2}AB$である
直角三角形を作図しよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の内接円を作図しよう.
②線分$AB$を斜辺とし,他の1辺の長さが$\dfrac{1}{2}AB$である
直角三角形を作図しよう.
図は動画内参照
【高校数学】 数A－５６ ２つの円の位置関係と共通接線③
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①2つの円がTで内接している.
内側の円の接線が外側の円と交わる点を$A,B$とし,その接点を$P$とする.
このとき,$TP$は$\angle ATB$を2等分することを証明しよう.
図は動画内参照
この動画を見る
①2つの円がTで内接している.
内側の円の接線が外側の円と交わる点を$A,B$とし,その接点を$P$とする.
このとき,$TP$は$\angle ATB$を2等分することを証明しよう.
図は動画内参照
【高校数学】 数A－５５ ２つの円の位置関係と共通接線②
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図で,直線$AB$は円$O,O'$に,それぞれ点$A,B$で接している.
線分$AB$の長さを求めよう.
①円$O,O'$の半径が,それぞれ5,4
中心間の距離が6
②円$O,O'$の半径がそれぞれ6,3
中心間の距離が13
図は動画内参照
この動画を見る
下の図で,直線$AB$は円$O,O'$に,それぞれ点$A,B$で接している.
線分$AB$の長さを求めよう.
①円$O,O'$の半径が,それぞれ5,4
中心間の距離が6
②円$O,O'$の半径がそれぞれ6,3
中心間の距離が13
図は動画内参照
【高校数学】 数A－５４ ２つの円の位置関係と共通接線①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問題1
それぞれの半径が$r,r'(r\gt r')$である2つの円の中心間の距離を$d$とするとき,
①~⑤における$r,r',d$の関係をかこう.
①互いに外部にある
②外接する
③ 2点で交わる
④内接する
⑤一方が他方を含む
問題2
半径が12と5の2つの円の中心間の距離が次のような場合,
2つの円の位置関係と共通接線の数をかこう.
⑥17
⑦6
⑧11
この動画を見る
問題1
それぞれの半径が$r,r'(r\gt r')$である2つの円の中心間の距離を$d$とするとき,
①~⑤における$r,r',d$の関係をかこう.
①互いに外部にある
②外接する
③ 2点で交わる
④内接する
⑤一方が他方を含む
問題2
半径が12と5の2つの円の中心間の距離が次のような場合,
2つの円の位置関係と共通接線の数をかこう.
⑥17
⑦6
⑧11
【高校数学】 数A－５３ 方べきの定理③
単元：
#数A#図形の性質#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①2つの円が点$A$で同じ直線に接している.
この直線上の$A$と異なる点$B$を通る2本の直線と,
2円との2つの交点をそれぞれ$C,D$および$E,F$とする.
このとき,4点$C,D,E,F$は同一円周上にあることを証明しよう.
図は動画内参照
この動画を見る
①2つの円が点$A$で同じ直線に接している.
この直線上の$A$と異なる点$B$を通る2本の直線と,
2円との2つの交点をそれぞれ$C,D$および$E,F$とする.
このとき,4点$C,D,E,F$は同一円周上にあることを証明しよう.
図は動画内参照