 整数の性質
整数の性質
 整数の性質
整数の性質
大学入試問題#518「2024年の整数問題はこれで決まり!!」 英語orドイツ語 #整数問題
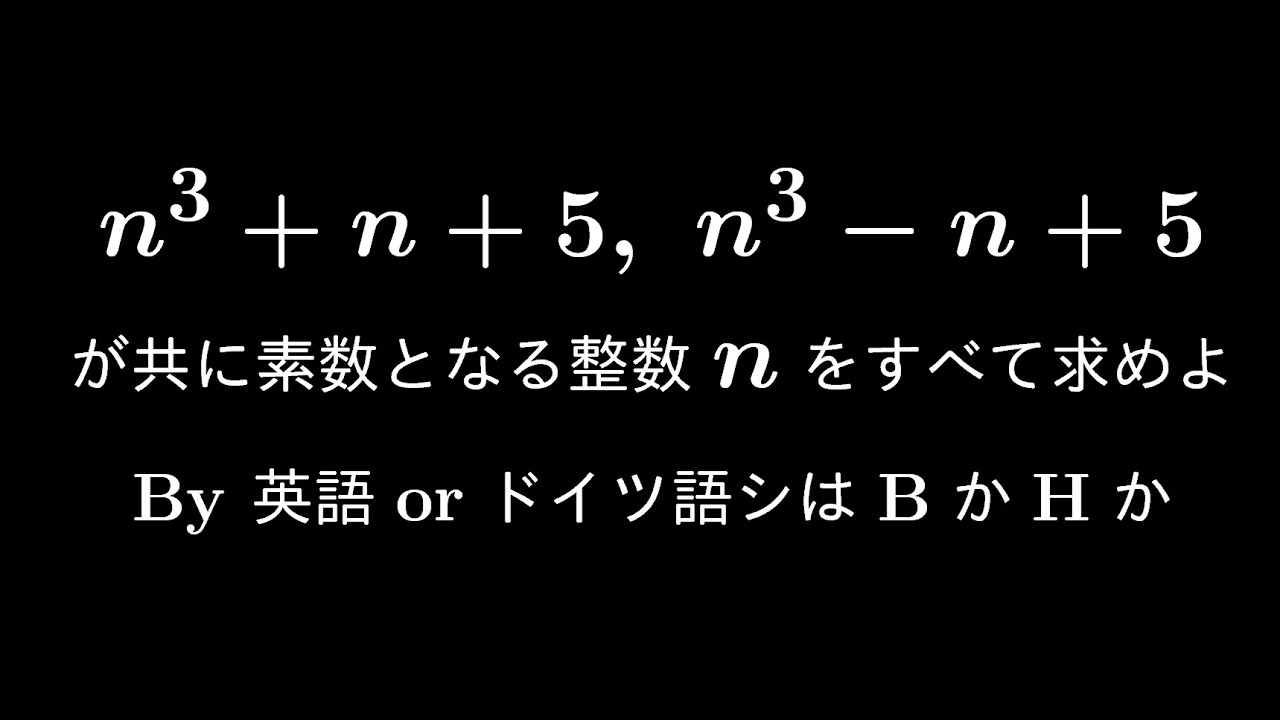
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n^3+n+5$
$n^3-n+5$
が共に素数となるような整数$n$を求めよ
この動画を見る
$n^3+n+5$
$n^3-n+5$
が共に素数となるような整数$n$を求めよ
千葉大 整数解を持つ条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
この動画を見る
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
大学入試問題#517「どこでも解説されてる良問」 京都大学(2018) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n^3-yn+9$が素数となるような整数$n$をすべて求めよ。
出典:2018年京都大学 入試問題
この動画を見る
$n^3-yn+9$が素数となるような整数$n$をすべて求めよ。
出典:2018年京都大学 入試問題
【ガチ良問】素数が絡んだ整数問題の難問です【数学】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
この動画を見る
pを素数,kを自然数とする。
$12p^{2}+12p+1=k^{2}$を満たすようなpの値を求めよ。
千葉大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは奇数の素数である.
$N=(P+1)(P+3)(P+5)$
(1)Nは48の倍数であることを示せ.
(2)Nが144の倍数となるPを小さい順に5つ答えよ.
千葉大過去問
この動画を見る
Pは奇数の素数である.
$N=(P+1)(P+3)(P+5)$
(1)Nは48の倍数であることを示せ.
(2)Nが144の倍数となるPを小さい順に5つ答えよ.
千葉大過去問
福田の数学〜早稲田大学2023年理工学部第1問〜整式の割り算の商に関する論証

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数列#漸化式#数学的帰納法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{1}$ nを自然数として、整式$(3x+2)^n$を$x^2$+$x$+1で割った余りを$a_nx$+$b_n$とおく。
(1)$a_{n+1}$と$b_{n+1}$を、それぞれ$a_n$と$b_n$を用いて表せ。
(2)全てのnに対して、$a_n$と$b_n$は7で割り切れないことを示せ。
(3)$a_n$と$b_n$を$a_{n+1}$と$b_{n+1}$で表し、全てのnに対して、2つの整数$a_n$と$b_n$は互いに素であることを示せ。
2023早稲田大学理工学部過去問
割って余る問題だけど。。。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
6で割ると3余り、8で割ると5余る3ケタの自然数のうち最小のものを求めよ。
高知学芸高等学校
この動画を見る
6で割ると3余り、8で割ると5余る3ケタの自然数のうち最小のものを求めよ。
高知学芸高等学校
ただの因数分解と整数問題

単元:
#数Ⅰ#数A#数と式#場合の数と確率#式の計算(整式・展開・因数分解)#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
この動画を見る
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
よく間違える問題。整数部分と小数部分。計算が面白いんだ 東邦大附属東邦

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$5- \sqrt 7$の整数部分をa、小数部分をbとするとき
$b^2(a-b+4)=?$
東邦大学付属東邦高等学校
この動画を見る
$5- \sqrt 7$の整数部分をa、小数部分をbとするとき
$b^2(a-b+4)=?$
東邦大学付属東邦高等学校
福田の数学〜慶應義塾大学2023年薬学部第1問(7)〜n進法と割り算の余り

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (7)整数Zはn進法で表すとk+1桁であり、$n^k$の位の数が4、$n^i$ (1≦i≦k-1)の位の数が0、$n^0$の位の数が1となる。ただし、nはn≧3を満たす整数、kはk≧2を満たす整数とする。
(i)k=3とする。Zをn+1で割った時の余りは$\boxed{\ \ テ\ \ }$である。
(ii)Zがn-1で割り切れるときのnの値をすべて求めると$\boxed{\ \ ト\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (7)整数Zはn進法で表すとk+1桁であり、$n^k$の位の数が4、$n^i$ (1≦i≦k-1)の位の数が0、$n^0$の位の数が1となる。ただし、nはn≧3を満たす整数、kはk≧2を満たす整数とする。
(i)k=3とする。Zをn+1で割った時の余りは$\boxed{\ \ テ\ \ }$である。
(ii)Zがn-1で割り切れるときのnの値をすべて求めると$\boxed{\ \ ト\ \ }$である。
2023慶應義塾大学薬学部過去問
横浜市立(医)整数の基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とし,$1\leqq n \leqq 1000$である.
$n^5+1$が3の倍数となるnは何個か?
横浜市立(医)過去問
この動画を見る
$n$を自然数とし,$1\leqq n \leqq 1000$である.
$n^5+1$が3の倍数となるnは何個か?
横浜市立(医)過去問
整数問題 浪速高校

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{96}{(n-1)(n+1)}$が自然数となるような自然数nは何個?
浪速高等学校
この動画を見る
$\frac{96}{(n-1)(n+1)}$が自然数となるような自然数nは何個?
浪速高等学校
不定三次方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は実数であり,
$x^3+y^3+(x+y)^3+30xy=2000$を満たすとき,$x+y=?$
この動画を見る
$x,y$は実数であり,
$x^3+y^3+(x+y)^3+30xy=2000$を満たすとき,$x+y=?$
整数問題 分けろ!!(高校数学)

大学入試問題#508「入試の1問目がこれは萎える」 防衛医科大学(2015) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$a^5-12a^4+36a^3-81a+1,\ a^2-6a$が共に有理数となる無理数$a$を求めよ
出典:2015年防衛医科大学 入試問題
この動画を見る
$a^5-12a^4+36a^3-81a+1,\ a^2-6a$が共に有理数となる無理数$a$を求めよ
出典:2015年防衛医科大学 入試問題
図形問題にみえて実は〇〇問題 慶應義塾高校

単元:
#数Ⅰ#数A#図形と計量#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
nは3以上の整数とする。
正n角形の1つの内角をx°とするときxの値が整数となる正n角形は何個?
慶應義塾高等学校
この動画を見る
nは3以上の整数とする。
正n角形の1つの内角をx°とするときxの値が整数となる正n角形は何個?
慶應義塾高等学校
一発で二重根号を外せ

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
二重根号を外せ.
$\sqrt{283-36\sqrt{30}}$
$\sqrt{111+24\sqrt{10}}$
この動画を見る
二重根号を外せ.
$\sqrt{283-36\sqrt{30}}$
$\sqrt{111+24\sqrt{10}}$
福田の数学〜慶應義塾大学2023年薬学部第1問(1)〜素因数分解と変数の値

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
=入れる入れない問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2a < x < a+3$
これを満たす整数xが4だけであるとき定数aの値の範囲は?
この動画を見る
$2a < x < a+3$
これを満たす整数xが4だけであるとき定数aの値の範囲は?
綺麗な数字の並びの平方数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
平方数であることを示せ.
$\underbrace{277 + \cdots + 7}_{n個}
\underbrace{88 + \cdots + 89}_{ n+1個}$
この動画を見る
平方数であることを示せ.
$\underbrace{277 + \cdots + 7}_{n個}
\underbrace{88 + \cdots + 89}_{ n+1個}$
整数問題・フェルマーの小定理の利用

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2023^4+1$を素因数分解したときの2以外の素因数を1つ挙げよ.
この動画を見る
$2023^4+1$を素因数分解したときの2以外の素因数を1つ挙げよ.
四捨五入

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
20で割って、小数第一位を四捨五入すると17になるような最大の整数と最小の整数を求めよ
この動画を見る
20で割って、小数第一位を四捨五入すると17になるような最大の整数と最小の整数を求めよ
関西医科大

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
この動画を見る
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
あなたもダマされる

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$x \times x = 2 \times 2$
この動画を見る
方程式を解け
$x \times x = 2 \times 2$
ただの素因数分解

整数問題
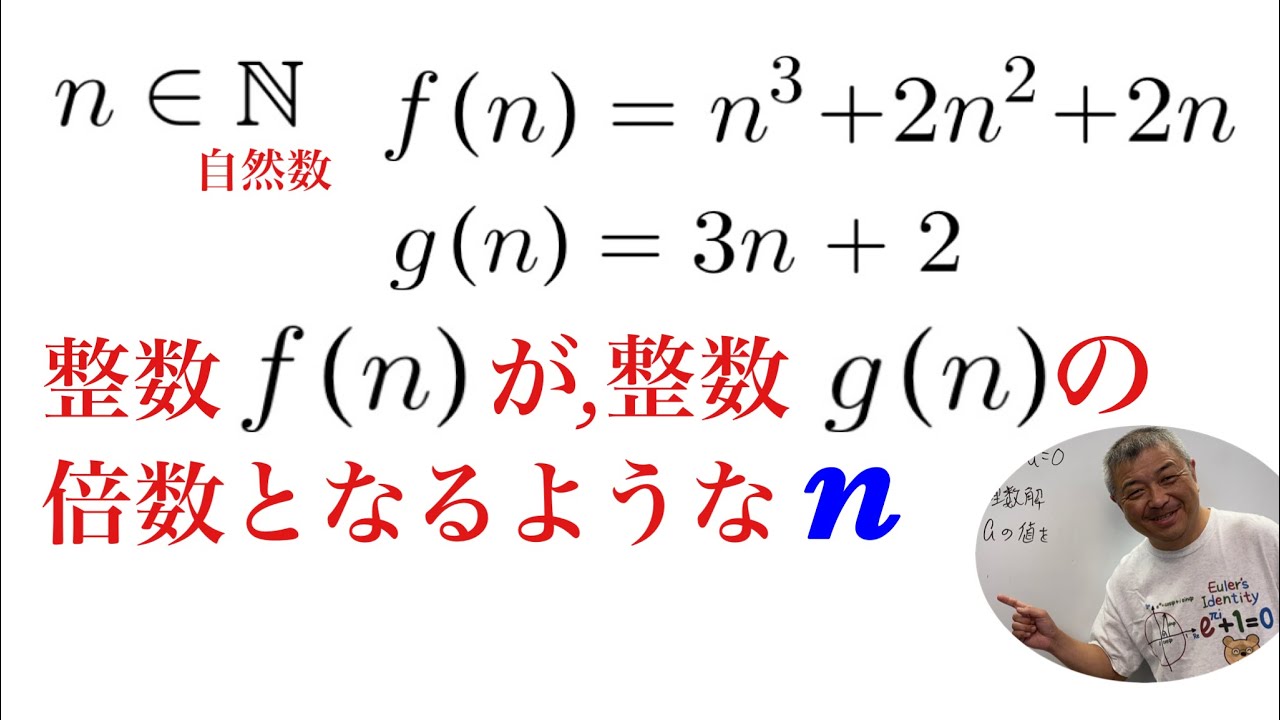
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数である.
$f(n)=n^3+2n^2+2n$
$g(n)=3n+2$
整数$f(n)$は整数$g(n)$の倍数である.
nをすべて求めよ.
この動画を見る
$n$は自然数である.
$f(n)=n^3+2n^2+2n$
$g(n)=3n+2$
整数$f(n)$は整数$g(n)$の倍数である.
nをすべて求めよ.
場合分けの嵐 新高1見て

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$(a^2-1)x^2 = a - 1$
(aは定数)
この動画を見る
方程式を解け
$(a^2-1)x^2 = a - 1$
(aは定数)
ざ・見掛け倒し

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$11^{2023}+13^{2023}を144で割った余りを求めよ.$
この動画を見る
$11^{2023}+13^{2023}を144で割った余りを求めよ.$
福田の数学〜大阪大学2023年理系第5問〜確率漸化式と整数の性質

単元:
#数A#大学入試過去問(数学)#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ 1個のさいころをn回投げて、k回目に出た目を$a_k$とする。$b_n$を
$b_n$=$\displaystyle\sum_{k=1}^na_1^{n-k}a_k$
により定義し、b_nが7の倍数とする確率を$p_n$とする。
(1)$p_1$, $p_2$を求めよ。
(2)数列$\left\{p_n\right\}$の一般項を求めよ。
2023大阪大学理系過去問
素因数分解せよ!prime factorization

