 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
福田の数学〜東京大学2023年文系第4問〜四面体の体積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
【数Ⅱ】図形と方程式:円と方程式 円上の点Pにおける接線の方程式を求めよ。例題付き!

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に(1)円$x^2+y^2=5$上の点P(1, 2)における接線の方程式、(2) 円$x^2+y^2= 36$上の点P(6, 0)における接線の方程式 も求めます。
【数Ⅱ】図形と方程式:円:円と方程式:円上の点Pにおける接線の方程式を求めよ。例題付き!
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
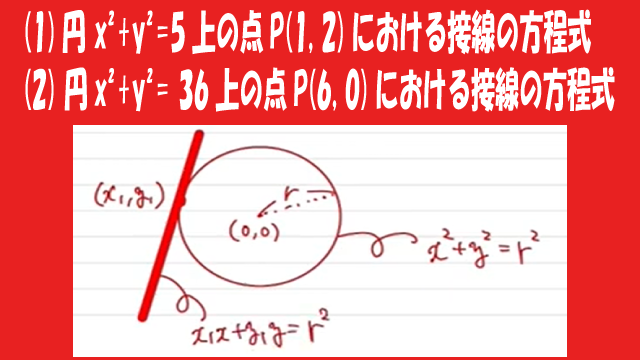
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
この動画を見る
円上の点における接線の方程式の求め方を解説!実際に
(1)円 x²+y²=5上の点P(1, 2)における接線の方程式、
(2) 円x²+y²= 36上の点P(6, 0)における接線の方程式
も求めます。
【数Ⅱ】図形と方程式:円と方程式 円の外にある点から、円に接するような直線を引け!

【数Ⅱ】図形と方程式:円:円と方程式:円の外にある点から、円に接するような直線を引け!

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
この動画を見る
点(2, 6)を通り,円x²+y²=20 に接する直線の方程式を求めよ。
【数Ⅱ】図形と方程式:円と方程式 円x^2+y^2=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
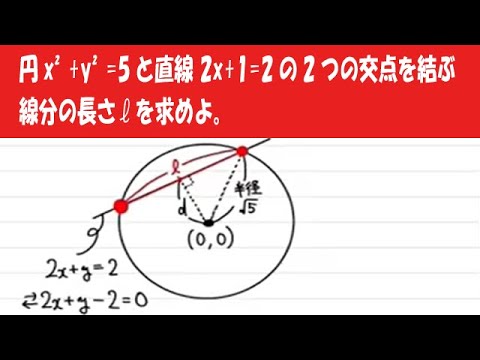
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
円$x^2+y^2=5$と直線 $2x+1=2$の2つの交点を結ぶ線分の長さlを求めよ。
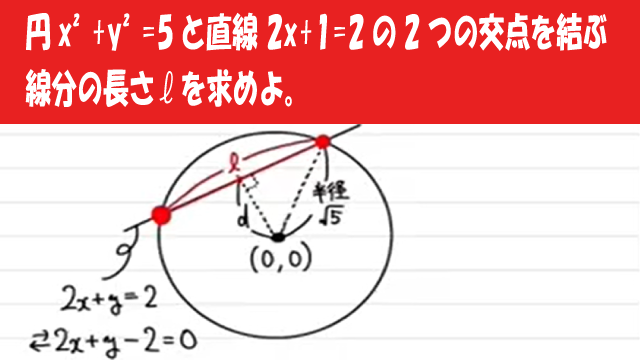
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
教材:
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
この動画を見る
【数Ⅱ】図形と方程式:円:円と方程式:円x²+y²=5と直線 2x+1=2の2つの交点を結ぶ線分の長さlを求めよ。
福田の数学〜東京大学2023年文系第2問〜定積分で表された関数と最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
福田の数学〜東京工業大学2023年理系第5問(PART1)〜4直線に接する球面の決定

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
福田の数学〜東京大学2023年理系第3問〜円と放物線と切り取られる弦の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y>x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy<aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y>x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy<aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題088〜一橋大学2018年度文系第4問〜四面体の体積の最大

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ p,qを正の実数とする。原点をOとする座標空間内の3点P(p,0,0), Q(0,q,0), R(0,0,1)は$\angle$PRQ=$\frac{\pi}{6}$を満たす。四面体OPQRの体積の最大値を求めよ。
2018一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ p,qを正の実数とする。原点をOとする座標空間内の3点P(p,0,0), Q(0,q,0), R(0,0,1)は$\angle$PRQ=$\frac{\pi}{6}$を満たす。四面体OPQRの体積の最大値を求めよ。
2018一橋大学文系過去問
【数検2級】高校数学:数学検定2級2次:問題3

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#軌跡と領域#数学検定#数学検定2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題3.(選択)
xy平面上において、点Pが円$x^2+y^2=4$上を動くとき、点A$(3,1)$と点Pを結ぶ線分APの中点Qの軌跡を求めなさい。
この動画を見る
問題3.(選択)
xy平面上において、点Pが円$x^2+y^2=4$上を動くとき、点A$(3,1)$と点Pを結ぶ線分APの中点Qの軌跡を求めなさい。
福田の1.5倍速演習〜合格する重要問題083〜東北大学2018年度理系第1問〜直線の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ xy平面上における2つの放物線C:y=$(x-a)^2+b$, D:y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
この動画を見る
$\Large\boxed{1}$ xy平面上における2つの放物線C:y=$(x-a)^2+b$, D:y=$-x^2$を考える。
(1)CとDが異なる2点で交わり、その2交点のx座標の差が1となるように実数a,bが動くとき、Cの頂点(a, b)の軌跡を図示せよ。
(2)実数a, bが(1)の条件を満たしながら動くとき、CとDの2交点を結ぶ直線が通過する範囲を定め、図示せよ。
2018東北大学理系過去問
福田の1.5倍速演習〜合格する重要問題099〜早稲田大学2020年度社会科学部第3問〜複数の円の位置関係

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上の5つの点$P_1$($-\sqrt 5$, 0), $P_2$($-\frac{\sqrt 5}{2}$, $-\frac{\sqrt 3}{2}$), $P_3$(0, 0), $P_4$($\frac{\sqrt 5}{2}$, $-\frac{\sqrt 3}{2}$), $P_5$($\sqrt 5$, 0)をそれぞれ中心とする半径1の円を$C_1$, $C_2$, $C_3$, $C_4$, $C_5$とする。次の問に答えよ。
(1)1つ以上の円に囲まれる領域の面積を求めよ。
(2)2つ以上の円と接する直線の本数を求めよ。
(3)3つ以上の円と外接する円の半径をすべて求めよ。
2020早稲田大学社会科学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の5つの点$P_1$($-\sqrt 5$, 0), $P_2$($-\frac{\sqrt 5}{2}$, $-\frac{\sqrt 3}{2}$), $P_3$(0, 0), $P_4$($\frac{\sqrt 5}{2}$, $-\frac{\sqrt 3}{2}$), $P_5$($\sqrt 5$, 0)をそれぞれ中心とする半径1の円を$C_1$, $C_2$, $C_3$, $C_4$, $C_5$とする。次の問に答えよ。
(1)1つ以上の円に囲まれる領域の面積を求めよ。
(2)2つ以上の円と接する直線の本数を求めよ。
(3)3つ以上の円と外接する円の半径をすべて求めよ。
2020早稲田大学社会科学部過去問
福田の1.5倍速演習〜合格する重要問題097〜早稲田大学2020年度教育学部第4問〜曲線の通過範囲の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面上で、定数k>0に対し、曲線y=$\frac{k}{\sqrt{1+x^2}}$の0≦x≦1の部分を$C_k$とする。
(1)曲線$C_k$上の点と原点との距離の最大値$M(k)$を求めよ。
(2)原点を中心に曲線$C_k$を1回転させるとき、$C_k$が通る部分の面積$S(k)$を求めよ。
2020早稲田大学教育学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面上で、定数k>0に対し、曲線y=$\frac{k}{\sqrt{1+x^2}}$の0≦x≦1の部分を$C_k$とする。
(1)曲線$C_k$上の点と原点との距離の最大値$M(k)$を求めよ。
(2)原点を中心に曲線$C_k$を1回転させるとき、$C_k$が通る部分の面積$S(k)$を求めよ。
2020早稲田大学教育学部過去問
福田の1.5倍速演習〜合格する重要問題071〜東京医科歯科大学2017年度医学部第2問〜空間における球面と軌跡の問題

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
福田の1.5倍速演習〜合格する重要問題064〜明治大学2019年度理工学部第2問〜円と放物線の位置関係

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$ a,bは実数でa>0とする。座標平面上において、円$x^2$+$y^2$=1を$C$とし、放物線y=a$x^2$+bを$D$とする。
(1)放物線$D$の頂点のy座標が正であり、円$C$と放物線$D$の共有点がただ一つであるとき、bの値は$\boxed{\ \ あ\ \ }$である。
(2)放物線$D$の頂点のy座標が負であり、円$C$と放物線$D$の共有点がただ一つであるとき、bの値は$\boxed{\ \ い\ \ }$であり、aの取り得る値の範囲は$\boxed{\ \ う\ \ }$である。
(3)放物線$D$の頂点が円$C$の内部にあり、円$C$と放物線$D$がちょうど2つの共有点をもつとき、bの取り得る値の範囲は$\boxed{\ \ え\ \ }$である。
(4)放物線$D$の頂点が円$C$の外部にあり、円$C$と放物線$D$がちょうど2つの共有点をもつとき、bをaの式で表すとb=$\boxed{\ \ お\ \ }$となり、aの取り得る値の範囲は$\boxed{\ \ か\ \ }$である。
2019明治大学理工学部過去問
この動画を見る
$\boxed{2}$ a,bは実数でa>0とする。座標平面上において、円$x^2$+$y^2$=1を$C$とし、放物線y=a$x^2$+bを$D$とする。
(1)放物線$D$の頂点のy座標が正であり、円$C$と放物線$D$の共有点がただ一つであるとき、bの値は$\boxed{\ \ あ\ \ }$である。
(2)放物線$D$の頂点のy座標が負であり、円$C$と放物線$D$の共有点がただ一つであるとき、bの値は$\boxed{\ \ い\ \ }$であり、aの取り得る値の範囲は$\boxed{\ \ う\ \ }$である。
(3)放物線$D$の頂点が円$C$の内部にあり、円$C$と放物線$D$がちょうど2つの共有点をもつとき、bの取り得る値の範囲は$\boxed{\ \ え\ \ }$である。
(4)放物線$D$の頂点が円$C$の外部にあり、円$C$と放物線$D$がちょうど2つの共有点をもつとき、bをaの式で表すとb=$\boxed{\ \ お\ \ }$となり、aの取り得る値の範囲は$\boxed{\ \ か\ \ }$である。
2019明治大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題061〜早稲田大学2019年度社会科学部第1問〜円の通過範囲と放物線と円の位置関係

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#大学入試解答速報#数学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $k$を実数とする。座標平面において方程式
$x^2+y^2+x+(2k+1)y+k^2+1=0$
の表す図形$C$を考える。次の問いに答えよ。
(1)$C$が円であるような$k$の値の範囲を求めよ。ただし、点も円とみなすものとする。
(2)$k$が変化するとき、$C$が通る点($x,y$)の存在領域を座標平面上に図示せよ。
(3)(2)で求めた領域の境界線と(1)で求めた円が共有点をもたないような、$k$の値の
範囲を求めよ。
2019早稲田大学社会科学部過去問
この動画を見る
$\Large{\boxed{1}}$ $k$を実数とする。座標平面において方程式
$x^2+y^2+x+(2k+1)y+k^2+1=0$
の表す図形$C$を考える。次の問いに答えよ。
(1)$C$が円であるような$k$の値の範囲を求めよ。ただし、点も円とみなすものとする。
(2)$k$が変化するとき、$C$が通る点($x,y$)の存在領域を座標平面上に図示せよ。
(3)(2)で求めた領域の境界線と(1)で求めた円が共有点をもたないような、$k$の値の
範囲を求めよ。
2019早稲田大学社会科学部過去問
福田の1.5倍速演習〜合格する重要問題059〜慶應義塾大学2019年度薬学部第1問(7)〜球に内接する四角錐の体積の最大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
この動画を見る
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
福田の1.5倍速演習〜合格する重要問題058〜慶應義塾大学2019年度環境情報学部第5問〜正方形の中の内接外接する円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
この動画を見る
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
福田の1.5倍速演習〜合格する重要問題049〜早稲田大学2019年度商学部第2問〜折れ線の長さの最小値問題

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#図形と方程式#微分法と積分法#点と直線#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
この動画を見る
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
福田の1.5倍速演習〜合格する重要問題047〜慶應義塾大学2019年度総合政策学部第3問〜立方体の内部を面に接しながら動く球の通過できない領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
一辺の長さが2である立方体ABCD-EFGHの内部に半径rの球$S(r \gt 0)$が
存在する。球Sは立方体ABCD-EFGHの少なくとも1つの面と接しながら動く。
このとき、立方体ABCD-EFGHの内部で球Sが通過しえない領域の体積Vは
$(\textrm{i})0 \lt r \lt \frac{\boxed{ア}}{\boxed{イ}}$のとき
$V=\left(\boxed{ウエオ}+\frac{\boxed{カキ}}{\boxed{クケ}}\pi\right)r^3+$
$(\boxed{コサシ}+\boxed{スセ}\pi)r^2$
$+\boxed{ソタチ}r+\boxed{ツテ}$
$(\textrm{ii})\frac{\boxed{ア}}{\boxed{イ}} \leqq r \leqq 1$のとき
$V=\left(\boxed{トナニ}+\frac{\boxed{ヌネ}}{\boxed{ノハ}}\pi\right)r^3+$
$(\boxed{ヒフヘ}+\boxed{ホマ}\pi)r^2$
2019慶應義塾大学総合政策学部過去問
この動画を見る
一辺の長さが2である立方体ABCD-EFGHの内部に半径rの球$S(r \gt 0)$が
存在する。球Sは立方体ABCD-EFGHの少なくとも1つの面と接しながら動く。
このとき、立方体ABCD-EFGHの内部で球Sが通過しえない領域の体積Vは
$(\textrm{i})0 \lt r \lt \frac{\boxed{ア}}{\boxed{イ}}$のとき
$V=\left(\boxed{ウエオ}+\frac{\boxed{カキ}}{\boxed{クケ}}\pi\right)r^3+$
$(\boxed{コサシ}+\boxed{スセ}\pi)r^2$
$+\boxed{ソタチ}r+\boxed{ツテ}$
$(\textrm{ii})\frac{\boxed{ア}}{\boxed{イ}} \leqq r \leqq 1$のとき
$V=\left(\boxed{トナニ}+\frac{\boxed{ヌネ}}{\boxed{ノハ}}\pi\right)r^3+$
$(\boxed{ヒフヘ}+\boxed{ホマ}\pi)r^2$
2019慶應義塾大学総合政策学部過去問
福田の1.5倍速演習〜合格する重要問題041〜上智大学2019年度TEAP文系第3問〜長方形の紙を折り返す問題

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
この動画を見る
$AB=2,BC=3$の長方形ABCDの形の紙がある。DE=aとなる辺DC上の
点Eを考える。AがEと重なるように紙を折るとき、折り目となる線と辺AD,
辺BCとの交点をそれぞれP,Qとする。
(1)aを用いて表すと、$AP=\frac{\boxed{二}}{\boxed{ヌ}}a^2+\frac{\boxed{ネ}}{\boxed{ノ}}$である.
(2)aを用いて表すと、$BQ=\frac{\boxed{ハ}}{\boxed{ヒ}}a^2+
\frac{\boxed{フ}}{\boxed{ヘ}}a+\frac{\boxed{ホ}}{\boxed{マ}}$である。
(3)aを用いて表すと、$PQ=\frac{\boxed{ミ}}{\boxed{ム}}\sqrt{a^2+\boxed{メ}}$である。
(4)四角形ABQPの面積はaを用いて表すと、$\frac{\boxed{モ}}{\boxed{ヤ}}a^2+\frac{\boxed{ユ}}{\boxed{ヨ}}a+\boxed{ラ}$
であり、その最小値は$\frac{\boxed{リ}}{\boxed{ル}}$である。
2019上智大過去問
福田の1.5倍速演習〜合格する重要問題030〜東京大学2016年度文系第1問〜鋭角三角形となる条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上のベクトル#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
この動画を見る
座標平面上の3点$P(x,y), Q(-x,-y), R(1,0)$が鋭角三角形をなすための$(x,y)$
についての条件を求めよ。また、その条件を満たす点P(x,y)の範囲を図示せよ。
2016東京大学文系過去問
福田の1.5倍速演習〜合格する重要問題025〜大阪大学2016年度理系数学第3問〜回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点Oを中心とする半径rの円と放物線$y=\sqrt2(x-1)^2$
は、ただ1つの共有点(a,b)をもつとする。
(1)a,b,rの値をそれぞれ求めよ。
(2)連立不等式
$a \leqq x \leqq 1, 0 \leqq y \leqq \sqrt2(x-1)^2, x^2+y^2 \geqq r^2$
の表す領域をx軸のまわりに1回転してできる回転体の体積を求めよ。
2016大阪大学理系過去問
この動画を見る
座標平面において、原点Oを中心とする半径rの円と放物線$y=\sqrt2(x-1)^2$
は、ただ1つの共有点(a,b)をもつとする。
(1)a,b,rの値をそれぞれ求めよ。
(2)連立不等式
$a \leqq x \leqq 1, 0 \leqq y \leqq \sqrt2(x-1)^2, x^2+y^2 \geqq r^2$
の表す領域をx軸のまわりに1回転してできる回転体の体積を求めよ。
2016大阪大学理系過去問
福田の1.5倍速演習〜合格する重要問題024〜名古屋大学2016年度理系数学第1問〜垂直条件と解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#図形と方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
曲線$y=x^2$上に2点$A(-2,4),B(b,b^2)$をとる。ただし、$b \gt -2$とする。
このとき、次の条件を満たすbの範囲を求めよ。
条件:$y=x^2$上の点$T(t,t^2)(-2 \lt t \lt b)$で、$\angle ATB$が直角になるものが
存在する。
2016名古屋大学理系過去問
この動画を見る
曲線$y=x^2$上に2点$A(-2,4),B(b,b^2)$をとる。ただし、$b \gt -2$とする。
このとき、次の条件を満たすbの範囲を求めよ。
条件:$y=x^2$上の点$T(t,t^2)(-2 \lt t \lt b)$で、$\angle ATB$が直角になるものが
存在する。
2016名古屋大学理系過去問
福田の1.5倍速演習〜合格する重要問題012〜京都大学2015年度文系数学第1問〜折れ線と交わらない条件

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次関数とグラフ#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
この動画を見る
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
福田の1.5倍速演習〜合格する重要問題008〜神戸大学文系数学第1問〜対称式と軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#平面上のベクトル#図形と方程式#解と判別式・解と係数の関係#軌跡と領域#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
s,tを$s \lt t$をみたす実数とする。座標平面上の3点$A(1,2),B(s,s^2),C(t,t^2)$が一直線上にあるとする。以下の問いに答えよ。
(1)sとtの関係式を求めよ。
(2)線分BCの中点をM(u,v)とする。uとvの間の関係式を求めよ。
(3)s,tが変化するとき、vの最小値と、その時のu,s,tの値を求めよ。
神戸大学文系過去問
この動画を見る
s,tを$s \lt t$をみたす実数とする。座標平面上の3点$A(1,2),B(s,s^2),C(t,t^2)$が一直線上にあるとする。以下の問いに答えよ。
(1)sとtの関係式を求めよ。
(2)線分BCの中点をM(u,v)とする。uとvの間の関係式を求めよ。
(3)s,tが変化するとき、vの最小値と、その時のu,s,tの値を求めよ。
神戸大学文系過去問
放物線と直線
単元:
#数学(中学生)#数Ⅱ#図形と方程式#点と直線#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
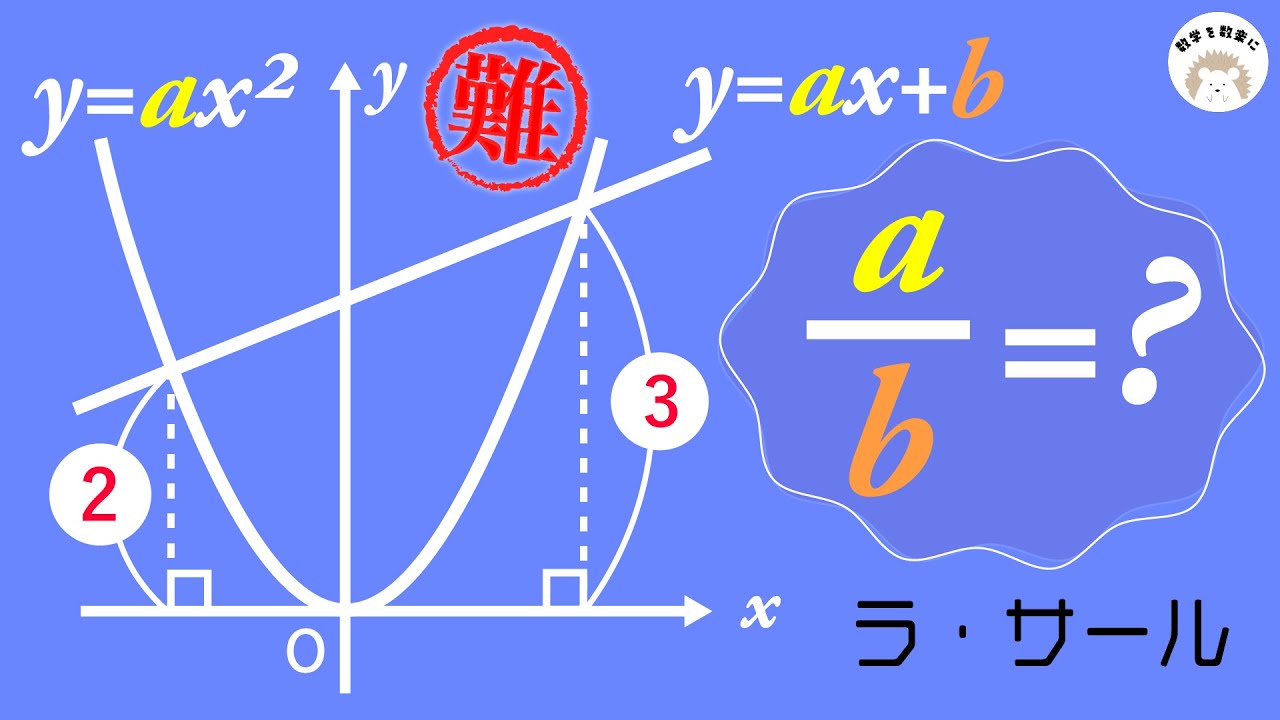
$\frac{a}{b}=?$
*図は動画内参照
ラ・サール高等学校
この動画を見る
$\frac{a}{b}=?$
*図は動画内参照
ラ・サール高等学校
福田の1.5倍速演習〜合格する重要問題001〜東京大学2015年理系問題1〜放物線の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
問題文全文(内容文):
正の実数aに対して、座標平面上で次の放物線を考える。
$C:\ y=ax^2+\frac{1-4a^2}{4a}$aが正の実数全体を動くとき、Cの通過する領域を図示せよ。
2015東京大学理系過去問
この動画を見る
正の実数aに対して、座標平面上で次の放物線を考える。
$C:\ y=ax^2+\frac{1-4a^2}{4a}$aが正の実数全体を動くとき、Cの通過する領域を図示せよ。
2015東京大学理系過去問
