 平均変化率・極限・導関数
平均変化率・極限・導関数
 平均変化率・極限・導関数
平均変化率・極限・導関数
福田のおもしろ数学537〜2変数関数の極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
この動画を見る
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
福田のおもしろ数学532〜「∞ー∞」型の極限
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
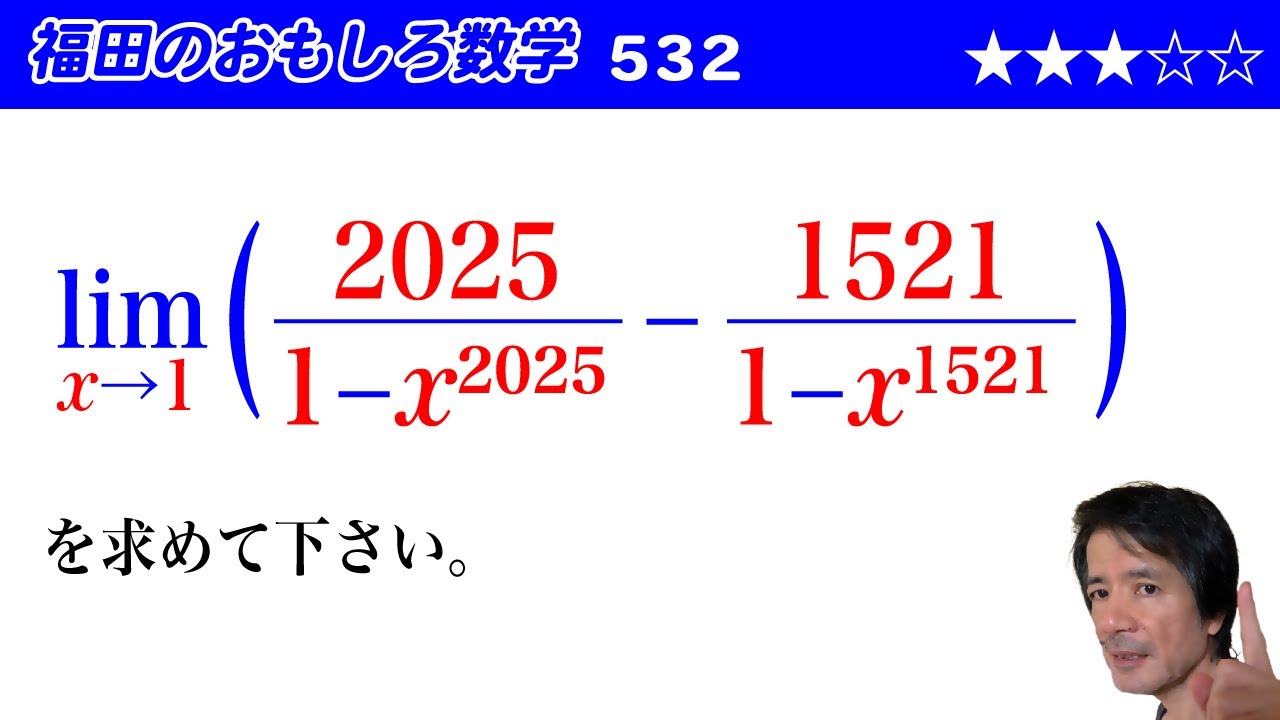
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
福田のおもしろ数学524〜無限級数の和

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
福田のおもしろ数学518〜積分で表された関数の導関数

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#不定積分・定積分#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
この動画を見る
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
福田のおもしろ数学506〜相加平均と相乗平均の商の極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。
この動画を見る
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。
福田の数学〜慶應義塾大学看護医療学部2025第2問(1)〜極形式とド・モアブルの定理

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
この動画を見る
$\boxed{2}$
(1)$x^3-3x^2+6x-4=0$の解で
虚部が正であるものを$\omega$としたとき、
$\omega$の絶対値は$\vert \omega \vert=\boxed{キ}$であり、
偏角$\theta$は$\theta=\boxed{ク}$である。
ただし、$0\leqq \theta \lt 2\pi$とする。
また、$\omega^{10} =\boxed{ケ}+\boxed{コ}i$である。
ただし、$\boxed{ケ},\boxed{コ}$は実数とする。
$2025$年慶應義塾大学看護医療学部過去問題
福田の数学〜東北大学2025理系第4問〜2曲線の相接と面積の極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$n$を正の整数、$a$を正の実数とし、
関数$f(x)$と$g(x)$を次のように定める。
$f(x)=n\log x,\quad g(x)=ax^n$
また、曲線$y=f(x)$と曲線$y=g(x)$が共有点をもち、
その共有点における
$2$つの曲線の接線が一致しているとする。
このとき、以下の問いに答えよ。
(1)$a$の値を求めよ。
(2)この$2$つの曲線と$x$軸で囲まれた部分の面積
$S_n$を求めよ。
(3)$\quad $(2)で求めた$S_n$に対し、極限$\displaystyle \lim_{n\to\infty}S_n$を求めよ。
$2025$年東北大学理系過去問題
この動画を見る
$\boxed{4}$
$n$を正の整数、$a$を正の実数とし、
関数$f(x)$と$g(x)$を次のように定める。
$f(x)=n\log x,\quad g(x)=ax^n$
また、曲線$y=f(x)$と曲線$y=g(x)$が共有点をもち、
その共有点における
$2$つの曲線の接線が一致しているとする。
このとき、以下の問いに答えよ。
(1)$a$の値を求めよ。
(2)この$2$つの曲線と$x$軸で囲まれた部分の面積
$S_n$を求めよ。
(3)$\quad $(2)で求めた$S_n$に対し、極限$\displaystyle \lim_{n\to\infty}S_n$を求めよ。
$2025$年東北大学理系過去問題
福田の数学〜北海道大学2025理系第3問〜部分積分と極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{3}$
実数$a$および自然数$n$に対して、定積分
$I(a,n)=\displaystyle \int_{0}^{2\pi} e^{ax} \sin (nx) dx$
を考える。ここで$e$は自然対数の底である。
(1)$I(a,n)$を求めよ。
(2)$a_n=\dfrac{\log _n}{2\pi} (n=1,2,3,\cdots)$のとき、
極限$\displaystyle \lim_{n\to\infty} I(a_n,n)$を求めよ。
ただし、$\log_n$は$n$の自然対数である。
また、必要ならば$\displaystyle \lim_{n\to\infty}\dfrac{\log_n}{n}=0$である
ことを用いてもよい。
$2025$年北海道大学理系過去問題
福田の数学〜東京大学2025理系第2問〜はさみうちの原理を利用する極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
【数Ⅱ】【微分法と積分法】極値の場合分け ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a<0
(2)a=0
(3)a>0
この動画を見る
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a<0
(2)a=0
(3)a>0
【数Ⅱ】【微分法と積分法】極値を持つ条件 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
この動画を見る
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
【数Ⅱ】【微分法と積分法】微分の基本6 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
この動画を見る
$k$は0ではない定数とする。次の等式を満たす2次関数$f(x)$を求めよ。
$f(x)-x^2f'(x)=k^2x^3-kx+5$
【数Ⅱ】【微分法と積分法】微分の基本5 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
この動画を見る
次の関数を求めよ。
(1) 等式 $f(x)+(x+2)f'(x)=9x^2+8x-3$ を満たす2次関数$f(x)$
(2) 等式 $g(x)+xg'(x)=4x^3+6x^2+4x+1$ を満たす3次関数$g(x)$
【数Ⅱ】【微分法と積分法】微分の基本4 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき,$S$を$x$の関数で表せ。
(2)$x$が変化するとき,$S$の$x=5$における微分係数を求めよ。
この動画を見る
1辺の長さ$x$の正四面体がある。
(1)正四面体の表面積を$S$とするとき,$S$を$x$の関数で表せ。
(2)$x$が変化するとき,$S$の$x=5$における微分係数を求めよ。
【数Ⅱ】【微分法と積分法】微分の基本3 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
この動画を見る
$\{(ax+b)^n\}'=na(ax+b)^{n-1}$ ($n$ は正の整数) であることを用いて、次の関数を微分せよ。
$(1)\ y=(2x+1)^3$
$(2)\ y=(x-1)^4$
$(3)\ y=(-2x+1)^5$
【数Ⅱ】【微分法と積分法】微分の基本2 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
この動画を見る
$f(x)=x^2-3x$ とする。
関数 $y=f(x)$ のグラフ上の2点 $(1,\,f(1)),\ (a,\,f(a))$ を結ぶ直線の傾きが、$x=b$ $(1< b < a)$ における微分係数 $f'(b)$ に等しい。
$b$ を $a$ で表せ。
【数Ⅱ】【微分法と積分法】微分の基本1 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
この動画を見る
次の関数 $f(x)$ について、$x=a$ における微分係数 $f'(x)$ を求めよ。また、$f'(a)$ が、$x$ が $0$ から $2$ まで変化するときの平均変化率に一致するとき、$a$ の値を求めよ。
$(1)\ f(x)=x^2-x$
$(2)\ f(x)=x^3-x^2+1$
【数Ⅱ】【微分法と積分法】極限の計算 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
この動画を見る
(1)$\displaystyle \lim_{ x \to -2 } (x^2+1)(x-1)$
(2)$\displaystyle \lim_{ x \to 1 } (x^3-1)(x-1)$
(3)$\displaystyle \lim_{ x \to 2 } (x^2-x-2)(x^2+x-6)$
(4)$\displaystyle \lim_{ x \to -3 } \frac{1}{x+3}(\frac{12}{x-3}+2)$
#高専 #極限_75

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{1}{\sqrt{n^2+kn}}$を解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{1}{\sqrt{n^2+kn}}$を解け.
#電気通信大学2024#極限_72

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \displaystyle \sum_{k=1}^{n} \dfrac{n}{n^2+3k^2}$を解け.
電気通信大学過去問題
福田のおもしろ数学264〜なぜ球の表面積は4πr^3なのかの証明

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
半径$r$の球の体積が$\frac{4πr^3}{3}$あることを既知として、表面積が$4πr^2$であることを証明して下さい。
この動画を見る
半径$r$の球の体積が$\frac{4πr^3}{3}$あることを既知として、表面積が$4πr^2$であることを証明して下さい。
福田のおもしろ数学260〜関数方程式を満たす関数を探せ

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
微分可能な関数 $f(x)$ はすべての実数 $x,y$ に対し
$f(x^2-y^2)$$=xf(x)-yf(y)$ $\cdots$ ① を満たす。このような $f(x)$ をすべて求めて下さい。
この動画を見る
微分可能な関数 $f(x)$ はすべての実数 $x,y$ に対し
$f(x^2-y^2)$$=xf(x)-yf(y)$ $\cdots$ ① を満たす。このような $f(x)$ をすべて求めて下さい。
#福岡大学医学部2018#極限_61
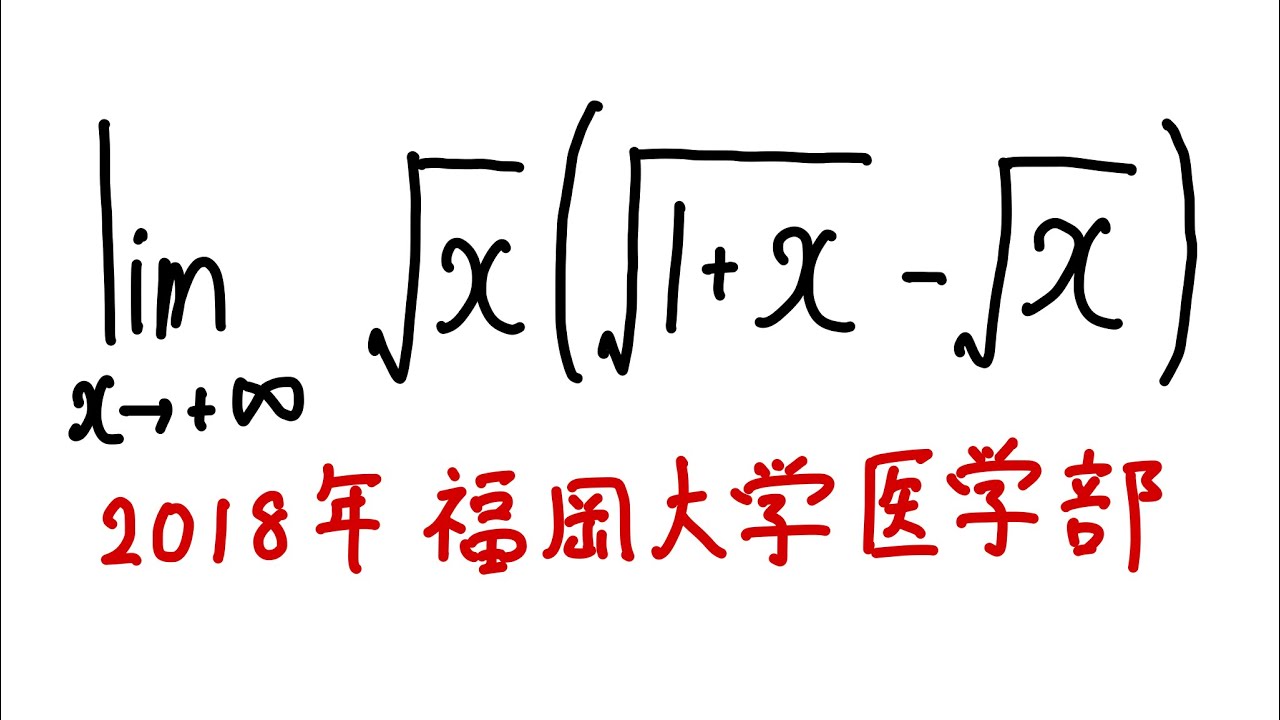
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} \sqrt x \left(\sqrt{1+x}-\sqrt x \right)$を解け.
2018福岡大学医学部過去問題
うおおおおお! 東京都市大学(武蔵工業大学)2004 大学入試問題#934

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#武蔵工業大学
指導講師:
ますただ
問題文全文(内容文):
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
この動画を見る
連続関数$f(x)$で
$f(x)=e^x \displaystyle \int_{0}^{1} \{f(t)\}^2 dt$
を満たすものを求めよ.
2004東京都市大学過去問題
#京都大学1937#極限_59

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
この動画を見る
$\displaystyle \lim_{x\to\infty} x \sin \dfrac{a}{x}$を解け.
1937京都帝国大学過去問題
#三重大学医学部2023#極限_50

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n\{ \log n-\log (n+1)\}}{\log n}{\log n}$
を解け.
2023三重大学医学部過去問題
#明治大学2023#極限_48

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
この動画を見る
$f(x)=\log (2e^{3x}+4)-ax-b$が
$\displaystyle \lim_{x\to\infty} \ f(x)=0$のとき,
$a,b$の値を求めよ.
2023明治大学過去問題
#産業医科大学2024#区分級積法_41

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
#茨城大学2022#極限_10#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典:2022年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to -\infty } \displaystyle \frac{4^{x+2}+2^{x-2}}{4^x-2^x}$
出典:2022年茨城大学
大学入試問題#907「チャートに掲載されてる?」 #信州大学理学部(2024) #極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to a } \displaystyle \frac{x^3-x^2+(2a-3)x+b}{x^2-(a-1)x-a}=3$
が成り立つように定数$a$と$b$の値を求めよ。
出典:2024年信州大学理学部
この動画を見る
$\displaystyle \lim_{ x \to a } \displaystyle \frac{x^3-x^2+(2a-3)x+b}{x^2-(a-1)x-a}=3$
が成り立つように定数$a$と$b$の値を求めよ。
出典:2024年信州大学理学部
