接線と増減表・最大値・最小値
接線と増減表・最大値・最小値
【数Ⅱ】【微分法と積分法】接線からの関数決定 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
この動画を見る
$f'(x)=x^2+2x+2$で、曲線$y=f(x)$は$y=-3x+1$に接している。この時、$f(x)$を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数5 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
この動画を見る
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数8 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
この動画を見る
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数7 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数6 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
この動画を見る
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件2 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように，定数aの値の範囲を定めよ。
この動画を見る
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように，定数aの値の範囲を定めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件1 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数f(x)=x³+ax²+bx+cについて，次の問に答えよ。
（１）x=1で極大となるための条件を求めよ。
（２）x=-2で極小となるための条件を求めよ。
この動画を見る
関数f(x)=x³+ax²+bx+cについて，次の問に答えよ。
（１）x=1で極大となるための条件を求めよ。
（２）x=-2で極小となるための条件を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線7 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの曲線y=x²，y=-(x-2)²の共通接線の方程式を求めよ。
この動画を見る
2つの曲線y=x²，y=-(x-2)²の共通接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線6 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの曲線y=x²+2，y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき，定数aの値を求めよ。
この動画を見る
2つの曲線y=x²+2，y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき，定数aの値を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線5 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき，定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は，ともにある点Pを通り，Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
この動画を見る
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき，定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は，ともにある点Pを通り，Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線4 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=2x²-4x+3上の点A(0,3)を通り，点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
この動画を見る
曲線y=2x²-4x+3上の点A(0,3)を通り，点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線3 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=-x³+4x上の点(-2,0)における接線が，この曲線と交わるもう1つの点のx座標を求めよ。
この動画を見る
曲線y=-x³+4x上の点(-2,0)における接線が，この曲線と交わるもう1つの点のx座標を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線2 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
曲線y=x³+3x²-6 について，傾きが9である接線の方程式を求めよ。
この動画を見る
曲線y=x³+3x²-6 について，傾きが9である接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線1 ※問題文は概要欄
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の曲線に，与えられた点から引いた接線の方程式と，接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
この動画を見る
次の曲線に，与えられた点から引いた接線の方程式と，接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
微分法と積分法 数Ⅱ 絶対値を含む関数の最大最小【マコちゃんねるがていねいに解説】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
関数f(x)=│x(x-1)(x-2)│ (-1≦x≦3) の最大値，最小値を求めよ。
この動画を見る
関数f(x)=│x(x-1)(x-2)│ (-1≦x≦3) の最大値，最小値を求めよ。
微分法と積分法 数Ⅱ 複合関数の最大最小【マコちゃんねるがていねいに解説】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
x+3y=9，x≧0，y≧0のとき，x²yの最大値，最小値を求めたい。
(1) x²yをxだけの式で表せ。
(2) xの取り得る範囲を求めよ。
(3) x²yの最大値と最小値と，そのときのx，yの値を求めよ。
この動画を見る
x+3y=9，x≧0，y≧0のとき，x²yの最大値，最小値を求めたい。
(1) x²yをxだけの式で表せ。
(2) xの取り得る範囲を求めよ。
(3) x²yの最大値と最小値と，そのときのx，yの値を求めよ。
微分法と積分法 数Ⅱ 最大最小を利用した関数の決定2【マコちゃんねるがていねいに解説】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
a,bは定数で、a＞0とする。関数f(x)=ax⁴-4ax³+b (1≦x≦4) の最大値が9、最小値がｰ18になるように,定数a,bの値を定めよ。
この動画を見る
a,bは定数で、a＞0とする。関数f(x)=ax⁴-4ax³+b (1≦x≦4) の最大値が9、最小値がｰ18になるように,定数a,bの値を定めよ。
福田の数学〜東京理科大学2024創域理工学部第2問〜放物線の接線と極限
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$m$を正の実数とし、関数$f(x)$を$f(x)=-mx^2+1$と定める。座標平面上の曲線$y=f(x)$を$C$とおき、負の実数$a$に対して点$\textrm{A}(a,f(a))$における曲線$C$の接線を$l_1$とおく。直線$l_1$と$y$軸との交点を$\textrm{P}$とし、点$\textrm{P}$を通り$l_1$に垂直な直線を$l_2$とおき、$l_2$と$x$軸の交点を$\textrm{Q}$とする。
(1) 点$\textrm{P}$の座標を$a$と$m$を用いて表せ。
(2) 点$\textrm{Q}$の座標を$a$と$m$を用いて表せ。
以下、直線$l_2$が曲線$C$の接線となるときを考える。
(3) $a$を$m$を用いて表せ。
(4) 線分$\textrm{AQ}$の長さは$m$を用いて表される。これを$L(m)$とおく。
(a) $\displaystyle \lim_{m \rightarrow \infty}L(m)$を求めよ。
(b) $\displaystyle \lim_{m \rightarrow 0}mL(m)$を求めよ。
この動画を見る
$m$を正の実数とし、関数$f(x)$を$f(x)=-mx^2+1$と定める。座標平面上の曲線$y=f(x)$を$C$とおき、負の実数$a$に対して点$\textrm{A}(a,f(a))$における曲線$C$の接線を$l_1$とおく。直線$l_1$と$y$軸との交点を$\textrm{P}$とし、点$\textrm{P}$を通り$l_1$に垂直な直線を$l_2$とおき、$l_2$と$x$軸の交点を$\textrm{Q}$とする。
(1) 点$\textrm{P}$の座標を$a$と$m$を用いて表せ。
(2) 点$\textrm{Q}$の座標を$a$と$m$を用いて表せ。
以下、直線$l_2$が曲線$C$の接線となるときを考える。
(3) $a$を$m$を用いて表せ。
(4) 線分$\textrm{AQ}$の長さは$m$を用いて表される。これを$L(m)$とおく。
(a) $\displaystyle \lim_{m \rightarrow \infty}L(m)$を求めよ。
(b) $\displaystyle \lim_{m \rightarrow 0}mL(m)$を求めよ。
微分法と積分法 数Ⅱ 最大最小を利用した関数の決定【マコちゃんねるがていねいに解説】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#微分法と積分法#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
a,bは定数で、a＜0とする。関数f(x)=ax³-3ax²+b (1≦x≦3) の最大値が10,最小値が-2になるように,定数a,bの値を定めよ。
この動画を見る
a,bは定数で、a＜0とする。関数f(x)=ax³-3ax²+b (1≦x≦3) の最大値が10,最小値が-2になるように,定数a,bの値を定めよ。
福田の数学〜明治大学2024全学部統一IⅡAB第1問(1)〜接線と法線の方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
この動画を見る
座標平面上の放物線 $y=2x^2-1$ を考える。 $t$ を $0$ でない定数とするとき、放物線上の点 $\mathrm{P}(t,2t^2-1)$ における接線 $l$ の方程式は
$y=\fbox{ア}x $$- \fbox{イ}t^2 $$- \fbox{ウ}$
である。点 $\mathrm{P}$ を通りこの接線 $l$ に直交する直線を点 $\mathrm{P}$ における法線と呼ぶことにすると、この法線の方程式は
$y=\fbox{エ}x $$+ \fbox{オ}t^2 $$- \frac{\fbox{カ}}{\fbox{キ}}$ である。
ア、エの解答群は動画内参照。
大学入試問題#902「いやーこれはしんどかった」 #東京理科大学(2010)
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
点$(x,y)$は$x^2+y^2=1$を満たしているとき
$\displaystyle \frac{2x+y+1}{3x+y+5}$の最大値と最小値を求めよ。
出典：2010年東京理科大学
この動画を見る
点$(x,y)$は$x^2+y^2=1$を満たしているとき
$\displaystyle \frac{2x+y+1}{3x+y+5}$の最大値と最小値を求めよ。
出典：2010年東京理科大学
福田の数学〜筑波大学2024理系第3問〜3次関数のグラフと接線
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
この動画を見る
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
福田のおもしろ数学211〜証明しやすく変形するコツ〜不等式の証明
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
この動画を見る
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
福田の数学〜立教大学2024年経済学部第2問〜接線が作る三角形の面積の最小値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
この動画を見る
$p,q$を正の定数とする。座標平面上に放物線$C:y=-x^2$がある。$C$上の点$\mathrm{P}(p,-p^2)$における$C$の接線を$l$,$\mathrm{Q}(q,-q^2)$における$C$の接線を$m$とする。また$l$と$m$の交点を$\mathrm{R}$とする。
(1) $l,m$の方程式をそれぞれ求めよ。
(2) $\mathrm{R}$の座標を$p,q$を用いて表せ。
(3) $\mathrm{Q}$と$l$の距離$d$を$p,q$を用いて表せ。
(4) 三角形$\mathrm{PQR}$の面積$S$を$p,q$を用いて表せ。
(5) $l$と$m$が直交するとき、$q$を$p$を用いて表せ。
(6) $l$と$m$が直交するとき、(4)の$S$の最小値を求めよ。また、そのときの$p$の値を求めよ。
福田の数学〜慶應義塾大学2024年経済学部第6問〜3次関数の増減と最大値と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
この動画を見る
$\Large{\boxed{6}}$ $a$,$b$,$p$を実数とする。関数$f(x)$=$x^3$+$ax^2$+$bx$+17 は$x$=$p$で極大値、$x$=$-4p$で極小値をとり、$f(-2p)$=-17 を満たすとする。
(1)$a$,$b$,$p$の値、および$f(x)$の極大値$M$、極大値$m$を、それぞれ求めよ。
(2)(1)で求めた$a$,$b$および0≦$t$≦5 を満たす実数$t$に対して、区間0≦$x$≦$t$ における|$f(x)$|の最大値を$g(t)$とする。$t$の値について場合分けをして、それぞれの場合に$g(t)$を求めよ。
(3)(2)で求めた$g(t)$に対して、定積分$I$=$\displaystyle\int_0^5g(t)dt$ を求めよ。
福田の数学〜九州大学2024年理系第1問〜空間における三角形の面積の最大値
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
この動画を見る
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
福田の数学〜神戸大学2024年理系第2問〜放物線と2接線た作る三角形の重心の軌跡
単元：
#数Ⅱ#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#面積、体積#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$：$y$=$ax^2$+$bx$+$c$
$l_1$：$y$=$-3x$+3
$l_2$：$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
この動画を見る
$\Large\boxed{3}$ $a$, $b$, $c$は実数で、$a$≠0とする。放物線$C$と直線$l_1$, $l_2$をそれぞれ
$C$：$y$=$ax^2$+$bx$+$c$
$l_1$：$y$=$-3x$+3
$l_2$：$y$=$x$+3
で定める。$l_1$, $l_2$がともに$C$と接するとき、以下の問いに答えよ。
(1)$b$を求めよ。$c$を$a$を用いて表せ。
(2)$C$が$x$軸と異なる2点で交わるとき、$\displaystyle\frac{1}{a}$のとりうる値の範囲を求めよ。
(3)$C$と$l_1$の接点をP、$C$と$l_2$の接点をQ、放物線$C$の頂点をRとする。$a$が(2)の条件を満たしながら動くとき、$\triangle PQR$の重心Gの軌跡を求めよ。
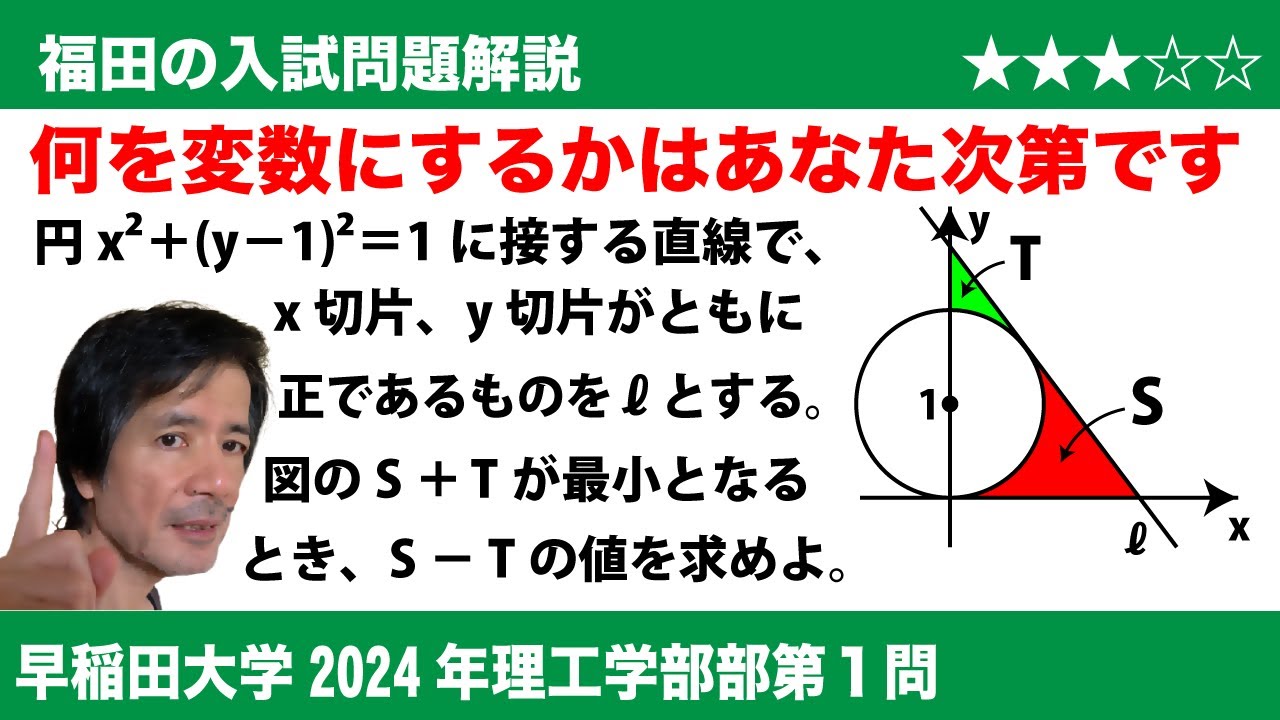
福田の数学〜早稲田大学2024年理工学部第1問〜円の接線で出来る図形の面積の最小
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 円$C$：$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$－$T$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 円$C$：$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$－$T$の値を求めよ。
福田の数学〜早稲田大学2024年人間科学部第4問〜関数の増減と接線の傾きの長さ
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
この動画を見る
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
福田のおもしろ数学126〜条件付き最大値の問題
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の数$x$, $y$が$x^2$－$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
この動画を見る
正の数$x$, $y$が$x^2$－$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。