接線と増減表・最大値・最小値
接線と増減表・最大値・最小値
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
福田の数学〜上智大学2022年TEAP文系型第３問〜３次方程式の解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
aを実数の定数として3次関数
$f(x)=9x^3-9x+a$
を考える。
(1) $y=f(x)$のグラフとx軸の共有点が2つ以上あるようなaの範囲は
$\boxed{ネ}\sqrt{\boxed{ノ}}\leqq a \leqq \boxed{ハ}\sqrt{\boxed{ヒ}}$である。
(2)$a= \boxed{ハ}\sqrt{\boxed{ヒ}}$のとき、方程式$f(x)= 0$の最も小さい解は
$\frac{\boxed{フ}}{\boxed{ヘ}}\sqrt{\boxed{ヒ}}$
であり、$y=f(x)$のグラフとx軸の囲む図形の面積は$\frac{\boxed{マ}}{\boxed{ミ}}$である。
2022上智大学文系過去問
この動画を見る
aを実数の定数として3次関数
$f(x)=9x^3-9x+a$
を考える。
(1) $y=f(x)$のグラフとx軸の共有点が2つ以上あるようなaの範囲は
$\boxed{ネ}\sqrt{\boxed{ノ}}\leqq a \leqq \boxed{ハ}\sqrt{\boxed{ヒ}}$である。
(2)$a= \boxed{ハ}\sqrt{\boxed{ヒ}}$のとき、方程式$f(x)= 0$の最も小さい解は
$\frac{\boxed{フ}}{\boxed{ヘ}}\sqrt{\boxed{ヒ}}$
であり、$y=f(x)$のグラフとx軸の囲む図形の面積は$\frac{\boxed{マ}}{\boxed{ミ}}$である。
2022上智大学文系過去問
東京農工大 ３次関数の最大値
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ f(x)=2x^3-5x^2-4x+1,x \leqq a $における$f(n)$の最大値を求めよ.
東京農工大過去問
この動画を見る
$ f(x)=2x^3-5x^2-4x+1,x \leqq a $における$f(n)$の最大値を求めよ.
東京農工大過去問
福田の数学〜立教大学2022年経済学部第３問〜放物線と円と直線で囲まれた面積
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
福田の数学〜立教大学2022年理学部第３問〜接線法線と囲まれた部分の面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
この動画を見る
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
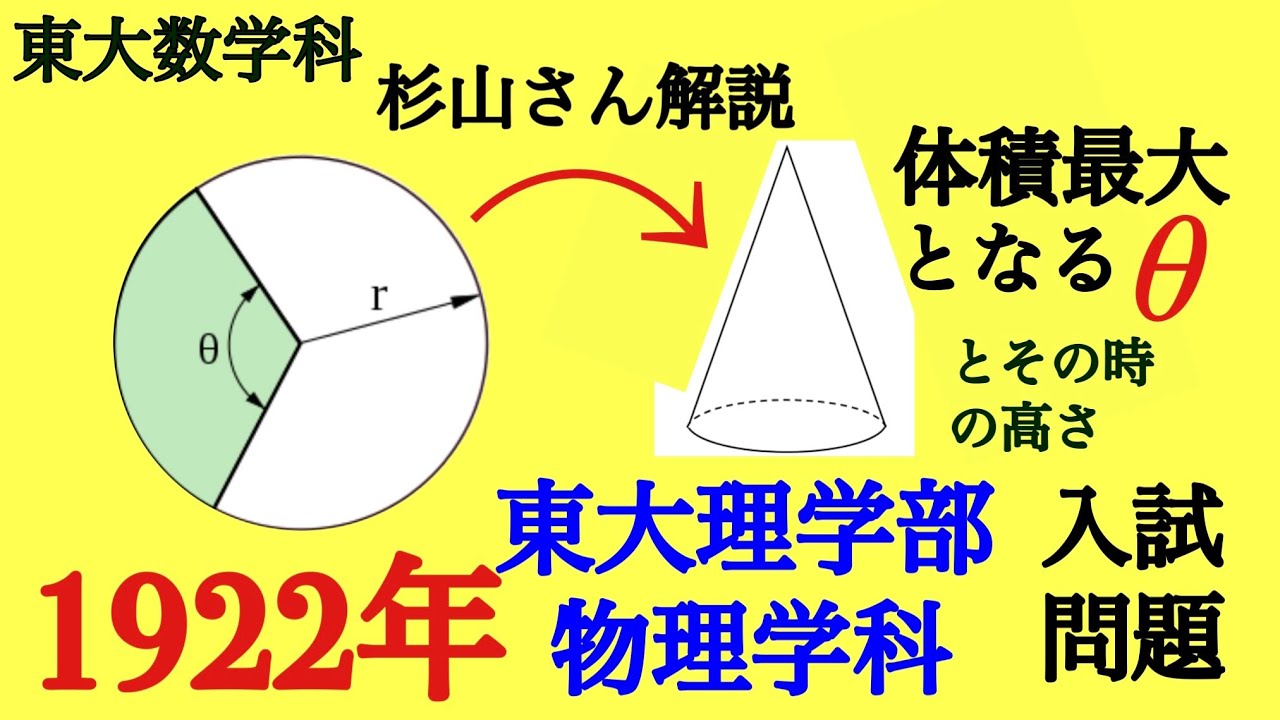
100年前の東大入試問題を東大数学科の杉山さんが解説
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
体積最大となる$\theta$とその時の高さを求めよ.
100年前の東大入試問題に関して解説します.
1922東大理物理学科入試問題
この動画を見る
体積最大となる$\theta$とその時の高さを求めよ.
100年前の東大入試問題に関して解説します.
1922東大理物理学科入試問題
【数Ⅱ】共通接線を求める【2つのグラフが接する・別々の接点をもつ】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$(1)y=ax^2+3x-8,y=x^3+bxがx=2で接するような実数a,bを求めよ.$
$(2)y=x^2+2x+7,y=2x^2の共通接線の方程式を求めよ.$
この動画を見る
$(1)y=ax^2+3x-8,y=x^3+bxがx=2で接するような実数a,bを求めよ.$
$(2)y=x^2+2x+7,y=2x^2の共通接線の方程式を求めよ.$
福田の数学〜明治大学2022年全学部統一入試12AB第２問〜定積分で表された関数と面積の2等分
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
xの関数$f(x)$を$f(x)=x^3$とする。
(1)xの関数$g(x)$を$g(x)=x^3-2x^2-x+3$とする。曲線$y=f(x)$と$y=g(x)$は
3個の交点をもつ。それら交点を$\ x \ $座標が小さい順にA,B,Cとすると、
点$A,B,C$の$\ x\ $座標はそれぞれ$ \boxed{ア},\ \boxed{イ},\ \boxed{ウ}$ である。
曲線$y=g(x)$の接線の傾きが最小となるのは、
接点の$\ x\ $座標が$\frac{\boxed{エ}}{\boxed{オ}}$のときで、
その最小値は$-\frac{\boxed{カ}}{\boxed{\ \ キ\ \ }}$である。
また、点Bを通る$y=g(x)$の接線の傾きの最小値は$-\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(2)$x$ の関数$h(x)$が
$h(x)=-x^2+\frac{x}{6}\int_0^3h(t)dt+4$
を満たすとき、$h(x)=-x^2+\boxed{\ \ コ\ \ }\ x+4$である。
曲線$y=f(x)$と$y=h(x)$の交点の中点は$(\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }})$であり、
$y=f(x)$と$y=h(x)$で囲まれる図形の面積は
原点を通る直線$y=\boxed{\ \ コ\ \ }x$で2等分される。
2022明治大学全統過去問
この動画を見る
xの関数$f(x)$を$f(x)=x^3$とする。
(1)xの関数$g(x)$を$g(x)=x^3-2x^2-x+3$とする。曲線$y=f(x)$と$y=g(x)$は
3個の交点をもつ。それら交点を$\ x \ $座標が小さい順にA,B,Cとすると、
点$A,B,C$の$\ x\ $座標はそれぞれ$ \boxed{ア},\ \boxed{イ},\ \boxed{ウ}$ である。
曲線$y=g(x)$の接線の傾きが最小となるのは、
接点の$\ x\ $座標が$\frac{\boxed{エ}}{\boxed{オ}}$のときで、
その最小値は$-\frac{\boxed{カ}}{\boxed{\ \ キ\ \ }}$である。
また、点Bを通る$y=g(x)$の接線の傾きの最小値は$-\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(2)$x$ の関数$h(x)$が
$h(x)=-x^2+\frac{x}{6}\int_0^3h(t)dt+4$
を満たすとき、$h(x)=-x^2+\boxed{\ \ コ\ \ }\ x+4$である。
曲線$y=f(x)$と$y=h(x)$の交点の中点は$(\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }})$であり、
$y=f(x)$と$y=h(x)$で囲まれる図形の面積は
原点を通る直線$y=\boxed{\ \ コ\ \ }x$で2等分される。
2022明治大学全統過去問
【数Ⅱ】微分とグラフ【増減表で整理しよう。極値を持つ条件、正確に言えますか？】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$(1)y=x^3-6x^2+9x+1のグラフを描け.$
$(2)y=3x^4-8x^3+6x^2のグラフを描け.$
$(3)y=x^3+kx^2+kx+2が極値を持つkの範囲を求めよ.$
この動画を見る
$(1)y=x^3-6x^2+9x+1のグラフを描け.$
$(2)y=3x^4-8x^3+6x^2のグラフを描け.$
$(3)y=x^3+kx^2+kx+2が極値を持つkの範囲を求めよ.$
福田の数学〜早稲田大学2022年社会科学部第２問〜平面幾何と３次関数の増減
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
福田の数学〜早稲田大学2022年商学部第１問(4)〜３次関数のグラフの回転と面積
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{1}}$(4)3次関数f(x)は、x=1で極大値5をとり、x=2で極小値4をとる。
関数$f(x)(x \geqq 0)$のグラフを、原点を中心に時計回りに
θ回転して得られる図形を$C(θ)$とする。
ただし、$0 \lt θ \lt \pi$とする。$C(θ)$と$x$軸の共有点が相異なる3点であるとき、
それらを$x$座標の小さい順に$P_θ,Q_θ,R_θ$とする。線分$Q_θR_θ$と$C(θ)$で
囲まれた部分の面積が$\frac{81}{32}$であるとき、$Q_θ$の$x$座標は$\boxed{\ \ エ\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(4)3次関数f(x)は、x=1で極大値5をとり、x=2で極小値4をとる。
関数$f(x)(x \geqq 0)$のグラフを、原点を中心に時計回りに
θ回転して得られる図形を$C(θ)$とする。
ただし、$0 \lt θ \lt \pi$とする。$C(θ)$と$x$軸の共有点が相異なる3点であるとき、
それらを$x$座標の小さい順に$P_θ,Q_θ,R_θ$とする。線分$Q_θR_θ$と$C(θ)$で
囲まれた部分の面積が$\frac{81}{32}$であるとき、$Q_θ$の$x$座標は$\boxed{\ \ エ\ \ }$である。
2022早稲田大学商学部過去問
三次方程式の解に関するナイスな問題
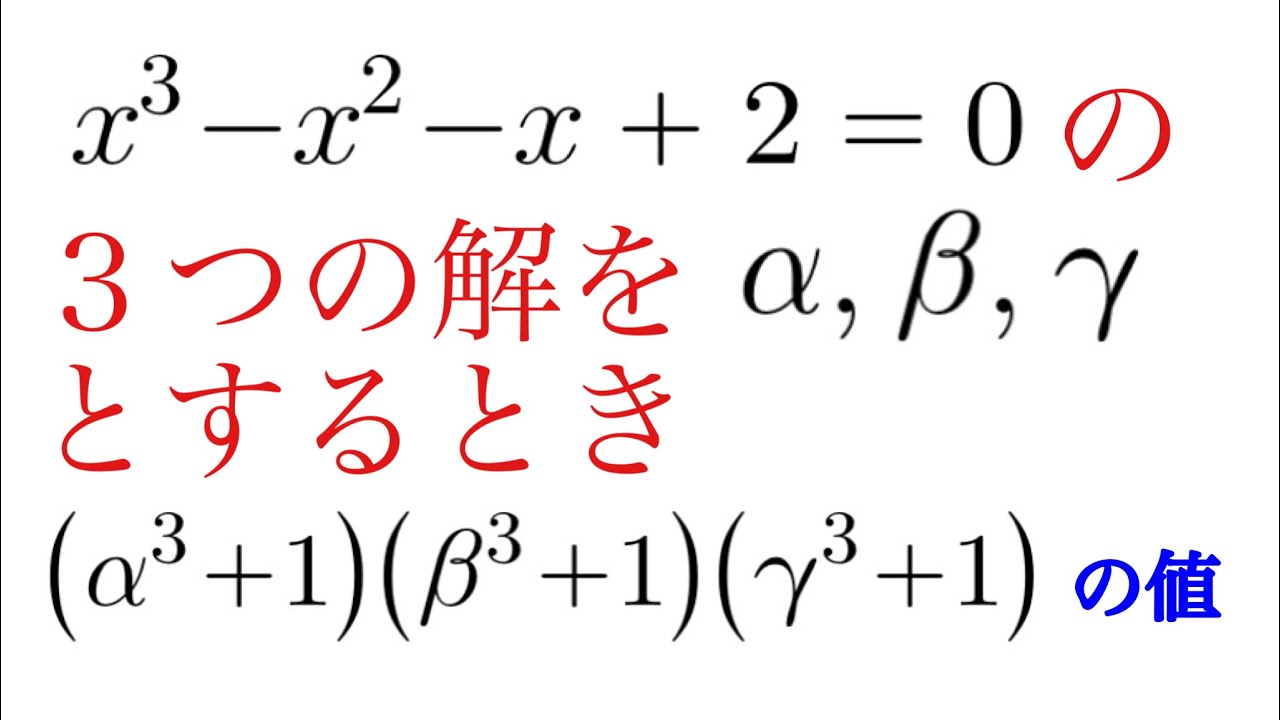
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^3-x^2-x+2=0$の3つの解を$\alpha,\beta,\delta$としたとき,
$(\alpha^3+1)(\beta^3+1)(\delta^3+1)$の値を求めよ.
この動画を見る
$ x^3-x^2-x+2=0$の3つの解を$\alpha,\beta,\delta$としたとき,
$(\alpha^3+1)(\beta^3+1)(\delta^3+1)$の値を求めよ.
【数Ⅱ】微分の定義と接線の方程式【接線の傾きがなんで微分で計算できるのか】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
めいちゃんねる
問題文全文(内容文)：
$(1) y=x^2+2x+3のxが1から3まで変化するときの平均変化率を求めよ.$
$(2)y=x^2+2x+3のx=1における微分係数を求めよ.$
$(3)y=x^2+2x+3上の点(1,6)における接線を求めよ.$
$(4)y=x^2+2x+3のx=aにおける微分係数を求めよ.$
$(5)Y=X^2+2X+3に点(1,2)から引いた接線を求めよ.$
この動画を見る
$(1) y=x^2+2x+3のxが1から3まで変化するときの平均変化率を求めよ.$
$(2)y=x^2+2x+3のx=1における微分係数を求めよ.$
$(3)y=x^2+2x+3上の点(1,6)における接線を求めよ.$
$(4)y=x^2+2x+3のx=aにおける微分係数を求めよ.$
$(5)Y=X^2+2X+3に点(1,2)から引いた接線を求めよ.$
福田の数学〜早稲田大学2022年人間科学部第6問〜楕円を軸以外の直線で回転させた立体の体積
単元：
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#2次曲線#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年人間科学部第４問〜3変数の基本対称式と解と係数の関係
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#複素数#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
福田の数学〜慶應義塾大学2022年看護医療学部第５問〜定積分で表された関数の最小値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{5}}$関数$f(x)$を$f(x)=(x+1)(|x-1|-1)+2$で定める。
(1)$y=f(x)$のグラフをかきなさい。
(2)kを実数とする。このとき、方程式$f(x)=k$が異なる3つの実数解
をもつようなkの値の範囲は$\boxed{\ \ ア\ \ }$である。
(3)曲線$y=f(x)$上の点$P(0,f(0))$における接線lの方程式は$y=\boxed{\ \ イ\ \ }$である。
また、曲線$y=f(x)$と直線lは2つの共有点をもつが、点Pとは異なる共有点を
Qとするとき、点Qのx座標は$\boxed{\ \ ウ\ \ }$である。さらに、曲線$y=f(x)$と直線lで
囲まれた図形の面積は$\boxed{\ \ エ\ \ }$である。
(4)関数$F(x)$を$F(x)=\int_0^xf(t)dt$で定める。このとき、$F'(x)=0$を満たすxを
すべて求めると$x=\boxed{\ \ オ\ \ }$である。これより、関数$F(x)$は
$x=\boxed{\ \ カ\ \ }$で最小値$\boxed{\ \ キ\ \ }$をとることがわかる。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{5}}$関数$f(x)$を$f(x)=(x+1)(|x-1|-1)+2$で定める。
(1)$y=f(x)$のグラフをかきなさい。
(2)kを実数とする。このとき、方程式$f(x)=k$が異なる3つの実数解
をもつようなkの値の範囲は$\boxed{\ \ ア\ \ }$である。
(3)曲線$y=f(x)$上の点$P(0,f(0))$における接線lの方程式は$y=\boxed{\ \ イ\ \ }$である。
また、曲線$y=f(x)$と直線lは2つの共有点をもつが、点Pとは異なる共有点を
Qとするとき、点Qのx座標は$\boxed{\ \ ウ\ \ }$である。さらに、曲線$y=f(x)$と直線lで
囲まれた図形の面積は$\boxed{\ \ エ\ \ }$である。
(4)関数$F(x)$を$F(x)=\int_0^xf(t)dt$で定める。このとき、$F'(x)=0$を満たすxを
すべて求めると$x=\boxed{\ \ オ\ \ }$である。これより、関数$F(x)$は
$x=\boxed{\ \ カ\ \ }$で最小値$\boxed{\ \ キ\ \ }$をとることがわかる。
2022慶應義塾大学看護医療学科過去問
大学入試問題#243 慶應義塾大学(2014) #3次方程式の性質
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k$：実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
この動画を見る
$k$：実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
あの公式が力を発揮する良問！微分・積分のよく出る問題です【数学 入試問題】【九州大学】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
この動画を見る
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
福田の数学〜慶應義塾大学2022年商学部第１問(3)〜放物線の法線
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$(3)放物線上の点Pにおける法線とは、点Pを通り点Pにおける接線に
垂直な直線である。放物線$C_1:y=x^2$上の点$P(a,a^2)$(ただし、$a\neq 0$とする)
における法線の方程式は$y=\boxed{\ \ ア\ \ }$である。
また、実数$p,q$に対し、放物線$C_2:y=-(x-p)^2+q$上のある点における
法線が、放物線$C_1$上の点(1,1)における法線と一致するとき、pとqについて
$q=\boxed{\ \ イ\ \ }$という関係式が成り立つ。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(3)放物線上の点Pにおける法線とは、点Pを通り点Pにおける接線に
垂直な直線である。放物線$C_1:y=x^2$上の点$P(a,a^2)$(ただし、$a\neq 0$とする)
における法線の方程式は$y=\boxed{\ \ ア\ \ }$である。
また、実数$p,q$に対し、放物線$C_2:y=-(x-p)^2+q$上のある点における
法線が、放物線$C_1$上の点(1,1)における法線と一致するとき、pとqについて
$q=\boxed{\ \ イ\ \ }$という関係式が成り立つ。
2022慶應義塾大学商学部過去問
見た目がえぐい問題！実際はシンプルです【数学 入試問題】【大阪大学】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$a$を$0≦a<2\pi$を満たす実数とする。関数
$f(x)=2x^3-(6+3sin a)x^2+(12 sin a)x+sin^3a+6sina+5$について以下の問いに答えよ。
(1)$f(x)$はただ1つの極限値をもつことを示し,その極限値$M(a)$を求めよ。
(2)$0≦a<2\pi$における$M(a)$の最大値とそのときの$a$の値,最小値とそのときの$a$の値をそれぞれ求めよ。
大阪大過去問
この動画を見る
$a$を$0≦a<2\pi$を満たす実数とする。関数
$f(x)=2x^3-(6+3sin a)x^2+(12 sin a)x+sin^3a+6sina+5$について以下の問いに答えよ。
(1)$f(x)$はただ1つの極限値をもつことを示し,その極限値$M(a)$を求めよ。
(2)$0≦a<2\pi$における$M(a)$の最大値とそのときの$a$の値,最小値とそのときの$a$の値をそれぞれ求めよ。
大阪大過去問
こんな問題が京大で出たことあったんだ【数学 入試問題】【京都大学】
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
縦40cm、横25cmの長方形の紙がある。その四隅から、一辺の長さ$x$cmの正方形を切り取り、残りの紙を折りまげて、直方形の形のふたのない容器を作る。
このとき、この箱の容積を$Vcm^3$とする。$V$が最大となる$x$の値を求めよ。
京都大過去問
この動画を見る
縦40cm、横25cmの長方形の紙がある。その四隅から、一辺の長さ$x$cmの正方形を切り取り、残りの紙を折りまげて、直方形の形のふたのない容器を作る。
このとき、この箱の容積を$Vcm^3$とする。$V$が最大となる$x$の値を求めよ。
京都大過去問
微分でもいいけど「あれ」を使えば一瞬です【数学 入試問題】【早稲田大学】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$x>0$のとき、$3x+\dfrac{1}{x^3}$の最小値とそのときの$x$の値を求めよ。
早稲田大過去問
この動画を見る
$x>0$のとき、$3x+\dfrac{1}{x^3}$の最小値とそのときの$x$の値を求めよ。
早稲田大過去問
福田の数学〜筑波大学2022年理系第１問〜円と放物線の接線と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師：
福田次郎
問題文全文(内容文)：
$t,\ p$を実数とし、$t \gt 0$とする。xy平面において、原点Oを中心とし点A(1,t)
を通る円を$C_1$とする。また、点Aにおける$C_1$の接線をlとする。直線$x=p$
を軸とする2次関数のグラフC_2は、x軸と接し、点Aにおいて直線lとも接するとする。
(1)直線$l$の方程式をtを用いて表せ。
(2)pをtを用いて表せ。
(3)$C_2$とx軸の接点をMとし、$C_2$とy軸の交点をNとする。tが正の実数全体を動くとき、
三角形OMNの面積の最小値を求めよ。
2022筑波大学理系過去問
この動画を見る
$t,\ p$を実数とし、$t \gt 0$とする。xy平面において、原点Oを中心とし点A(1,t)
を通る円を$C_1$とする。また、点Aにおける$C_1$の接線をlとする。直線$x=p$
を軸とする2次関数のグラフC_2は、x軸と接し、点Aにおいて直線lとも接するとする。
(1)直線$l$の方程式をtを用いて表せ。
(2)pをtを用いて表せ。
(3)$C_2$とx軸の接点をMとし、$C_2$とy軸の交点をNとする。tが正の実数全体を動くとき、
三角形OMNの面積の最小値を求めよ。
2022筑波大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第３問〜定積分と面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師：
福田次郎
問題文全文(内容文)：
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
曲線$C:y=f(x) (0 \leqq x \lt 1)$が次の条件を満たすとする。
・$f(0)=0$
・$0 \lt x \lt 1$のとき$f'(x) \gt 0$
・$0 \lt a \lt 1$を満たすすべての実数aについて、曲線C上の点$(a, f(a))$
における接線と直線$x=1$との交点をQとするとき、$PQ=1$
この時以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$\int_0^{\frac{1}{2}}(1-x)f'(x)dx$の値を求めよ。
(3)曲線Cとx軸、直線$x=1$、直線$y=f(\frac{1}{2})$で囲まれた部分の面積を求めよ。
2022東京医科歯科大学理系過去問
微分でも解けるけど・・・【数学 入試問題】【慶應義塾大学 改題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。
慶應義塾大改題過去問
この動画を見る
関数$ f(x)=x(x-1)(x-3)(x-4)$の$0≦x≦4$の範囲における最大値と最小値、およびそれらの値を取るときの$x$の値を求めよ。
慶應義塾大改題過去問
福田の数学〜九州大学2022年文系第１問〜絶対値の付いた放物線と直線で囲まれた面積
単元：
#数Ⅱ#大学入試過去問(数学)#２次関数#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
この動画を見る
aを$-3 \lt a \lt 13$を満たす実数とし、次の曲線Cと直線lが接しているとする。
$C:y=|x^2+(3-a)x-3a|, l:y=-x+13$
以下の問いに答えよ。
(1)aの値を求めよ。
(2)曲線Cと直線lで囲まれた2つの図形のうち、点(a,0)が境界線上にある図形の面積を求めよ。
2022九州大学文系過去問
福田の数学〜大阪大学2022年文系第３問〜6分の1公式の証明と面積の最小
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
この動画を見る
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
福田の数学・入試問題解説〜東北大学2022年理系第２問〜4次関数の極値と最小値
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
この動画を見る
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
福田の入試問題解説〜東京大学2022年文系第２問〜3次関数の法施線とグラフとの交点
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$y=x^3-x$により定まる座標平面上の曲線をCとする。
C上の点P$(\alpha,\alpha^3-\alpha)$を通り、
点PにおけるCの接線と垂直に交わる直線をlとする。Cとlは相異なる3点で交わるとする。
(1)$\alpha$のとりうる値の範囲を求めよ。
(2)Cとlの点P以外の2つの交点のx座標を$\beta,\gamma$とする。ただし$\beta \lt \gamma$とする。
$\beta^2+\beta\gamma+\gamma^2-1\neq 0$ となることを示せ。
(3)(2)の$\beta,\gamma$を用いて、
$u=4\alpha^3+\frac{1}{\beta^2+\beta\gamma+\gamma^2-1}$
と定める。このとき、uの取りうる値の範囲を求めよ。
2022東京大学文系過去問
この動画を見る
$y=x^3-x$により定まる座標平面上の曲線をCとする。
C上の点P$(\alpha,\alpha^3-\alpha)$を通り、
点PにおけるCの接線と垂直に交わる直線をlとする。Cとlは相異なる3点で交わるとする。
(1)$\alpha$のとりうる値の範囲を求めよ。
(2)Cとlの点P以外の2つの交点のx座標を$\beta,\gamma$とする。ただし$\beta \lt \gamma$とする。
$\beta^2+\beta\gamma+\gamma^2-1\neq 0$ となることを示せ。
(3)(2)の$\beta,\gamma$を用いて、
$u=4\alpha^3+\frac{1}{\beta^2+\beta\gamma+\gamma^2-1}$
と定める。このとき、uの取りうる値の範囲を求めよ。
2022東京大学文系過去問
福田の数学〜京都大学2022年理系第４問〜四面体に関する証明と線分の長さの最小
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問
この動画を見る
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問