 関数と極限
関数と極限
 関数と極限
関数と極限
福田の数学〜早稲田大学2023年理工学部第3問〜逆関数とで囲まれる面積

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数xに対して関数f(x)をf(x)=$e^{x-2}$で定め、正の実数xに対して関数g(x)をg(x)=$\log x$+2で定める。またy=f(x), y=g(x)のグラフをそれぞれ$C_1$,$C_2$とする。以下の問いに答えよ。
(1)f(x)とg(x)がそれぞれ互いの逆関数であることを示せ。
(2)直線y=xと$C_1$が2点で交わることを示せ。ただし、必要なら2<e<3を証明しないで用いてよい。
(3)直線y=xと$C_1$との2つの交点のx座標を$\alpha$, $\beta$とする。ただし$\alpha$<$\beta$とする。
直線y=xと$C_1$,$C_2$をすべて同じxy平面上に図示せよ。
(4)$C_1$と$C_2$で囲まれる図形の面積を(3)の$\alpha$と$\beta$の多項式で表せ。
2023早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{3}$ 実数xに対して関数f(x)をf(x)=$e^{x-2}$で定め、正の実数xに対して関数g(x)をg(x)=$\log x$+2で定める。またy=f(x), y=g(x)のグラフをそれぞれ$C_1$,$C_2$とする。以下の問いに答えよ。
(1)f(x)とg(x)がそれぞれ互いの逆関数であることを示せ。
(2)直線y=xと$C_1$が2点で交わることを示せ。ただし、必要なら2<e<3を証明しないで用いてよい。
(3)直線y=xと$C_1$との2つの交点のx座標を$\alpha$, $\beta$とする。ただし$\alpha$<$\beta$とする。
直線y=xと$C_1$,$C_2$をすべて同じxy平面上に図示せよ。
(4)$C_1$と$C_2$で囲まれる図形の面積を(3)の$\alpha$と$\beta$の多項式で表せ。
2023早稲田大学理工学部過去問
目で見てわかる収束の値

単元:
#関数と極限#数列の極限#関数の極限#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{4}+\dfrac{1}{4^2}+\dfrac{1}{4^3}+\dfrac{1}{4^4}+・・・・・・+\dfrac{1}{4^n}$
これは収束する値か?
この動画を見る
$\dfrac{1}{4}+\dfrac{1}{4^2}+\dfrac{1}{4^3}+\dfrac{1}{4^4}+・・・・・・+\dfrac{1}{4^n}$
これは収束する値か?
大学入試問題#505「綺麗な数列の問題」 #神戸大学 (2022) #数列 #極限
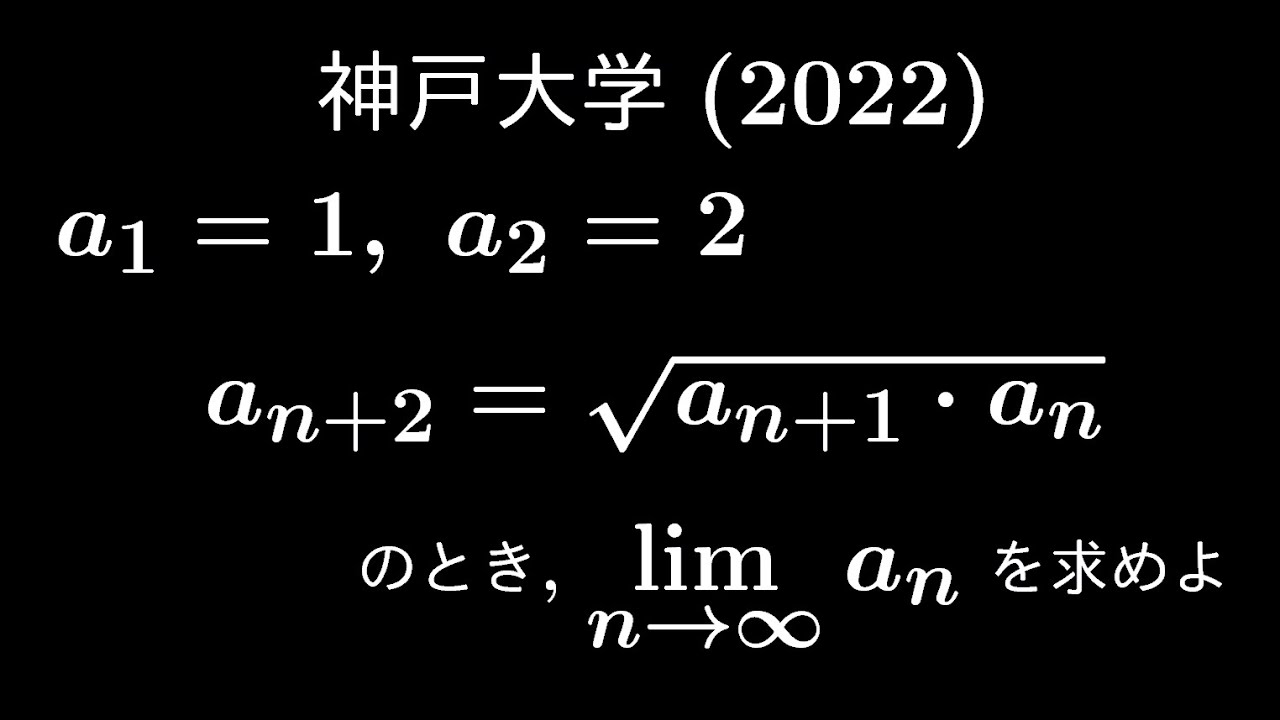
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_{n+1}・a_n }$のとき
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2022年神戸大学 入試問題
【何かを理解!!】極限を解説!

福田の数学〜北海道大学2023年理系第5問〜中間値の定理と関数の増減PART1

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{5}$ a,bを$a^2$+$b^2$<1をみたす正の実数とする。また、座標平面上で原点を中心とする半径1の円をCとし、Cの内部にある2点A(a,0), B(0,b)を考える。
0<θ<$\frac{\pi}{2}$に対してC上の点P($\cos\theta$, $\sin\theta$)を考え、PにおけるCの接線に関してBと対称な点をDとおく。
(1)f(θ)=ab$\cos2\theta$+a$\sin\theta$-b$\cos\theta$とおく。方程式f(θ)=0の解が0<θ<$\frac{\pi}{2}$の範囲に少なくとも1つ存在することを示せ。
(2)Dの座標をa, $\theta$を用いて表せ。
(3)θが0<θ<$\frac{\pi}{2}$の範囲を動くとき、3点A,P,Dが同一直線上にあるようなθは少なくとも1つ存在することを示せ。また、このようなθはただ1つであることを示せ。
2023北海道大学理系過去問
福田の数学〜北海道大学2023年理系第1問〜複素数平面上の図形の列

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
この動画を見る
$\Large\boxed{1}$ 複素数平面上における図形$C_1$, $C_2$, ...,$C_n$, ...は次の条件(A)と(B)を満たすとする。ただし、$i$は虚数単位とする。
(A)$C_1$は原点Oを中心とする半径2の円である。
(B)自然数nに対して、zが$C_n$上を動くとき2w=z+1+$i$で定まるwの描く図形が$C_{n+1}$である。
(1)すべての自然数nに対して、$C_n$は円であることを示し、その中心を表す複素数$\alpha_n$と半径$r_n$を求めよ。
(2)$C_n$上の点とOとの距離の最小値を$d_n$とする。このとき、$d_n$を求めよ。
また、$\displaystyle\lim_{n \to \infty}d_n$を求めよ。
2023北海道大学理系過去問
【0≦θ≦πを問題文に追加】微分すると大変かも・・・ By ~らん~
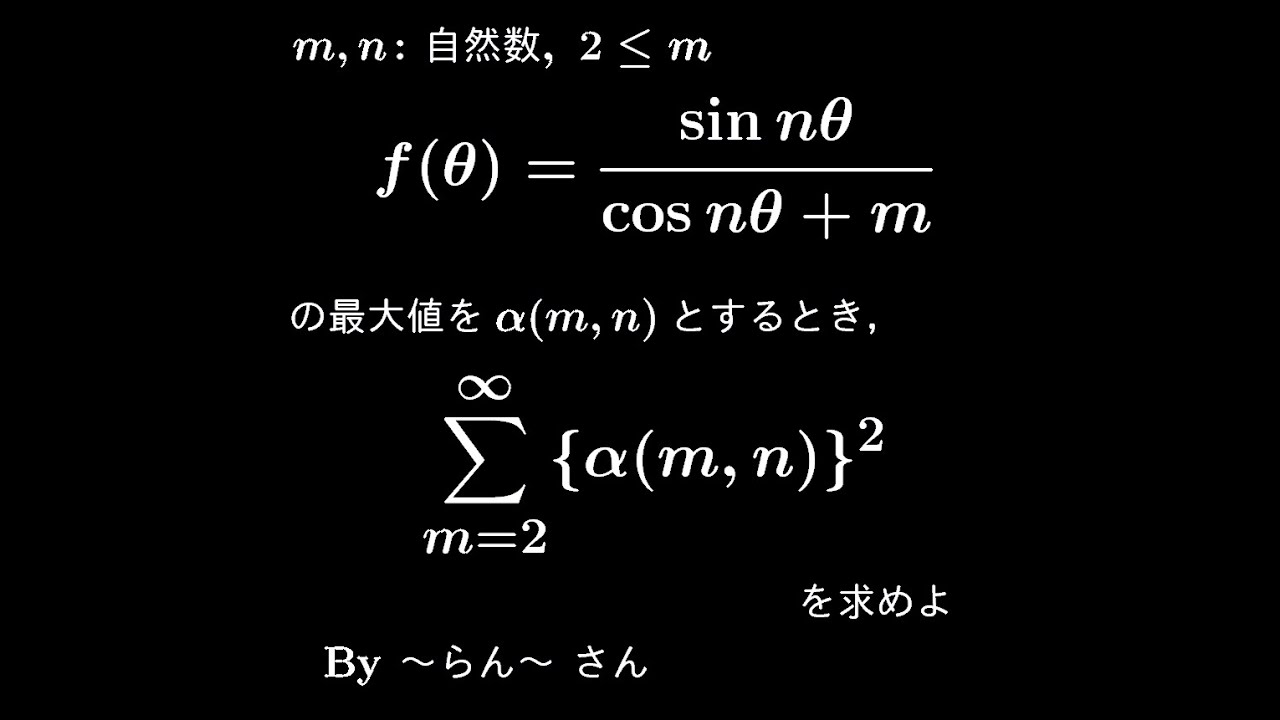
単元:
#数Ⅱ#三角関数#三角関数とグラフ#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
この動画を見る
$m,n$:自然数
$m \geqq 2$
$f(\theta)=\displaystyle \frac{\sin\ n\theta}{\cos\ n\theta+m}$の最大値を$\alpha(m,n)$とする
$\displaystyle \sum_{m=2}^\infty \{\alpha(m,n)\}^2$を求めよ
福田の数学〜大阪大学2023年理系第1問〜不等式の証明と極限

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#微分とその応用#数列の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
この動画を見る
$\Large\boxed{5}$ nを2以上の自然数とする。
(1)0≦x≦1のとき、次の不等式が成り立つことを示せ。
$\frac{1}{2}x^2$≦$\displaystyle(-1)^n\left\{\frac{1}{x+1}-1-\sum\_{k=2}^n(-x)^{k-1}\right\}$≦$x^n-\frac{1}{2}x^{n+1}$
(2)$a_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{k}$ とするとき、次の極限値を求めよ。
$\displaystyle\lim_{n \to \infty}(-1)^nn(a_n-\log 2)$
2023大阪大学理系過去問
大学入試問題#487「みるからに微分」 電気通信大学(2022) #定積分 #極限

単元:
#関数と極限#微分とその応用#積分とその応用#関数の極限#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 4 } \displaystyle \frac{1}{x-4}\displaystyle \int_{2}^{\sqrt{ x }} log(1+t^2)dt$
出典:2022年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 4 } \displaystyle \frac{1}{x-4}\displaystyle \int_{2}^{\sqrt{ x }} log(1+t^2)dt$
出典:2022年電気通信大学 入試問題
【数Ⅲ】極限:無限等比級数の図形への応用問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#サクシード#サクシード数学Ⅲ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
平面上で、点Pが原点Oを出発してx軸方向の正の向きに1だけ進み、次にy軸の正の向きに$\dfrac{3}{4}$だけ進み、次にx軸の負の向きに$\left(\dfrac{3}{4}\right)^2$だけ進み、次にy軸の負の向きに$\left(\dfrac{3}{4}\right)^3$だけ進む。以下、このような運動を限りなく続けるとき、点Pが近付いていく点の座標を求めよ。
この動画を見る
平面上で、点Pが原点Oを出発してx軸方向の正の向きに1だけ進み、次にy軸の正の向きに$\dfrac{3}{4}$だけ進み、次にx軸の負の向きに$\left(\dfrac{3}{4}\right)^2$だけ進み、次にy軸の負の向きに$\left(\dfrac{3}{4}\right)^3$だけ進む。以下、このような運動を限りなく続けるとき、点Pが近付いていく点の座標を求めよ。
【数Ⅲ】極限:無限等比級数で表された関数のグラフの問題

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
教材:
#サクシード#サクシード数学Ⅲ#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$f(x)=\sqrt{x}+\dfrac{\sqrt{x}}{1+\sqrt{x}}+\dfrac{\sqrt{x}}{(1+\sqrt{x})^2}+… $
について$y=f(x)$のグラフを書け
この動画を見る
$f(x)=\sqrt{x}+\dfrac{\sqrt{x}}{1+\sqrt{x}}+\dfrac{\sqrt{x}}{(1+\sqrt{x})^2}+… $
について$y=f(x)$のグラフを書け
大学入試問題#484「なんか不思議な積分」 明治大学2022 #定積分 #極限
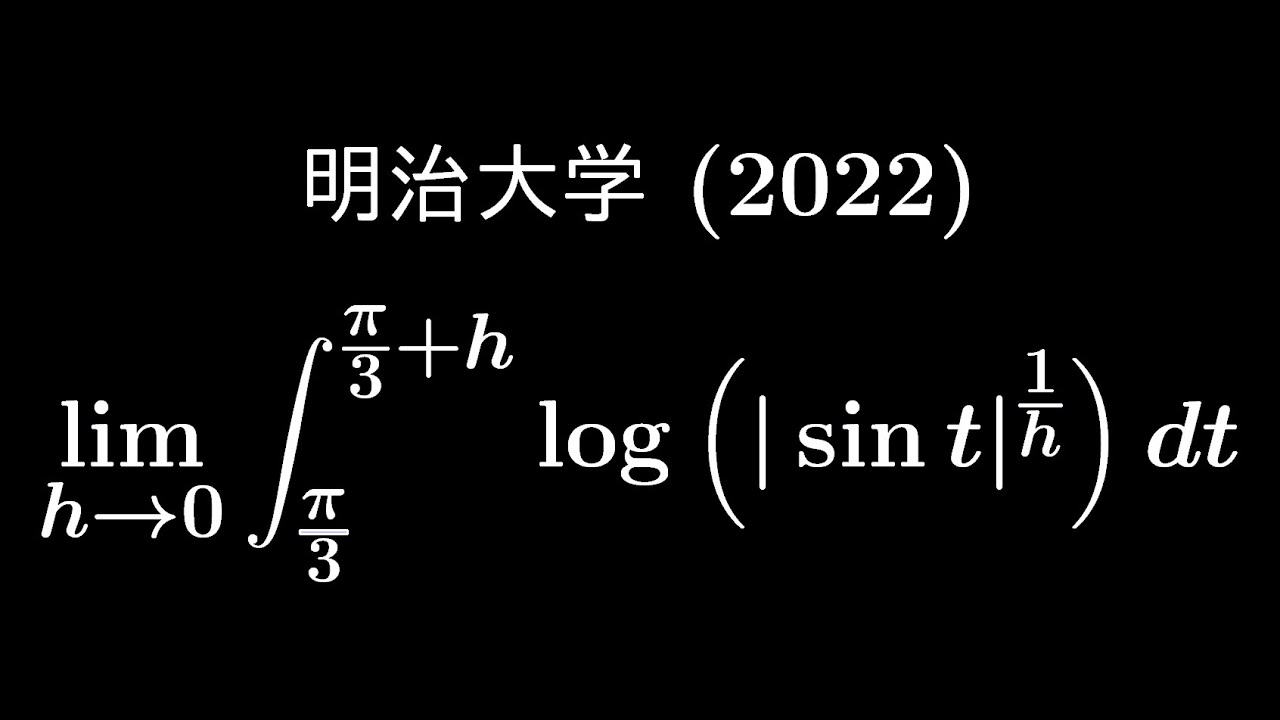
単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ h \to \infty } \displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h} log(|\sin\ t|^{\frac{1}{h}})dt$
出典:2022年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ h \to \infty } \displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h} log(|\sin\ t|^{\frac{1}{h}})dt$
出典:2022年明治大学 入試問題
大学入試問題#477「よくある極限の問題」 藤田医科大学(2023) #極限

単元:
#関数と極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(e^x-1)log(4x+1)}{x^2}$
出典:2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(e^x-1)log(4x+1)}{x^2}$
出典:2023年藤田医科大学 入試問題
福田の数学〜東京慈恵会医科大学2023年医学部第2問〜定積分で表された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
大学入試問題#470「誘導なくてもどうにかできそう」 信州大学 理・医学部(2021) #微積の応用

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
この動画を見る
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
大学入試問題#467「基本すぎる極限問題」 電気通信大学(2013) #極限

単元:
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{(1-\cos2x)\sin3x}{x^3}$
出典:2013年電気通信大学 入試問題
大学入試問題#466「絶対に知っておくべき解き方」 電気通信大学(2014) #極限

単元:
#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 1 } \displaystyle \frac{x^2log(x+1)-log\ 2}{x-1}$
出典:2014年電気通信大学 入試問題
大学入試問題#465「よくある極限問題」 電気通信大学2009 #極限

単元:
#大学入試過去問(数学)#三角関数#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin2x-2\sin\ x}{x\ \sin^2\ x}$
出典:2009年電気通信大学 入試問題
極限の難問!答えは予測できるが・・・【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
この動画を見る
$\displaystyle \lim_{ x \to \infty }(\cos^2 \sqrt{x+1}+\sin^2\sqrt{x})$を求めよ。
一橋大過去問
福田の1.5倍速演習〜合格する重要問題090〜名古屋大学2018年度理系第1問〜定積分と不等式と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
大学入試問題#459「構想力が問われる問題」 早稲田大学(2017) #連続関数

単元:
#大学入試過去問(数学)#関数と極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$C$:定数 $-1 \lt C \lt 1$
すべての実数$x$に対して
$f(x)+f(cx)=x^2$を満たす連続関数$f(x)$を求めよ
出典:2017年早稲田大学 入試問題
この動画を見る
$C$:定数 $-1 \lt C \lt 1$
すべての実数$x$に対して
$f(x)+f(cx)=x^2$を満たす連続関数$f(x)$を求めよ
出典:2017年早稲田大学 入試問題
大学入試問題#457「いかにしてサッパリ解くか!」 横浜国立大学(2001) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{dx}{x\sqrt{ 1+x^3 }}$
出典:2001年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{dx}{x\sqrt{ 1+x^3 }}$
出典:2001年横浜国立大学 入試問題
大学入試問題#455「落とすと落ちる問題② 横浜国立大学 後期 (2003) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{16} \displaystyle \frac{dx}{\sqrt{ x }+\sqrt[ 4 ]{ x }}$
出典:2003年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{16} \displaystyle \frac{dx}{\sqrt{ x }+\sqrt[ 4 ]{ x }}$
出典:2003年横浜国立大学 入試問題
大学入試問題#454「落とすと落ちる問題①」 横浜国立大学 後期 2003 #定積分

単元:
#大学入試過去問(数学)#三角関数#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}} \displaystyle \frac{dx}{\sin\ x+\sqrt{ 3 }\ \cos\ x}$
出典:2003年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} \displaystyle \frac{dx}{\sin\ x+\sqrt{ 3 }\ \cos\ x}$
出典:2003年横浜国立大学 入試問題
東京医科大学 対数の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=(1+x)\log(3+x)-(1+x)\log(5+x)$
$\displaystyle \lim_{ n \to \infty } f(x) =?$
東京医科大過去問
この動画を見る
$f(x)=(1+x)\log(3+x)-(1+x)\log(5+x)$
$\displaystyle \lim_{ n \to \infty } f(x) =?$
東京医科大過去問
ハルハルさんの積分問題(準備) 難易度高めの最後まで気が抜けない!!
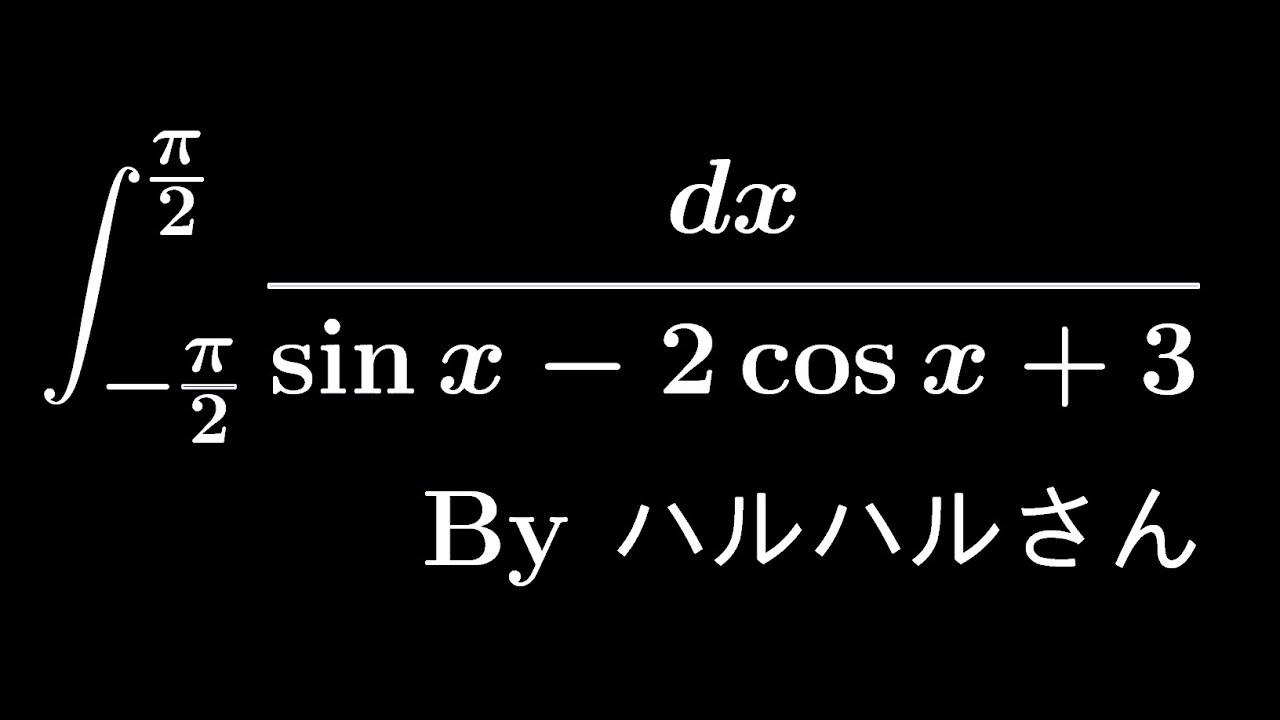
単元:
#三角関数#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$K=\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{dx}{\sin\ x-2\cos\ x+3}$
この動画を見る
$K=\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{dx}{\sin\ x-2\cos\ x+3}$
福田の1.5倍速演習〜合格する重要問題080〜京都大学2018年度理系第5問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
この動画を見る
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
大学入試問題#453「落とせない問題」 信州大学(2022) #定積分

単元:
#大学入試過去問(数学)#対数関数#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{dx}{x(1+log\ x^3)log\ x}$
出典:2022年信州大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^2} \displaystyle \frac{dx}{x(1+log\ x^3)log\ x}$
出典:2022年信州大学 入試問題
福田の1.5倍速演習〜合格する重要問題077〜東京大学2018年度理系第3問〜ベクトル方程式の表す点の存在範囲と面積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#ベクトルと平面図形、ベクトル方程式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#面積、体積#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
第3問
放物線y=$x^2$のうち-1≦x≦1を満たす部分をCとする。
座標平面上の原点Oと点A(1,0)を考える。k>0を実数とする。点PがC上を動き、点Qが線分OA上を動くとき
$\overrightarrow{OR}$=$\frac{1}{k}\overrightarrow{OP}$+$k\overrightarrow{OQ}$
を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle\lim_{k \to +0}S(k)$, $\displaystyle\lim_{k \to \infty}S(k)$を求めよ。
2018東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題075〜浜松医科大学2017年度医学部第1問〜複素数の実部と虚部

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
この動画を見る
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
