 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学135〜ガウス記号のついた方程式の解

福田の数学〜早稲田大学2024年理工学部第2問〜重複順列と連立漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を自然数とし、数1, 2, 4を重複を許して$n$個並べてできる$n$桁の自然数全体を考える。そのうちで3の倍数となるものの個数を$a_n$、3で割ると1余るものの個数を$b_n$、3で割ると2余るものの個数を$c_n$とする。
(1)$a_{n+1}$を$b_n$, $c_n$を用いて表せ。同様に$b_{n+1}$を$a_n$, $c_n$を用いて、$c_{n+1}$を$a_n$, $b_n$を用いて表せ。
(2)$a_{n+2}$を$n$と$c_n$を用いて表せ。
(3)$a_{n+6}$を$n$と$a_n$を用いて表せ。
(4)$a_{6m+1} (m=0,1,2,...)$を$m$を用いて表せ。
この動画を見る
$\Large\boxed{2}$ $n$を自然数とし、数1, 2, 4を重複を許して$n$個並べてできる$n$桁の自然数全体を考える。そのうちで3の倍数となるものの個数を$a_n$、3で割ると1余るものの個数を$b_n$、3で割ると2余るものの個数を$c_n$とする。
(1)$a_{n+1}$を$b_n$, $c_n$を用いて表せ。同様に$b_{n+1}$を$a_n$, $c_n$を用いて、$c_{n+1}$を$a_n$, $b_n$を用いて表せ。
(2)$a_{n+2}$を$n$と$c_n$を用いて表せ。
(3)$a_{n+6}$を$n$と$a_n$を用いて表せ。
(4)$a_{6m+1} (m=0,1,2,...)$を$m$を用いて表せ。
福田の中学入試の算数002〜ラサール中学校2005年〜ベンチの数と生徒の数

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
福田次郎
問題文全文(内容文):
生徒を5人ずつベンチに座らせたところ、ベンチが2つ足りないことがわかりました。そこで、座れなかった生徒を1つずつ、5人ずつ座っているベンチに座らせていきました。すると、(5人ずつ座っているベンチの数):(6人ずつ座っているベンチの数)=5:4になりました。生徒は何人いますか。
この動画を見る
生徒を5人ずつベンチに座らせたところ、ベンチが2つ足りないことがわかりました。そこで、座れなかった生徒を1つずつ、5人ずつ座っているベンチに座らせていきました。すると、(5人ずつ座っているベンチの数):(6人ずつ座っているベンチの数)=5:4になりました。生徒は何人いますか。
福田の数学〜早稲田大学2024年理工学部第1問〜円の接線で出来る図形の面積の最小
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
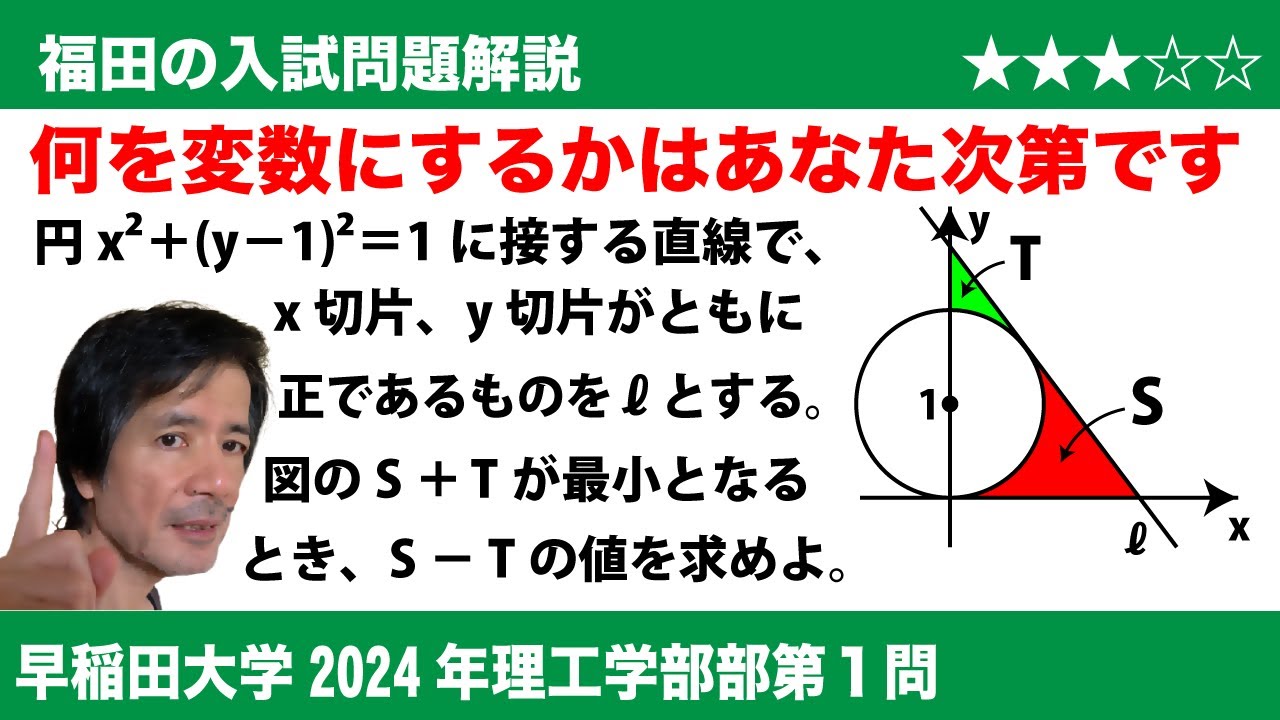
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 円$C$:$x^2$+$(y-1)^2$=1 に接する直線で、$x$切片、$y$切片がともに正であるものを$l$とする。$C$と$l$と$x$軸により囲まれた部分の面積を$S$、$C$と$l$と$y$軸により囲まれた部分の面積を$T$とする。$S$+$T$が最小となるとき、$S$-$T$の値を求めよ。
福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面
単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
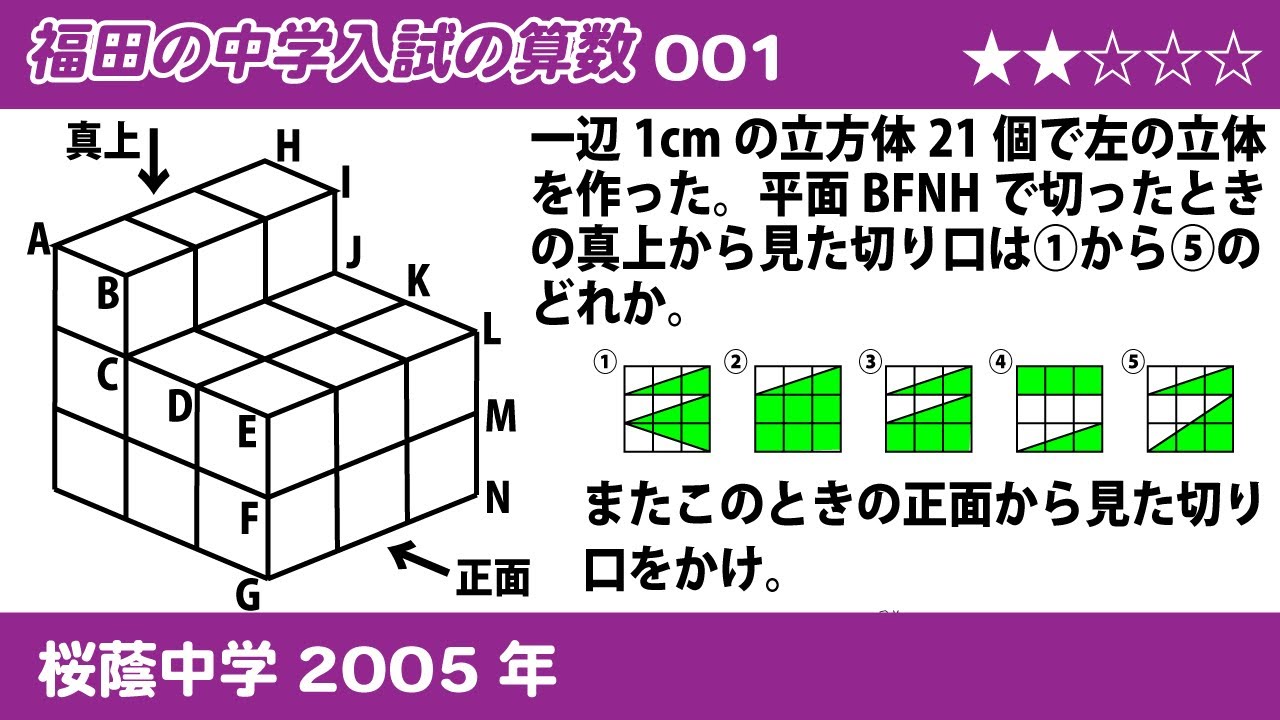
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
この動画を見る
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
福田の数学〜早稲田大学2024年人間科学部第7問〜内サイクロイド曲線の長さ
単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
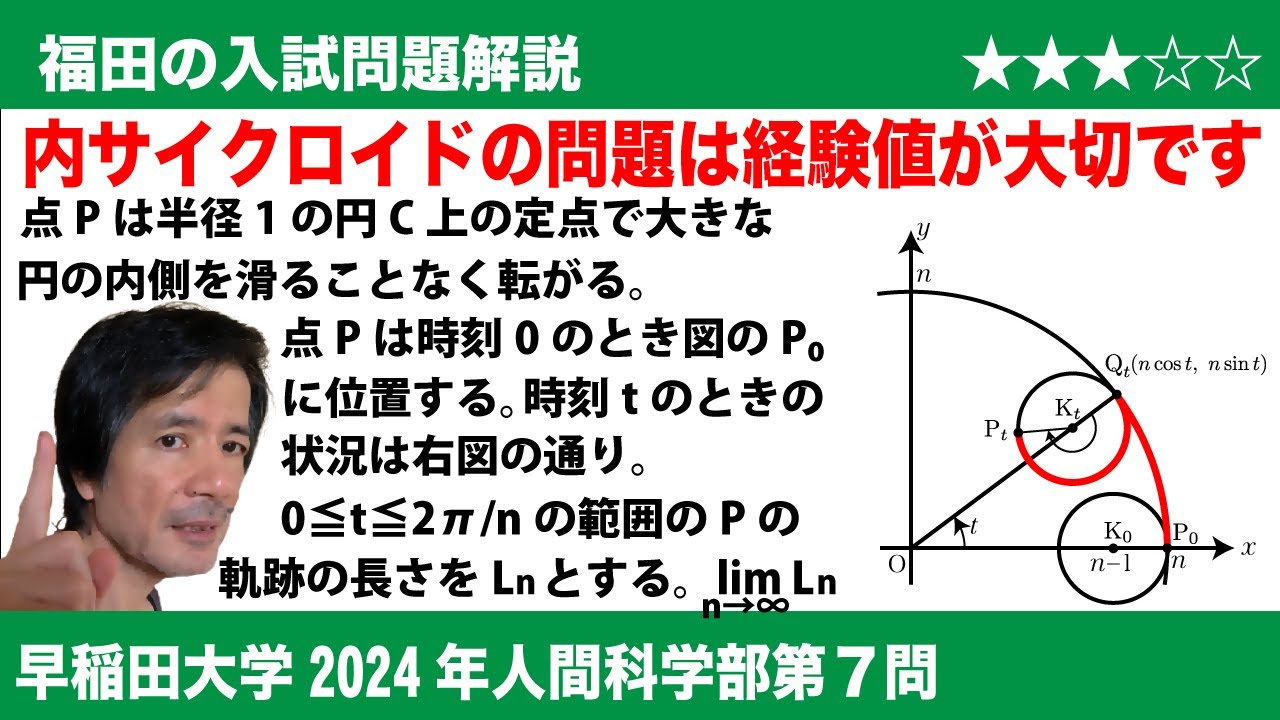
$\Large\boxed{7}$ $n$を2以上の自然数とする。座標平面において、原点を中心とする半径$n$の円$C_n$の内側を半径1の円$C$が滑らずに転がるとき、円$C$上の定点Pの軌跡について考える。時刻$t$において、2つの円$C$と$C_n$は点($n\cos t$, $n\sin t$)で接している。
また、時刻$t$=0 において、点Pは点($n$, 0)にある。$t$が0≦$t$≦$\displaystyle\frac{2\pi}{n}$ の範囲を動くとき、点Pの軌跡の長さを$L_n$とする。このとき、$L_2$=$\boxed{\ \ テ\ \ }$である。また、$\displaystyle\lim_{n \to \infty}L_n$=$\boxed{\ \ ト\ \ }$である。
この動画を見る
$\Large\boxed{7}$ $n$を2以上の自然数とする。座標平面において、原点を中心とする半径$n$の円$C_n$の内側を半径1の円$C$が滑らずに転がるとき、円$C$上の定点Pの軌跡について考える。時刻$t$において、2つの円$C$と$C_n$は点($n\cos t$, $n\sin t$)で接している。
また、時刻$t$=0 において、点Pは点($n$, 0)にある。$t$が0≦$t$≦$\displaystyle\frac{2\pi}{n}$ の範囲を動くとき、点Pの軌跡の長さを$L_n$とする。このとき、$L_2$=$\boxed{\ \ テ\ \ }$である。また、$\displaystyle\lim_{n \to \infty}L_n$=$\boxed{\ \ ト\ \ }$である。
福田のおもしろ数学134〜n個の因数の席の計算

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
福田次郎
問題文全文(内容文):
次の式を計算せよ。$x$≠1 とする。
(1+$x$)(1+$x^2$)(1+$x^4$)...(1+$x^{2^{n-1}}$) を計算せよ。
この動画を見る
次の式を計算せよ。$x$≠1 とする。
(1+$x$)(1+$x^2$)(1+$x^4$)...(1+$x^{2^{n-1}}$) を計算せよ。
福田の数学〜早稲田大学2024年人間科学部第6問〜空間内の折れ線の長さの最小値
単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
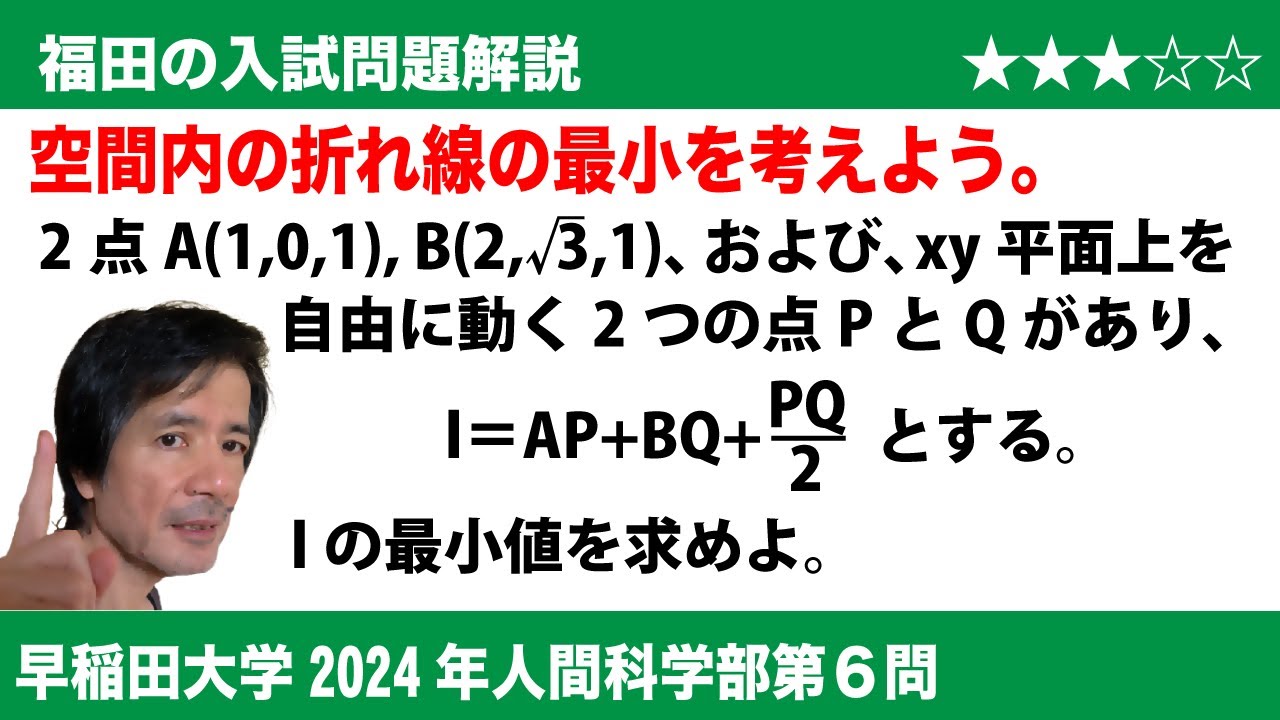
$\Large\boxed{6}$ 2点A(1,0,1)とB(2, $\sqrt 3$, 1)、および、$xy$平面上を自由に動く2つの点PとQがあり、$l$=AP+BQ+$\displaystyle\frac{\textrm{PQ}}{2}$とする。$l$が最小値をとるとき、点PとQを通る$xy$平面上の直線の方程式は$y$=$\sqrt{\boxed{\ \ ソ\ \ }\ x}$-$\sqrt{\boxed{\ \ タ\ \ }}$ であり、$l$の最小値は$\boxed{\ \ チ\ \ }$+$\sqrt{\boxed{\ \ ツ\ \ }}$ である。
この動画を見る
$\Large\boxed{6}$ 2点A(1,0,1)とB(2, $\sqrt 3$, 1)、および、$xy$平面上を自由に動く2つの点PとQがあり、$l$=AP+BQ+$\displaystyle\frac{\textrm{PQ}}{2}$とする。$l$が最小値をとるとき、点PとQを通る$xy$平面上の直線の方程式は$y$=$\sqrt{\boxed{\ \ ソ\ \ }\ x}$-$\sqrt{\boxed{\ \ タ\ \ }}$ であり、$l$の最小値は$\boxed{\ \ チ\ \ }$+$\sqrt{\boxed{\ \ ツ\ \ }}$ である。
福田のおもしろ数学133〜命題の否定〜夏は暑い

福田の数学〜早稲田大学2024年人間科学部第5問〜円の性質と切り取られる弦の長さ

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 2点A(-$\sqrt 2$-$\sqrt 6$, $\sqrt 2$-$\sqrt 6$), B($\sqrt 2$+$\sqrt 6$, $\sqrt 2$-$\sqrt 6$)と原点O(0, 0)について、$\theta$=$\angle\textrm{AOB}$ とするとき、$\theta$=$\displaystyle\frac{\boxed{ナ}}{\boxed{ニ}}\pi$ である。ただし、0≦$\theta$≦$\pi$ とする。さらに円$x^2$+$y^2$-$2x$-$10y$+22=0 を$C$とする。円$C$上の点P, Qは
$\angle\textrm{APB}$=$\angle\textrm{AQB}$=$\displaystyle\frac{5}{12}\pi$
を満たす点とする。このとき、PQ=$\displaystyle\boxed{ヌ}\sqrt{\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}}$ である。
この動画を見る
$\Large\boxed{5}$ 2点A(-$\sqrt 2$-$\sqrt 6$, $\sqrt 2$-$\sqrt 6$), B($\sqrt 2$+$\sqrt 6$, $\sqrt 2$-$\sqrt 6$)と原点O(0, 0)について、$\theta$=$\angle\textrm{AOB}$ とするとき、$\theta$=$\displaystyle\frac{\boxed{ナ}}{\boxed{ニ}}\pi$ である。ただし、0≦$\theta$≦$\pi$ とする。さらに円$x^2$+$y^2$-$2x$-$10y$+22=0 を$C$とする。円$C$上の点P, Qは
$\angle\textrm{APB}$=$\angle\textrm{AQB}$=$\displaystyle\frac{5}{12}\pi$
を満たす点とする。このとき、PQ=$\displaystyle\boxed{ヌ}\sqrt{\frac{\boxed{\ \ ネ\ \ }}{\boxed{\ \ ノ\ \ }}}$ である。
福田のおもしろ数学132〜合成関数のグラフ

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
この動画を見る
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
福田の数学〜早稲田大学2024年人間科学部第4問〜関数の増減と接線の傾きの長さ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
この動画を見る
$\Large\boxed{4}$ $f(x)$=$x^3$+$ax^2$+$bx$+$\displaystyle\frac{1}{4}a^2$ が$x$=-2 で極値をとり、その値が1であるとき、定数$a$, $b$の値は$a$=$\boxed{\ \ ソ\ \ }$, $b$=$\boxed{\ \ タ\ \ }$ である。このとき、曲線$y$=$f(x)$上の点$(t, f(t))$における接線の傾きは$t$=$\displaystyle\frac{\boxed{チ}}{\boxed{ツ}}$ のとき、最小値$\displaystyle\frac{\boxed{テ}}{\boxed{ト}}$ をとる。
福田のおもしろ数学131〜直角三角形どうしの重なった部分の面積
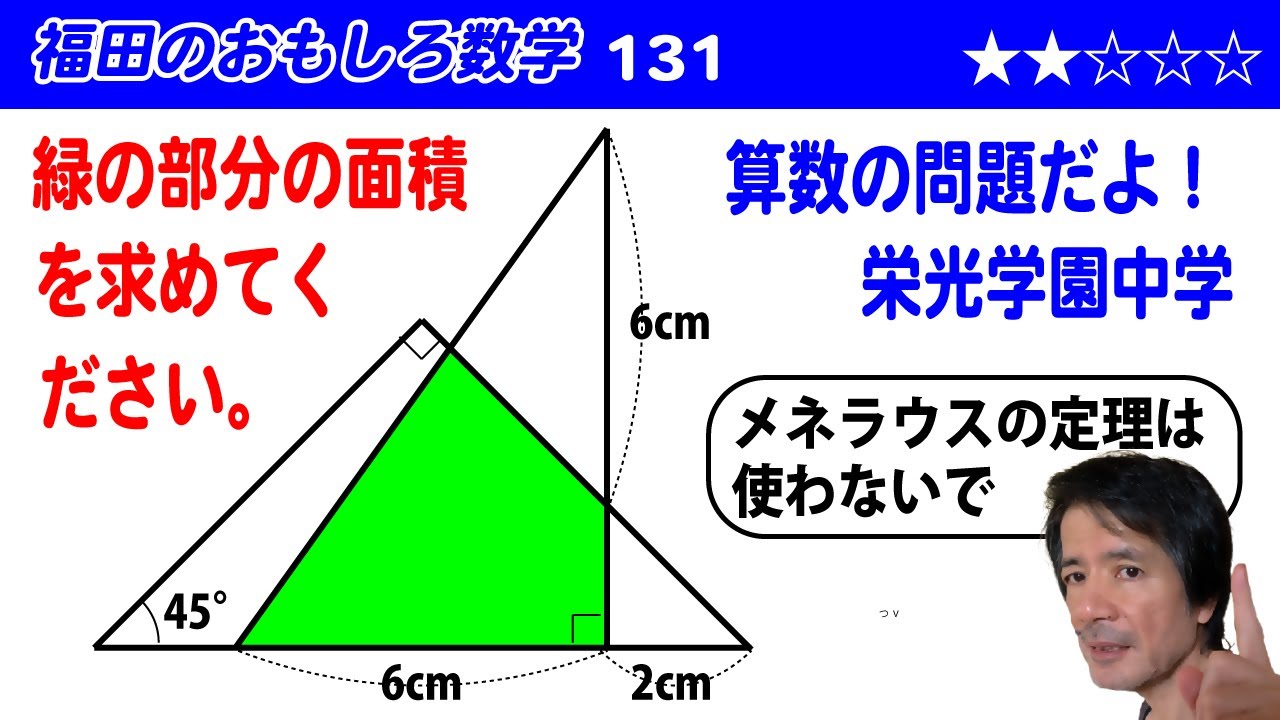
福田の数学〜早稲田大学2024年人間科学部第3問〜平面へ下ろした垂線の長さ
単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 直方体OABC-DEFGにおける各辺の長さは
OA=CB=DE=GF=1
AB=OC=EF=DG=$\sqrt 2$
OD=AE=BF=CG=$\sqrt 3$
である。点Bから3点O, E, Gを含む平面に下ろした垂線の足をHとする。このとき、$\overrightarrow{\textrm{OH}}$=$\displaystyle\frac{\boxed{ケ}}{\boxed{コ}}\overrightarrow{\textrm{OE}}$+$\displaystyle\frac{\boxed{サ}}{\boxed{シ}}\overrightarrow{\textrm{OG}}$ と表すことができ、$|\overrightarrow{\textrm{BH}}|^2$=$\displaystyle\frac{\boxed{ス}}{\boxed{セ}}$ である。
この動画を見る
$\Large\boxed{3}$ 直方体OABC-DEFGにおける各辺の長さは
OA=CB=DE=GF=1
AB=OC=EF=DG=$\sqrt 2$
OD=AE=BF=CG=$\sqrt 3$
である。点Bから3点O, E, Gを含む平面に下ろした垂線の足をHとする。このとき、$\overrightarrow{\textrm{OH}}$=$\displaystyle\frac{\boxed{ケ}}{\boxed{コ}}\overrightarrow{\textrm{OE}}$+$\displaystyle\frac{\boxed{サ}}{\boxed{シ}}\overrightarrow{\textrm{OG}}$ と表すことができ、$|\overrightarrow{\textrm{BH}}|^2$=$\displaystyle\frac{\boxed{ス}}{\boxed{セ}}$ である。
福田のおもしろ数学130〜合成関数の性質

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
この動画を見る
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
福田の数学〜早稲田大学2024年人間科学部第2問〜反復試行と条件付き確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$-1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
この動画を見る
$\Large\boxed{2}$ $n$を2以上の自然数とする。1から$n$までの番号が1つずつつけられた$n$個の玉が中身の見えない袋に入っている。袋の中から1個の玉を選んで番号を確認して袋に戻すという操作を$n$回繰り返す。この$n$回の操作の中で、1から$n$-1までのいずれの番号の玉も選ばれているとき、番号が$n$の玉も選ばれている条件付き確率を$P(n)$とするとき、$P(3)$=$\frac{\boxed{オ}}{\boxed{カ}}$, $P(50)$=$\frac{\boxed{キ}}{\boxed{ク}}$ である。
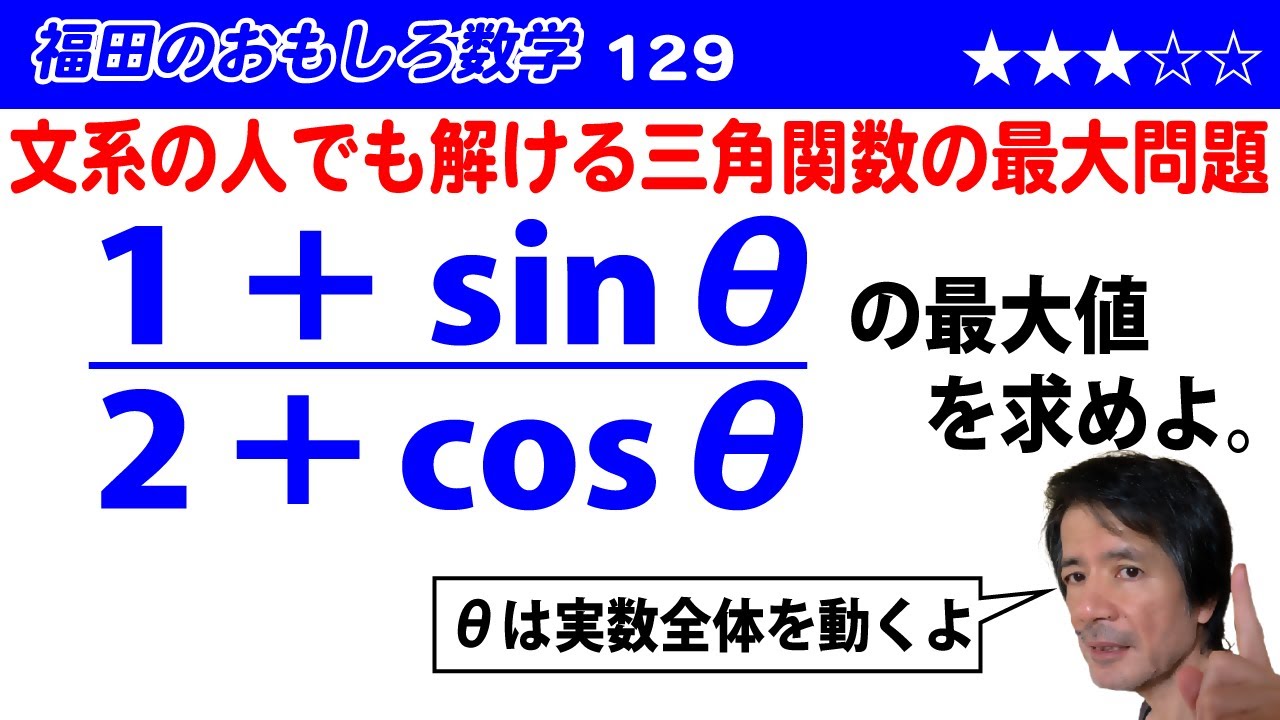
福田のおもしろ数学129〜三角関数の最大問題
単元:
#数Ⅱ#三角関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
この動画を見る
$\displaystyle\frac{1+\sin\theta}{2+\cos\theta}$($\theta$は実数)の最大値を求めよ。
福田の数学〜早稲田大学2024年人間科学部第1問(3)〜指数法則と式の値

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
この動画を見る
$\Large\boxed{1}$ (3)$10^x$=25, $100^y$=400 のとき、$3x$+$6y$-2=$\boxed{エ}$ である。
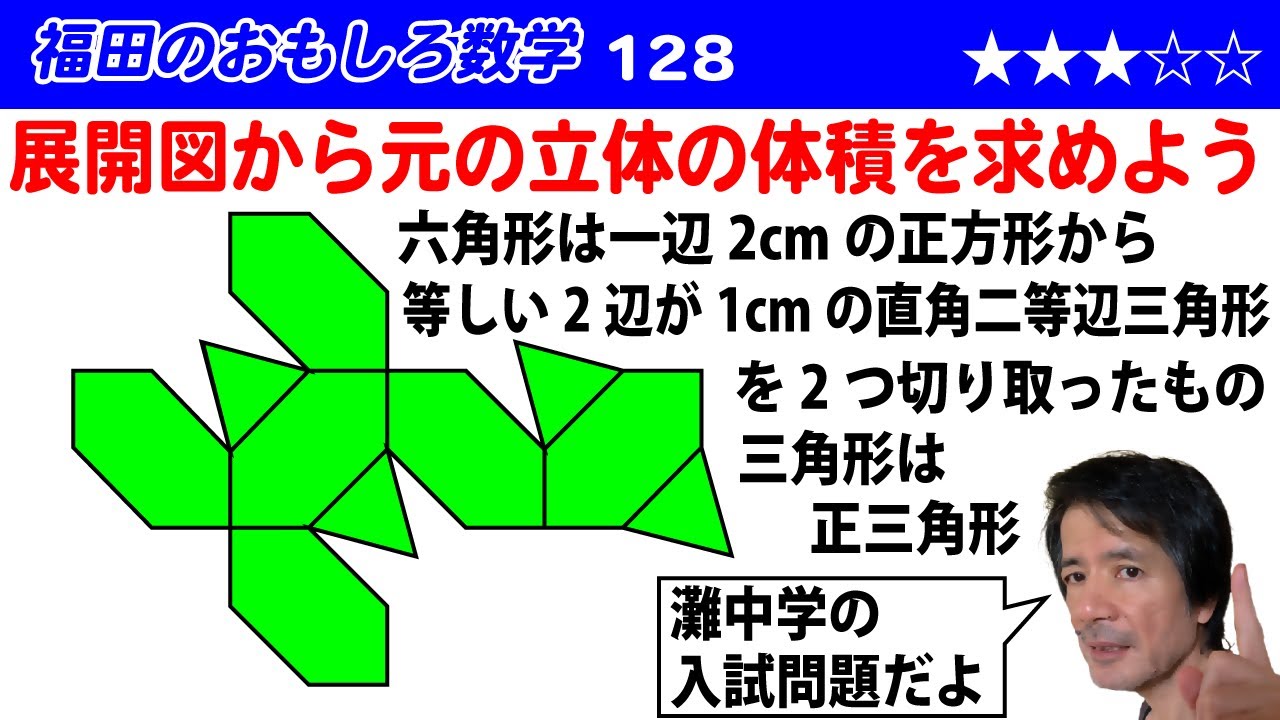
福田のおもしろ数学128〜灘中学の問題〜展開図から元の立体の体積を求める
福田の数学〜早稲田大学2024年人間科学部第1問(2)〜不等式の表す領域の面積

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
この動画を見る
$\Large\boxed{1}$ (2)次の連立不等式で表される領域の面積は$\boxed{イ}$+$\boxed{ウ}\pi$ である。
$\left\{\begin{array}{1}
x^2+y^2≦4|x|+4|y|\\
x^2≦y^2\\
\end{array}\right.$
福田のおもしろ数学127〜こんな漸化式解けるの?〜難しい漸化式の解き方

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
この動画を見る
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
福田の数学〜早稲田大学2024年人間科学部第1問(1)〜4次式の最小値

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$x$が実数であるとき、$x(x+1)(x+2)(x+3)$ の最小値は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)$x$が実数であるとき、$x(x+1)(x+2)(x+3)$ の最小値は$\boxed{\ \ ア\ \ }$である。
福田のおもしろ数学126〜条件付き最大値の問題

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
この動画を見る
正の数$x$, $y$が$x^2$-$2x$+$4y^2$=0 を満たして変わるとき、$xy$の最大値を求めよ。
福田の数学〜一橋大学2024年文系第5問〜円の中心を含む三角形になる確率
単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
この動画を見る
$\Large\boxed{5}$ $n$を3以上の奇数とする。円に内接する正$n$角形の頂点から無作為に相異なる3点を選んだ時、その3点を頂点とする三角形の内部に円の中心が含まれる確率$p_n$を求めよ。
福田のおもしろ数学125〜池の周りを回る3人の速さ

単元:
#算数(中学受験)#過去問解説(学校別)#速さ#旅人算・通過算・流水算#麻布中学
指導講師:
福田次郎
問題文全文(内容文):
池の周りをA君とB君は同じ方向に、C君は逆方向に、それぞれ一定の速さで周ります。A君はB君を15分ごとに追い越し、B君はC君と2分ごとに出会います。B君が7分かかって走る距離をC君は8分で走ります。このとき、A君とC君の速さの比を求めなさい。
この動画を見る
池の周りをA君とB君は同じ方向に、C君は逆方向に、それぞれ一定の速さで周ります。A君はB君を15分ごとに追い越し、B君はC君と2分ごとに出会います。B君が7分かかって走る距離をC君は8分で走ります。このとき、A君とC君の速さの比を求めなさい。
福田の数学〜一橋大学2024年文系第4問〜ひし形になる条件と面積の最小

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{4}$ 実数$a$,$b$は-1<$a$<1, -1<$b$<1 を満たす。座標空間内に4点A($a$, -1, -1), B(-1, $b$, -1), C($-a$, 1, 1), D(1, $-b$, 1)をとる。
(1)A, B, C, Dがひし形の頂点となるとき、$a$と$b$の会計を表す等式を求めよ。
(2)$a$, $b$が(1)の等式を満たすとき、A, B, C, Dを頂点とする四角形の面積の最小値を求めよ。
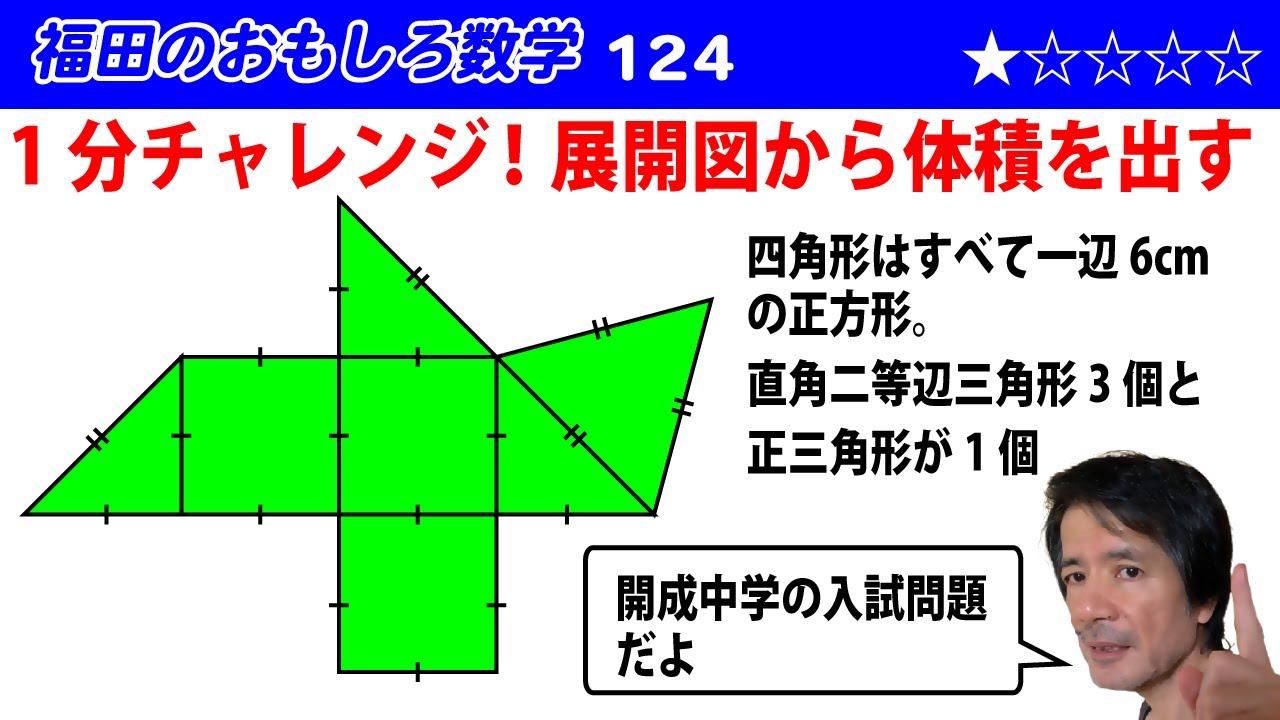
福田のおもしろ数学124〜展開図から立体の体積を求める
福田の数学〜一橋大学2024年文系第3問〜多項式の商と余り

単元:
#数Ⅱ#剰余の定理・因数定理・組み立て除法と高次方程式#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
福田のおもしろ数学123〜どうして積分すると面積が求まるのでしょう?
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
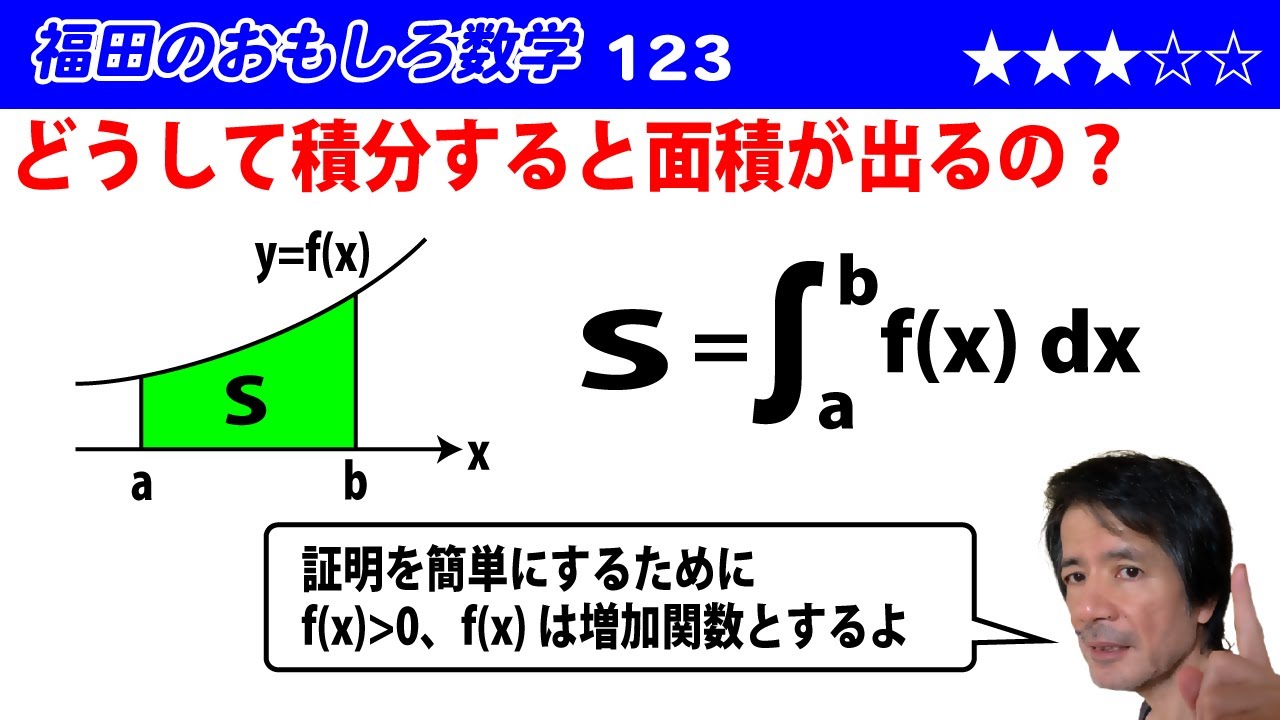
$f(x)$は常に正の値をとる連続な増加関数とする。このとき$y$=$f(x)$のグラフと$x$軸、直線$x$=$a$, $x$=$b$で囲まれる部分の面積を$S$とすると$S$=$\displaystyle\int_a^bf(x)dx$であることを証明せよ。
この動画を見る
$f(x)$は常に正の値をとる連続な増加関数とする。このとき$y$=$f(x)$のグラフと$x$軸、直線$x$=$a$, $x$=$b$で囲まれる部分の面積を$S$とすると$S$=$\displaystyle\int_a^bf(x)dx$であることを証明せよ。
福田の数学〜一橋大学2024年文系第2問〜2つの放物線が共有点で接線直交する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。



