 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題#343「計算のクセが強すぎる」 防衛大学校2013 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
この動画を見る
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
大学入試問題#342「深夜24時ストック0の選択」 岡山県立大学(2013) #定積分
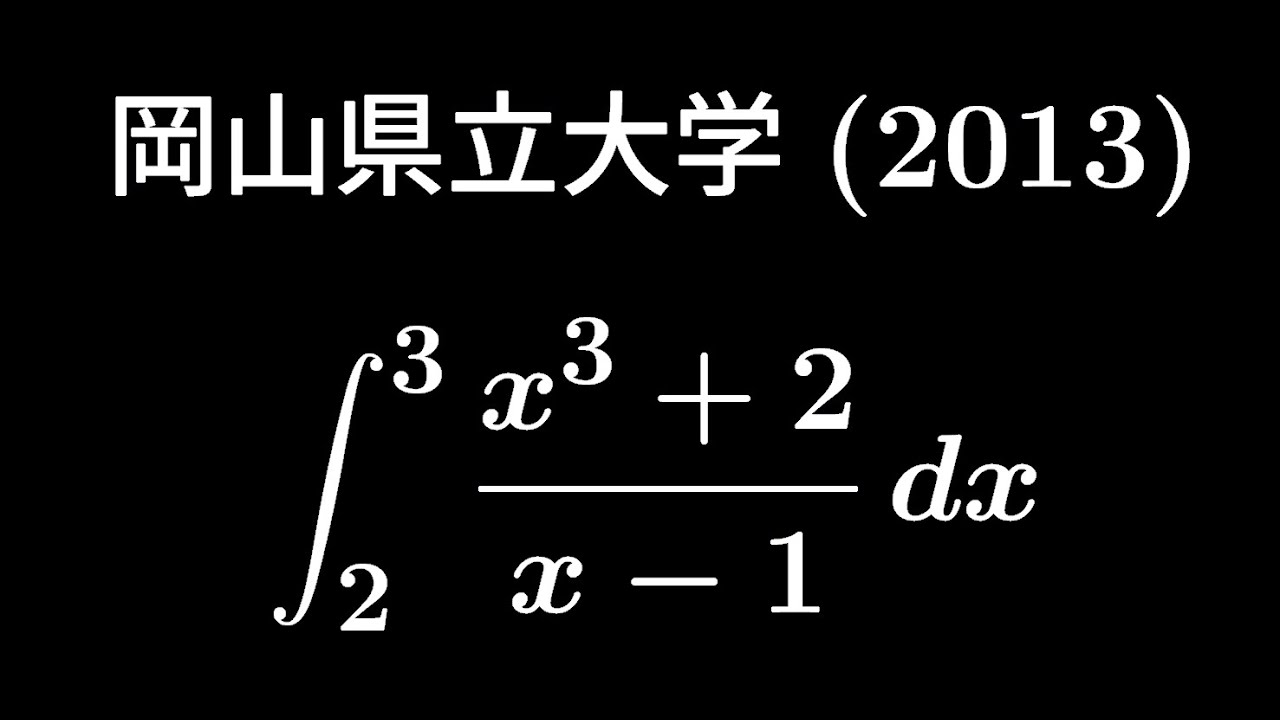
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
大学入試問題#341「部分積分の心を・・・」 立教大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
大学入試問題#340「とりあえず絶対値はずそ」 日本大学医学部(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
大学入試問題#339「とりま部分積分じゃろ~~」 岡山県立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
【超良問】大学入試問題#337 弘前大学(2010) #定積分 #ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
大学入試問題#338 数学トークさん #定積分 #キングプロパティ
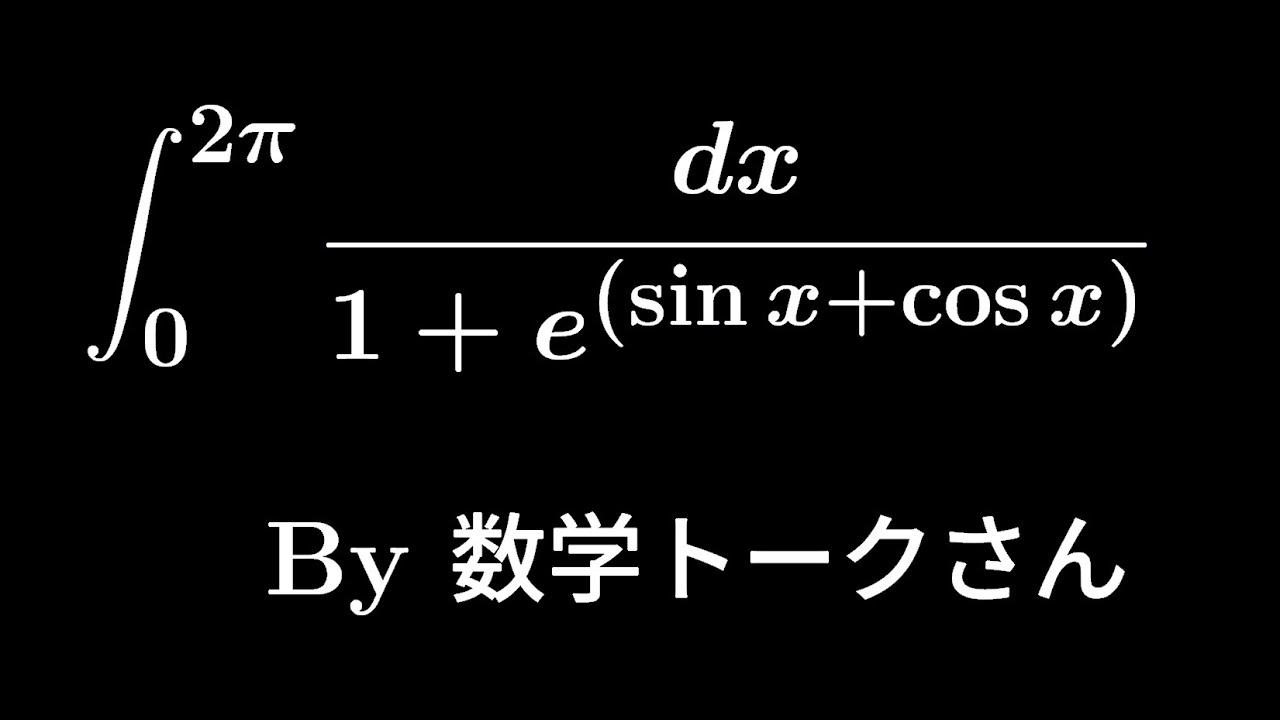
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
この動画を見る
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
大学入試問題#336 横浜国立大学2013 #定積分
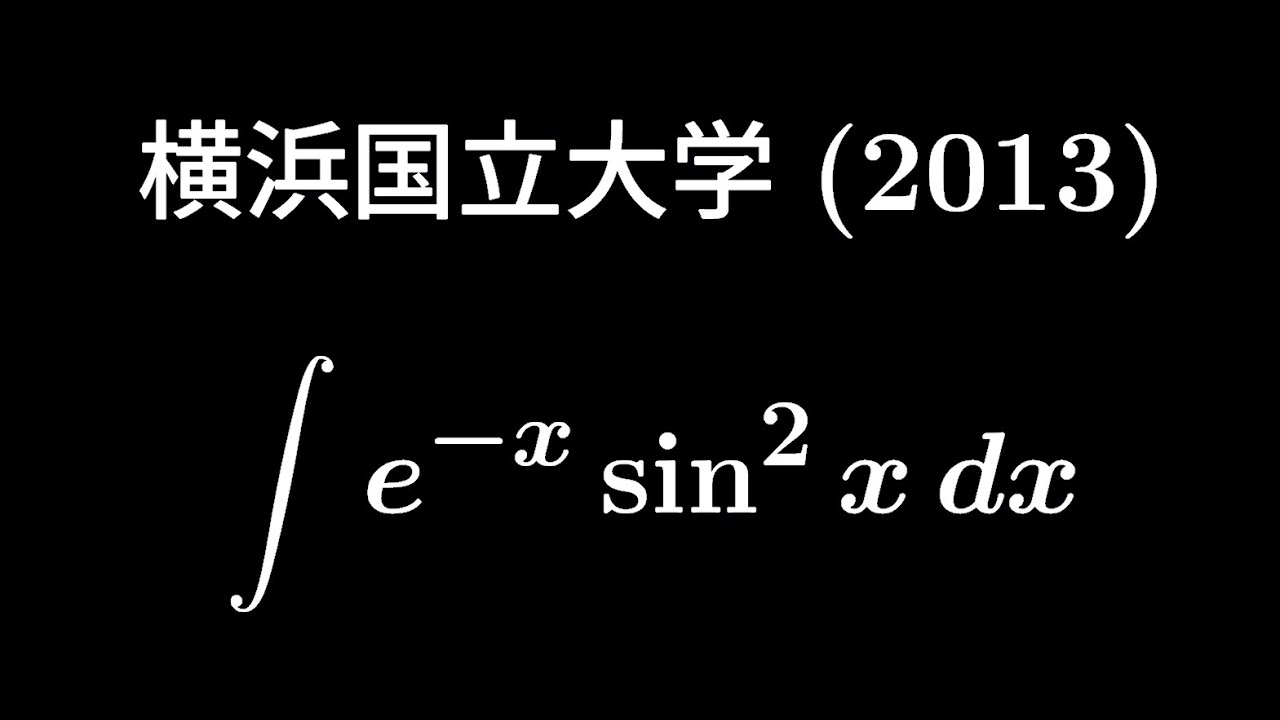
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
大学入試問題#335 防衛医科大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
この動画を見る
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
【最後の足し算で計算ミスしてます。】大学入試問題#334 広島市立大学(2011) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2+1}{x+1}dx$
出典:2011年広島市立大学 入試問題
大学入試問題#333 青山学院大学(2013) #定積分 #極限

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
大学入試問題#332 Instagram #不定積分
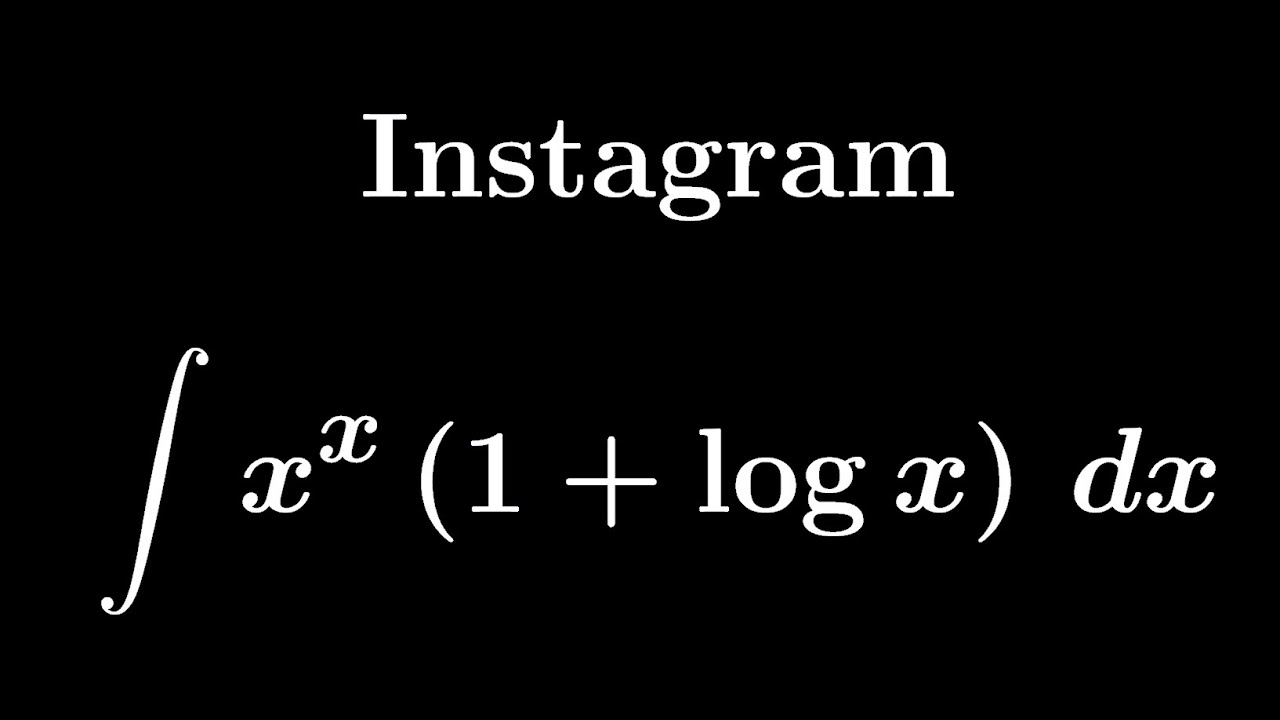
大学入試問題#331 高校教員が作成した問題 #定積分
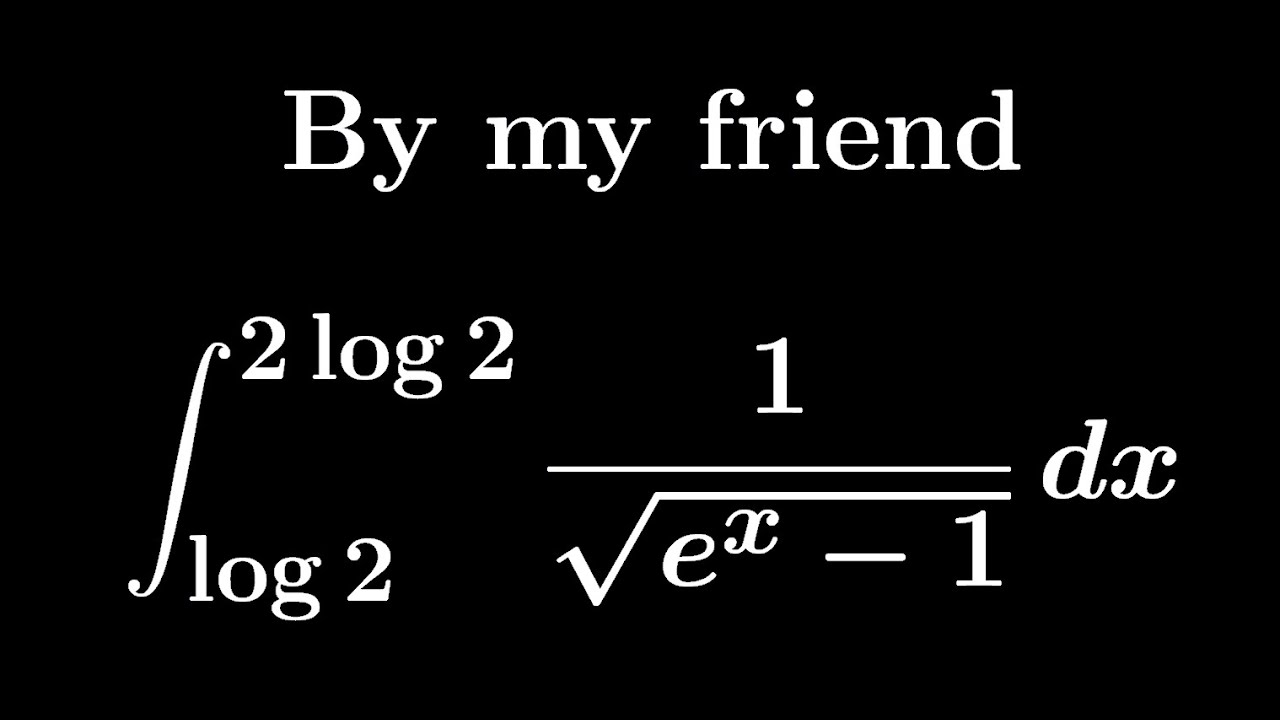
単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log2}^{2log2}\displaystyle \frac{dx}{\sqrt{ e^x-1 }}$
この動画を見る
$\displaystyle \int_{log2}^{2log2}\displaystyle \frac{dx}{\sqrt{ e^x-1 }}$
大学入試問題#330 横浜国立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
大学入試問題#329 熊本大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
大学入試問題#328 金沢大学(2013) #定積分
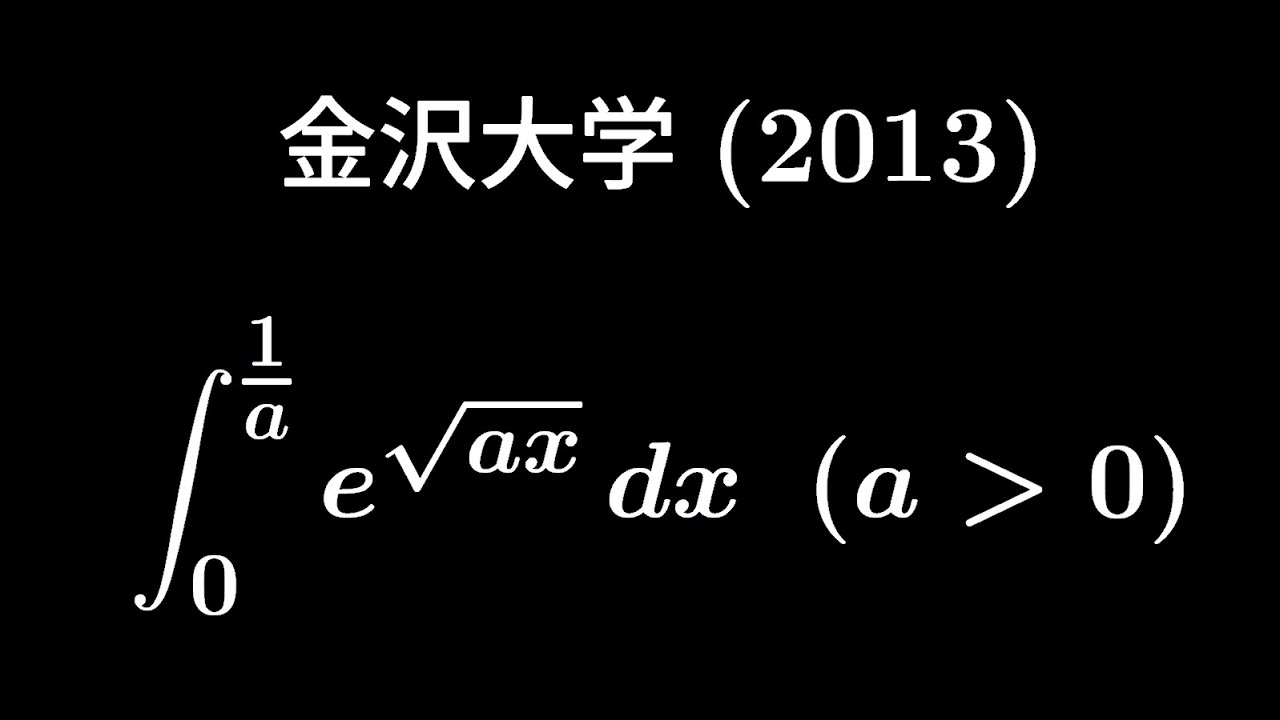
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#金沢大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{\frac{1}{a}}e^{\sqrt{ ax }}dx$
出典:2013年金沢大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{\frac{1}{a}}e^{\sqrt{ ax }}dx$
出典:2013年金沢大学 入試問題
大学入試問題#327 埼玉大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{9+16\sin^2x}dx$
出典:2010年埼玉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{9+16\sin^2x}dx$
出典:2010年埼玉大学 入試問題
【概要欄必読】大学入試問題#326 Instagram #不定積分
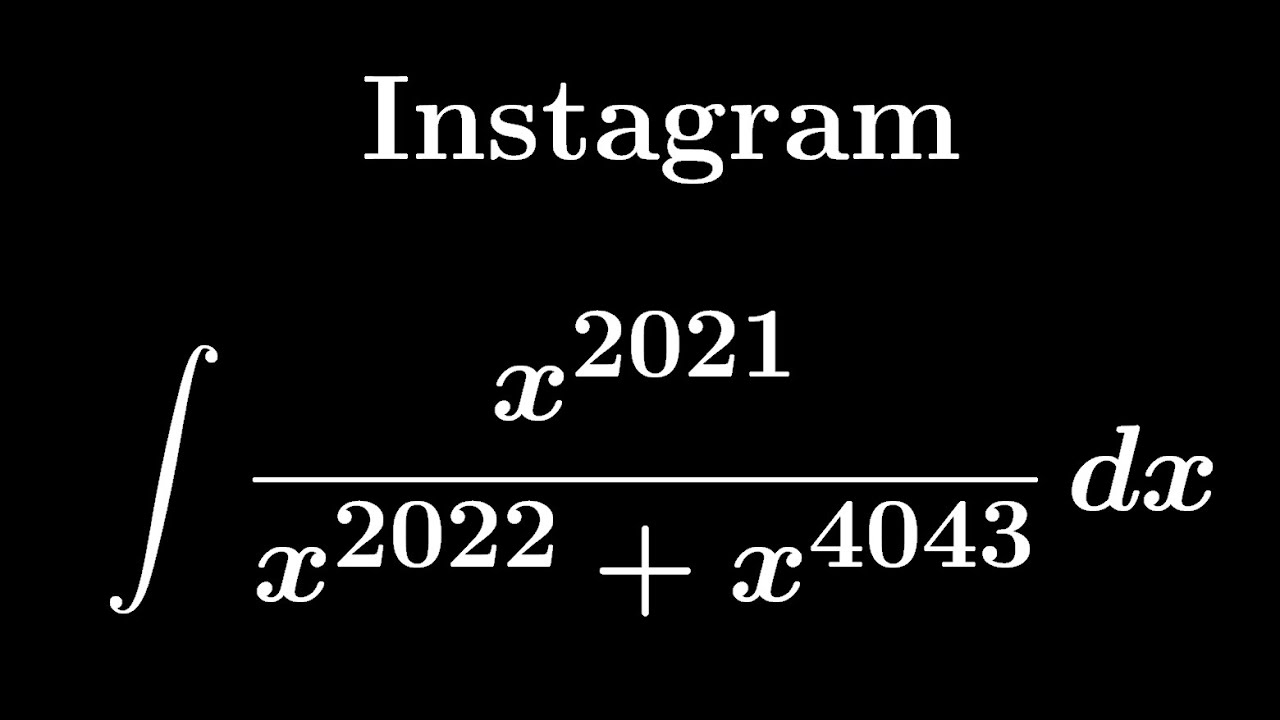
単元:
#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^{2021}}{x^{2022}+x^{4043}}dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x^{2021}}{x^{2022}+x^{4043}}dx$
大学入試問題#325 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
ハルハル様の作成問題⑤ -1 #極限 #ガウス記号

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
この動画を見る
$\theta_n=([x]^n+[\displaystyle \frac{x}{n}])^{\frac{1}{n}}\pi$
(1)
$\displaystyle \lim_{ x \to \infty }\cos\theta_1$
(2)
$\displaystyle \lim_{ x \to \infty }\tan\theta_2$
AkiyaMathさんと学ぶ積分問題 #King_property
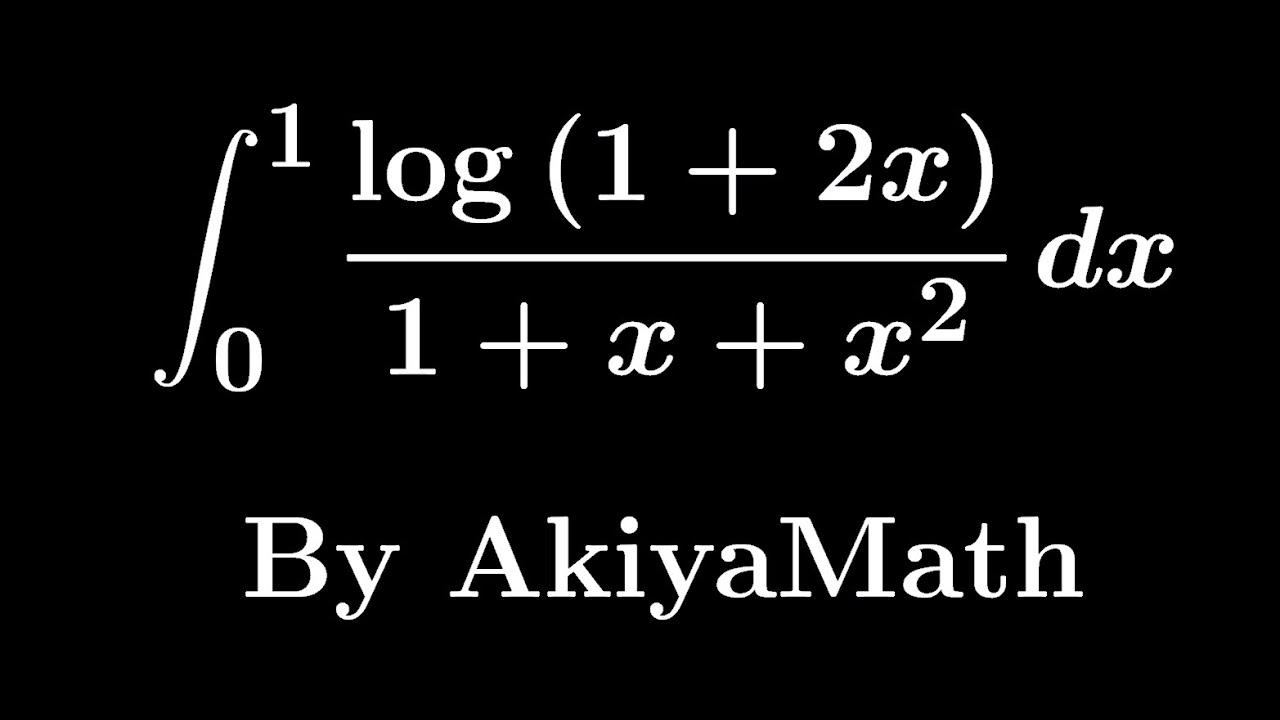
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+2x)}{1+x+x^2}dx$
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+2x)}{1+x+x^2}dx$
大学入試問題#324 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
大学入試問題#323 千葉大学(2010) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$3^n=k^3+1$を満たす正の整数の組$(k,n)$をすべて求めよ。
出典:2010年千葉大学 入試問題
この動画を見る
$3^n=k^3+1$を満たす正の整数の組$(k,n)$をすべて求めよ。
出典:2010年千葉大学 入試問題
【解答にミスあり概要欄】大学入試問題#322 慶應義塾大学(2021) #三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$-\displaystyle \frac{\pi}{2} \leqq \theta \leqq \displaystyle \frac{\pi}{2}$
$4\cos\displaystyle \frac{\theta}{2}(\cos\displaystyle \frac{\theta}{2}+\sin\displaystyle \frac{\theta}{2})$のとき
$\sin\theta$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
大学入試問題#321 甲南大学(2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
大学入試問題#320 宮崎大学 改 (2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
大学入試問題#319 電気通信大学(2010) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
大学入試問題#318 立教大学 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
大学入試問題#317 鳥取大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
大学入試問題#316 群馬大学(2010) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題
この動画を見る
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題



