周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
円錐と内接球３つ D 立教新座（改）2021
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
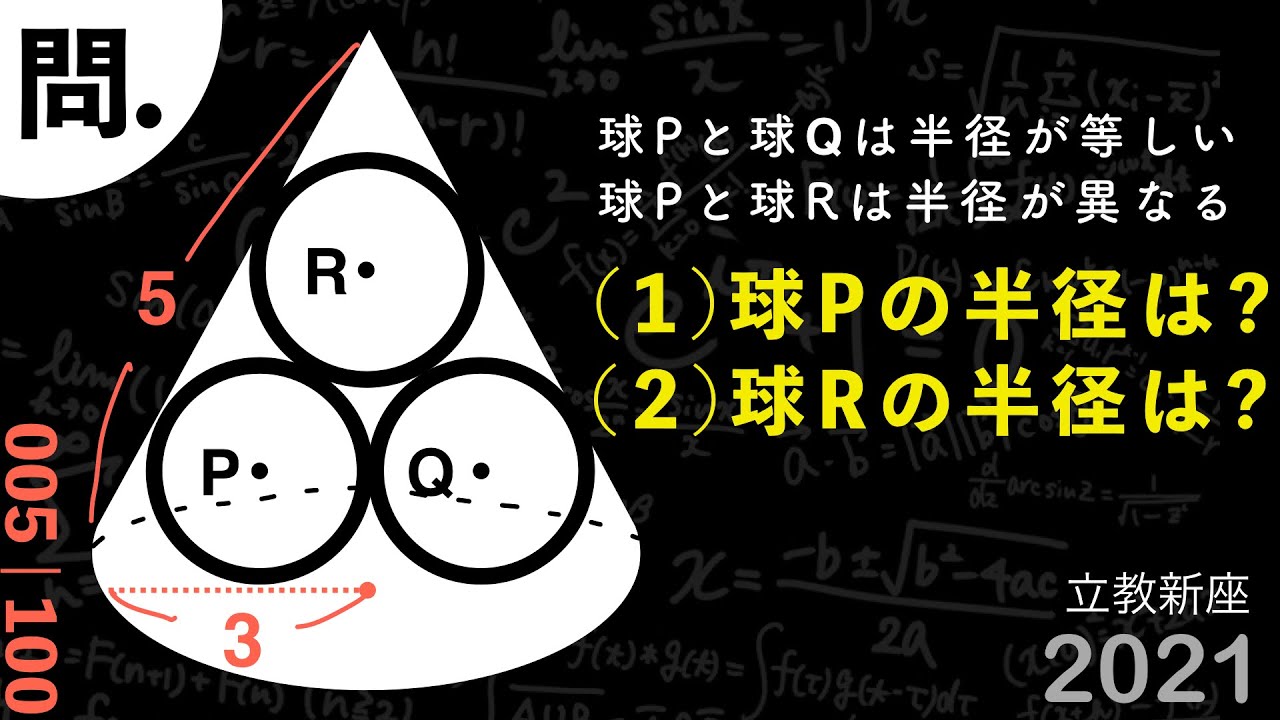
球Pと球Qは半径が等しい
球Pと球Rは半径が異なる
(1)球Pの半径は？
(2)球Rの半径は？
＊図は動画内参照
2021立教新座高等学校（改）
この動画を見る
球Pと球Qは半径が等しい
球Pと球Rは半径が異なる
(1)球Pの半径は？
(2)球Rの半径は？
＊図は動画内参照
2021立教新座高等学校（改）
円錐に内接する立方体 智弁和歌山（改） B
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#立体図形#立体図形その他#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
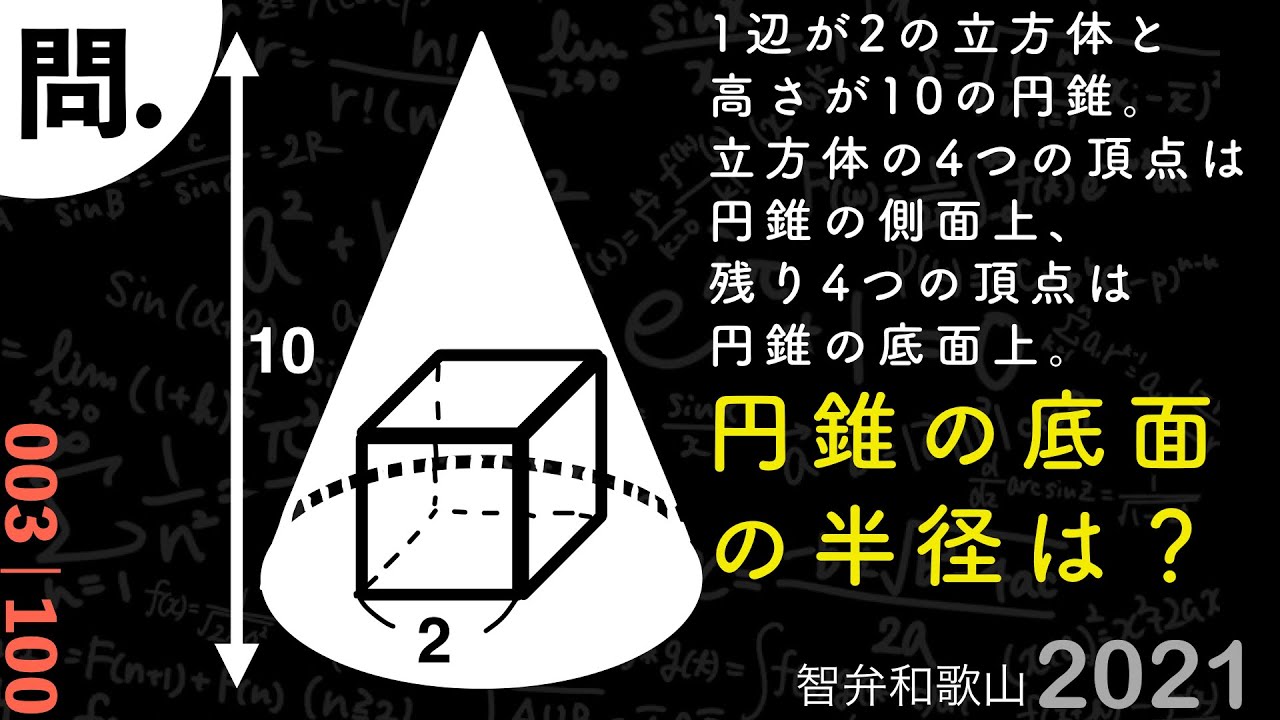
円錐の底面の半径は？
＊図は動画内参照
2021智辯学園和歌山高等学校（改）
この動画を見る
円錐の底面の半径は？
＊図は動画内参照
2021智辯学園和歌山高等学校（改）
難易度MAX 2021ラ・サール最後の問題 D
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
半径1の2つの円が重ならないように正方形内を動く。
円の中心P,Qが存在しうる範囲の面積を求めよ。
＊図は動画内参照
2021ラ・サール高等学校
この動画を見る
半径1の2つの円が重ならないように正方形内を動く。
円の中心P,Qが存在しうる範囲の面積を求めよ。
＊図は動画内参照
2021ラ・サール高等学校
共通テスト2021年数学詳しい解説〜共通テスト2021年IA第５問〜平面幾何
単元：
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large第5問}$
$\triangle ABC$において、$AB=3$, $BC=4$, $AC=5$とする。
$\angle BAC$の二等分線と辺$BC$との交点を$D$とすると
$BD=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$, $AD=\displaystyle \frac{\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}}{\boxed{\ \ オ\ \ }}$
である。
また、$\angle BAC$の二等分線と$\triangle ABC$の外接円$O$との交点で点$A$とは異なる
点を$E$とする。$\triangle AEC$に着目すると
$AE=\boxed{\ \ カ\ \ }\sqrt{\boxed{\ \ キ\ \ }}$
である。
$\triangle ABC$の2辺$AB$と$AC$の両方に接し、外接円$O$に内接する円の中心を
$P$とする。円$P$の半径を$r$とする。さらに、円$P$と外接円$O$との接点を
$F$とし、直線$PF$と外接円$O$との交点で点$F$とは異なる点を$G$とする。
このとき
$AP=\sqrt{\boxed{\ \ ク\ \ }}\ r$, $PG=\boxed{\ \ ケ\ \ }-r$
と表せる。したがって、方べきの定理により$r=\displaystyle \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
$\triangle ABC$の内心を$Q$とする。内接円$Q$の半径は$\boxed{\ \ シ\ \ }$で、$AQ=\sqrt{\boxed{\ \ ス\ \ }}$
である。また、円$P$と辺$AB$との接点を$H$とすると、$AH=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$である。
以上から、点$H$に関する次の$(\textrm{a}),(\textrm{b})$の正誤の組合せとして正しいもの
は$\boxed{\boxed{\ \ タ\ \ }}$である。
$(\textrm{a})$点$H$は3点$B,D,Q$を通る円の周上にある。
$(\textrm{b})$点$H$は3点$B,E,Q$を通る円の周上にある。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
(※選択肢は動画参照)
2021共通テスト過去問
この動画を見る
${\large第5問}$
$\triangle ABC$において、$AB=3$, $BC=4$, $AC=5$とする。
$\angle BAC$の二等分線と辺$BC$との交点を$D$とすると
$BD=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$, $AD=\displaystyle \frac{\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}}{\boxed{\ \ オ\ \ }}$
である。
また、$\angle BAC$の二等分線と$\triangle ABC$の外接円$O$との交点で点$A$とは異なる
点を$E$とする。$\triangle AEC$に着目すると
$AE=\boxed{\ \ カ\ \ }\sqrt{\boxed{\ \ キ\ \ }}$
である。
$\triangle ABC$の2辺$AB$と$AC$の両方に接し、外接円$O$に内接する円の中心を
$P$とする。円$P$の半径を$r$とする。さらに、円$P$と外接円$O$との接点を
$F$とし、直線$PF$と外接円$O$との交点で点$F$とは異なる点を$G$とする。
このとき
$AP=\sqrt{\boxed{\ \ ク\ \ }}\ r$, $PG=\boxed{\ \ ケ\ \ }-r$
と表せる。したがって、方べきの定理により$r=\displaystyle \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
$\triangle ABC$の内心を$Q$とする。内接円$Q$の半径は$\boxed{\ \ シ\ \ }$で、$AQ=\sqrt{\boxed{\ \ ス\ \ }}$
である。また、円$P$と辺$AB$との接点を$H$とすると、$AH=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$である。
以上から、点$H$に関する次の$(\textrm{a}),(\textrm{b})$の正誤の組合せとして正しいもの
は$\boxed{\boxed{\ \ タ\ \ }}$である。
$(\textrm{a})$点$H$は3点$B,D,Q$を通る円の周上にある。
$(\textrm{b})$点$H$は3点$B,E,Q$を通る円の周上にある。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
(※選択肢は動画参照)
2021共通テスト過去問
円錐台 内接球 2021 C
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
球を除いた体積=?
＊図は動画内参照
2021専修大学松戸高等学校
この動画を見る
球を除いた体積=?
＊図は動画内参照
2021専修大学松戸高等学校
2021昭和秀英 正四角錐の外接球
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
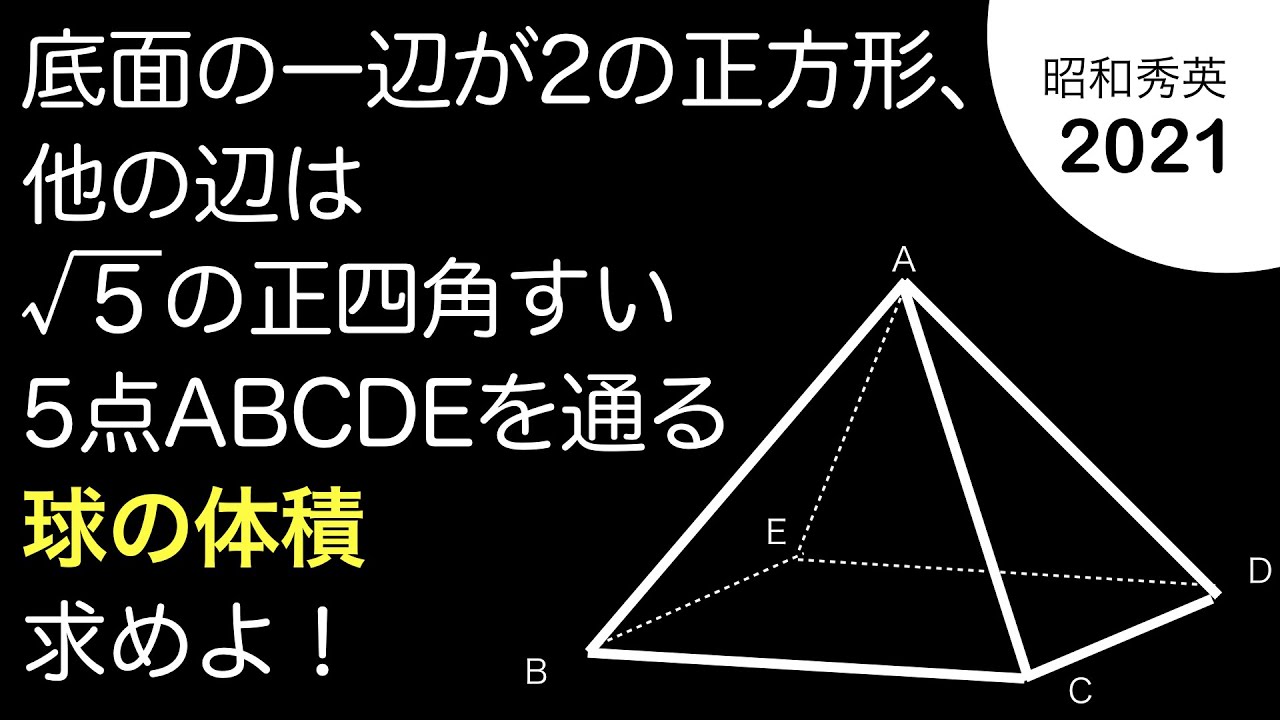
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
＊図は動画内参照
2021昭和学院秀英高等学校
この動画を見る
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
＊図は動画内参照
2021昭和学院秀英高等学校
二つの円 角の二等分線 C
単元：
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
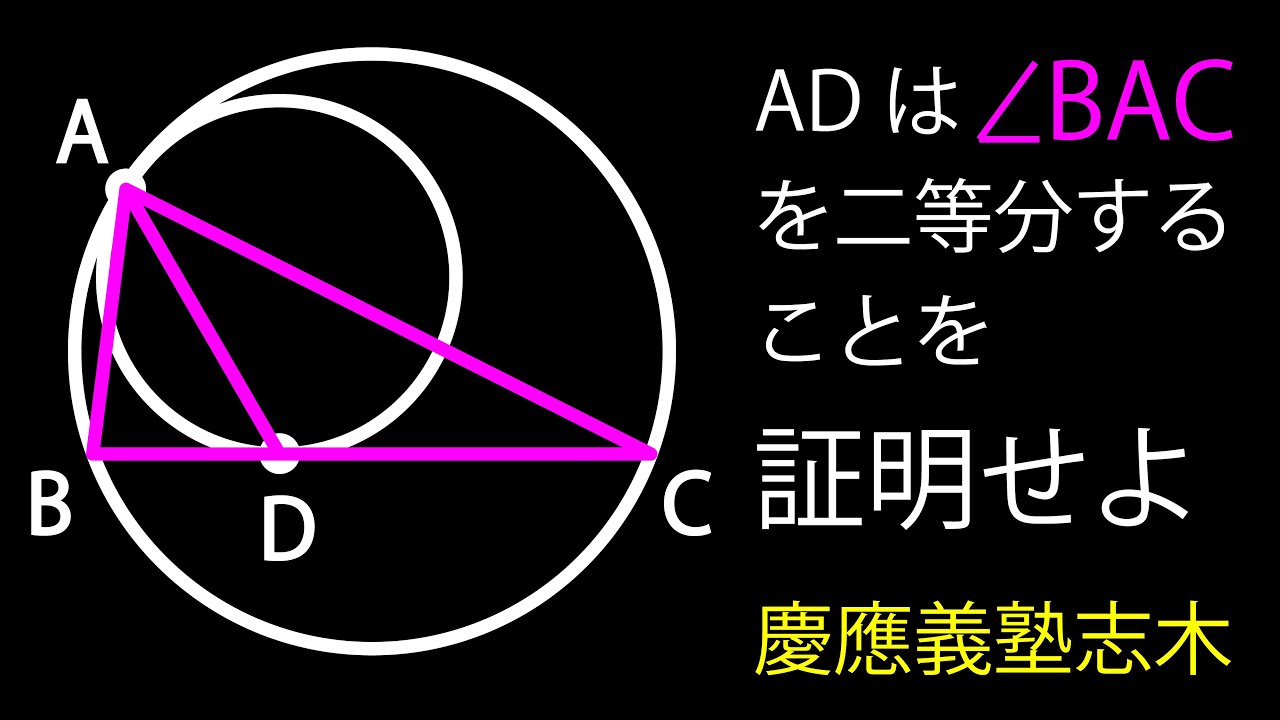
ADは$\angle BAC$を二等分することを示せ
＊図は動画内参照
慶應義塾志木高等学校
この動画を見る
ADは$\angle BAC$を二等分することを示せ
＊図は動画内参照
慶應義塾志木高等学校
円と三平方 中央大附属 C
単元：
#数学(中学生)#中３数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
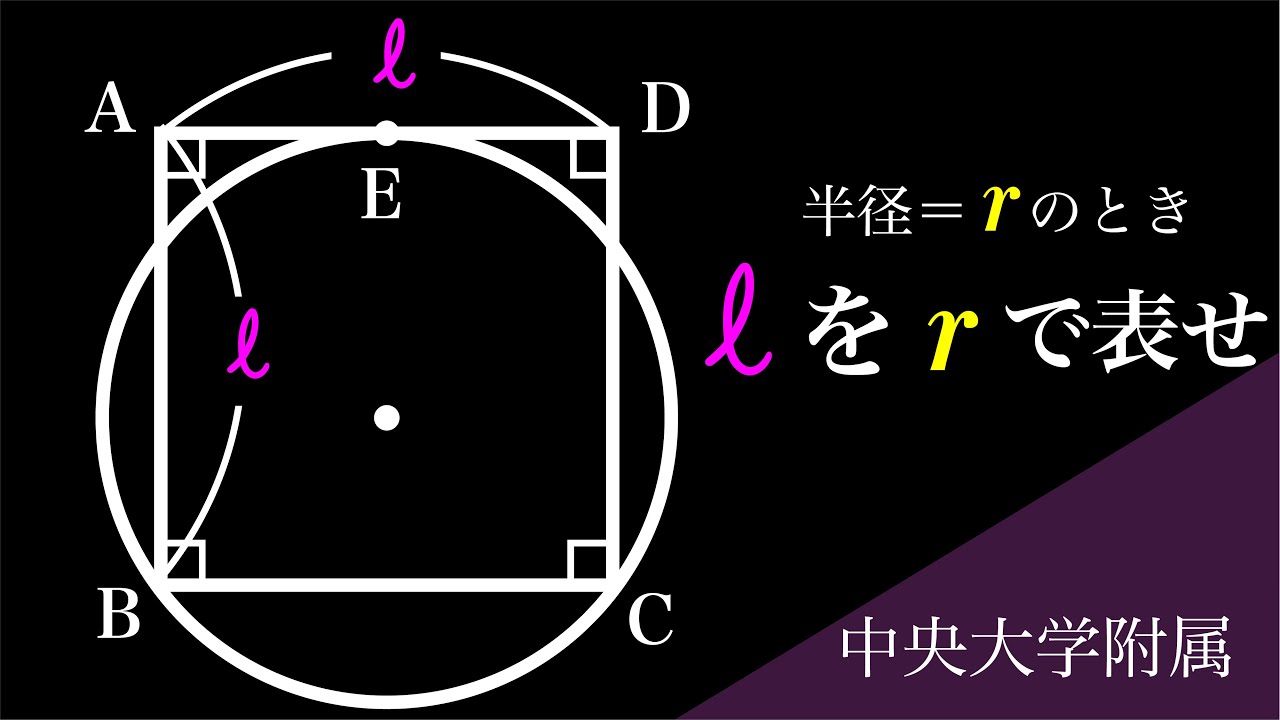
正方形の1辺の長さ=l
半径=r
lをrで表せ
＊図は動画内参照
中央大学附属高等学校
この動画を見る
正方形の1辺の長さ=l
半径=r
lをrで表せ
＊図は動画内参照
中央大学附属高等学校
【数A】図形の性質：正八面体とその内接球の半径の出し方とその過程における注意点を解説！
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
正八面体とその内接球の半径の出し方とその過程における注意点を解説！
この動画を見る
正八面体とその内接球の半径の出し方とその過程における注意点を解説！
【数学A】接弦定理の覚え方と証明【このやり方なら、来週も忘れない】
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
【数学A】接弦定理の覚え方と証明紹介動画です
この動画を見る
【数学A】接弦定理の覚え方と証明紹介動画です
光文社新書「中学の知識でオイラー公式がわかる」Vol.19 ド・モアブルの定理によるアプローチ
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
ド・モアブルの定理によるアプローチ
$(\cos\theta+i \sin\theta)^n=\cos n \theta +i \sin n \theta$
この動画を見る
ド・モアブルの定理によるアプローチ
$(\cos\theta+i \sin\theta)^n=\cos n \theta +i \sin n \theta$
光文社新書「中学の知識でオイラー公式がわかる」Vol.1６ ド・モアブルの定理
光文社新書「中学の知識でオイラー公式がわかる」Vol.10 弧度法を使う理由
一橋大 解説ヨビノリたくみさん 円と放物線の接線
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
原点を中心とする半径$r$の円と、放物線$y=\displaystyle \frac{1}{2}g^2+1$との両方に接する直線のうち、互いに直交するものがある。
$r$の値を求めよ。
出典：1997年一橋大学 過去問
この動画を見る
原点を中心とする半径$r$の円と、放物線$y=\displaystyle \frac{1}{2}g^2+1$との両方に接する直線のうち、互いに直交するものがある。
$r$の値を求めよ。
出典：1997年一橋大学 過去問
名古屋市立（医）放物線と円 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x^2$上の点$(a,a^2)$を中心とし、この放射線に接するような円が存在するための$a$の条件は？
出典：名古屋市立大学 過去問
この動画を見る
$y=x^2$上の点$(a,a^2)$を中心とし、この放射線に接するような円が存在するための$a$の条件は？
出典：名古屋市立大学 過去問
北海道大 双曲線と円の共有点 高校数学 Mathematics Japanese university entrance exam
単元：
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
この動画を見る
$y=\displaystyle \frac{1}{x}$と、$(a,a)$を中心として$(1,1)$を通る円とが$(1,1)$のみを共有するような$a$の範囲$.(a \neq 1)$
出典：北海道大学 過去問
名古屋大 円の方程式 ２円と直線に接する円 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比（三角比・拡張・相互関係・単位円）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)#名古屋大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'08名古屋大学過去問題
2つの円、$x^2+(y-2)^2=9$と$(x-4)^2+(y+4)^2=1$に外接し、x=6と接する円を求めよ。
この動画を見る
'08名古屋大学過去問題
2つの円、$x^2+(y-2)^2=9$と$(x-4)^2+(y+4)^2=1$に外接し、x=6と接する円を求めよ。
【受験対策】数学－図形８
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
この動画を見る
①半径3cmである半球の表面積を求めなさい.
② 右の図1のおうぎ形について,周の長さが$(3\pi+24)cm$のとき,
このおうぎ形の面積を求めなさい.
③右の図2で,四角形$ABCD$は,$AD//BC,AD\lt BC$の台形で,
辺$CD$の中点を$E$とし,辺$BC$の延長と$AE$の延長との交点を$F$とする.
また,頂点$B$から辺$CD$に平行にひいた直線と$EA$の延長との交点を$G$とする.
$\triangle ABF$の面積が$15cm^2$のとき,
$ \triangle DFG$の面積を求めなさい.
図は動画内参照
【高校数学】 数A－６０ 作図④
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①円$O$の外部の点$P$から円$O$に引いた接線を作図しよう.
②線分$AB$を直径とする半円に内接する
正方形$CDEF$を作図しよう.
図は動画内参照
この動画を見る
①円$O$の外部の点$P$から円$O$に引いた接線を作図しよう.
②線分$AB$を直径とする半円に内接する
正方形$CDEF$を作図しよう.
図は動画内参照
【高校数学】 数A－５７ 作図①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の内接円を作図しよう.
②線分$AB$を斜辺とし,他の1辺の長さが$\dfrac{1}{2}AB$である
直角三角形を作図しよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の内接円を作図しよう.
②線分$AB$を斜辺とし,他の1辺の長さが$\dfrac{1}{2}AB$である
直角三角形を作図しよう.
図は動画内参照
【高校数学】 数A－５６ ２つの円の位置関係と共通接線③
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①2つの円がTで内接している.
内側の円の接線が外側の円と交わる点を$A,B$とし,その接点を$P$とする.
このとき,$TP$は$\angle ATB$を2等分することを証明しよう.
図は動画内参照
この動画を見る
①2つの円がTで内接している.
内側の円の接線が外側の円と交わる点を$A,B$とし,その接点を$P$とする.
このとき,$TP$は$\angle ATB$を2等分することを証明しよう.
図は動画内参照
【高校数学】 数A－５５ ２つの円の位置関係と共通接線②
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図で,直線$AB$は円$O,O'$に,それぞれ点$A,B$で接している.
線分$AB$の長さを求めよう.
①円$O,O'$の半径が,それぞれ5,4
中心間の距離が6
②円$O,O'$の半径がそれぞれ6,3
中心間の距離が13
図は動画内参照
この動画を見る
下の図で,直線$AB$は円$O,O'$に,それぞれ点$A,B$で接している.
線分$AB$の長さを求めよう.
①円$O,O'$の半径が,それぞれ5,4
中心間の距離が6
②円$O,O'$の半径がそれぞれ6,3
中心間の距離が13
図は動画内参照
【高校数学】 数A－５４ ２つの円の位置関係と共通接線①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問題1
それぞれの半径が$r,r'(r\gt r')$である2つの円の中心間の距離を$d$とするとき,
①~⑤における$r,r',d$の関係をかこう.
①互いに外部にある
②外接する
③ 2点で交わる
④内接する
⑤一方が他方を含む
問題2
半径が12と5の2つの円の中心間の距離が次のような場合,
2つの円の位置関係と共通接線の数をかこう.
⑥17
⑦6
⑧11
この動画を見る
問題1
それぞれの半径が$r,r'(r\gt r')$である2つの円の中心間の距離を$d$とするとき,
①~⑤における$r,r',d$の関係をかこう.
①互いに外部にある
②外接する
③ 2点で交わる
④内接する
⑤一方が他方を含む
問題2
半径が12と5の2つの円の中心間の距離が次のような場合,
2つの円の位置関係と共通接線の数をかこう.
⑥17
⑦6
⑧11
【高校数学】 数A－５０ 接弦定理
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図において,$\angle x,\angle y$を求めよう.
ただし,直線$\ell,m$は円の接線とする.
①
②
③
④
図は動画内参照
この動画を見る
下の図において,$\angle x,\angle y$を求めよう.
ただし,直線$\ell,m$は円の接線とする.
①
②
③
④
図は動画内参照
【高校数学】 数A－４９ トレミーの定理
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
円に内接する四角形$ABCD$について
$AC･BD=①$である.
②$\triangle ABC$の外接円と$\angle BAC$の
二等分線との交点を$M$とするとき,
$MA=MB+MC$ならば,$AB+AC=2BC$であることを,
トレミーの定理を用いて証明しよう.
図は動画内参照
この動画を見る
円に内接する四角形$ABCD$について
$AC･BD=①$である.
②$\triangle ABC$の外接円と$\angle BAC$の
二等分線との交点を$M$とするとき,
$MA=MB+MC$ならば,$AB+AC=2BC$であることを,
トレミーの定理を用いて証明しよう.
図は動画内参照
【高校数学】 数A－４８ 円に内接する四角形②
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$\triangle ABC$の頂点$A$から,辺$BC$に垂線$AD$を引き,
点$D$から辺$AB,AC$にそれぞれ垂線$DE,DF$を引くと,
4点$E,B,C,F$は同一円周上にあることを証明しよう.
図は動画内参照
この動画を見る
①$\triangle ABC$の頂点$A$から,辺$BC$に垂線$AD$を引き,
点$D$から辺$AB,AC$にそれぞれ垂線$DE,DF$を引くと,
4点$E,B,C,F$は同一円周上にあることを証明しよう.
図は動画内参照
【高校数学】 数A－４７ 円に内接する四角形①
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図で$\angle x$の大きさを求めよう.
①
②
③次の四角形$ABCD$のうち,円に内接するものはどれか.
$\boxed{I}$
$\boxed{II}$
$\boxed{III}$
図は動画内参照
この動画を見る
下の図で$\angle x$の大きさを求めよう.
①
②
③次の四角形$ABCD$のうち,円に内接するものはどれか.
$\boxed{I}$
$\boxed{II}$
$\boxed{III}$
図は動画内参照
【高校数学】 数A－４６ 円周角の定理②
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図で,$L,M,N$はそれぞれ,円に内接する四角形$ABCD$の
辺$AB,BCAD$の中点である.
また,直線$ML$と直線$DA$の交点を$P$,
直線$NL$と直線$CB$の交点を$Q$とする.
このとき,4点$M,N, P,Q$は1つの円周上にあることを証明しよう.
図は動画内参照
この動画を見る
①右の図で,$L,M,N$はそれぞれ,円に内接する四角形$ABCD$の
辺$AB,BCAD$の中点である.
また,直線$ML$と直線$DA$の交点を$P$,
直線$NL$と直線$CB$の交点を$Q$とする.
このとき,4点$M,N, P,Q$は1つの円周上にあることを証明しよう.
図は動画内参照
【高校数学】 数A－４５ 円周角の定理①
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
下の図について,$\angle x$の大きさを求めよう.
①
②
③
④
⑤
⑥
図は動画内参照
この動画を見る
下の図について,$\angle x$の大きさを求めよう.
①
②
③
④
⑤
⑥
図は動画内参照
【高校数学】 数A－３９ 傍心と傍接円
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
三角形の1つの①の①と,他の2つの頂点における
②の②は1点で交わる.この点を傍心という.
③$\triangle ABC$の頂点$A$における内角の二等分線と直線$B,C$
それぞれにおける外角の二等分線は1点で交わることを証明しよう.
図は動画内参照
この動画を見る
三角形の1つの①の①と,他の2つの頂点における
②の②は1点で交わる.この点を傍心という.
③$\triangle ABC$の頂点$A$における内角の二等分線と直線$B,C$
それぞれにおける外角の二等分線は1点で交わることを証明しよう.
図は動画内参照