恒等式・等式・不等式の証明
恒等式・等式・不等式の証明
福田の数学〜京都大学2025文系第5問〜平面が定点を通ることの証明
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#平面上のベクトル#恒等式・等式・不等式の証明#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{5}$
座標空間の$4$点$O,A,B,C$同一平面上にないとする。
$s,t,u$は$0$でない実数とする。
直線$OA$上の点$L$、直線$OB$の点$M$、直線$OC$上の点$N$を
$\overrightarrow{ OL }=s\overrightarrow{ OA},\quad \overrightarrow{ OM }=t\overrightarrow{ OB},\quad \overrightarrow{ ON }=u\overrightarrow{ OC }$
が成り立つようにとる。
$s,t,u$が$\dfrac{1}{s}+\dfrac{2}{t}+\dfrac{3}{u}=4$を満たす範囲で
あらゆる値をとるとき、
$3$点$L,M,N$の定める平面$LMN$は、
$s,t,u$の値に無関係な一定の点を通ることを示せ。
$2025$年京都大学文系過去問題
福田の数学〜京都大学2025文系第2問〜恒等式
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
実数$a,b$についての次の条件(＊)を考える。
(＊)ある実数係数の$2$次式$f(x)$と、
ある実数$c$に対して、
$x$についての恒等式
$\dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \cdots ①$
が成り立つ。
この条件(＊)を満たす点$(a,b)$全体の集合を
座標平面上に図示せよ。
$2025$年京都大学文系過去問題
この動画を見る
$\boxed{2}$
実数$a,b$についての次の条件(＊)を考える。
(＊)ある実数係数の$2$次式$f(x)$と、
ある実数$c$に対して、
$x$についての恒等式
$\dfrac{1}{8}x^4+ax^3+bx^2=f(f(x))+c \cdots ①$
が成り立つ。
この条件(＊)を満たす点$(a,b)$全体の集合を
座標平面上に図示せよ。
$2025$年京都大学文系過去問題
【数Ⅱ】【式と証明】不等式の証明8 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)a>0のとき、a+16/a の最小値を求めよ。
(2)a>0のとき、(a+1/a)(a+16/a) の最小値を求めよ。
(3)a>0 ,b>0 ,ab=12のとき、a+b の最小値を
求めよ。
(4)a>0 ,b>0 ,$2a+3b=4\sqrt{2}$ のとき、abの最大値を求めよ。
この動画を見る
(1)a>0のとき、a+16/a の最小値を求めよ。
(2)a>0のとき、(a+1/a)(a+16/a) の最小値を求めよ。
(3)a>0 ,b>0 ,ab=12のとき、a+b の最小値を
求めよ。
(4)a>0 ,b>0 ,$2a+3b=4\sqrt{2}$ のとき、abの最大値を求めよ。
【数Ⅱ】【式と証明】不等式の証明7 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
a>0,b>0,c>0のとき、(a+b)(b+c)(c+a)≧8abc が成り立つことを証明せよ。また、等号が成り立つのはどのようなときか。
この動画を見る
a>0,b>0,c>0のとき、(a+b)(b+c)(c+a)≧8abc が成り立つことを証明せよ。また、等号が成り立つのはどのようなときか。
【数Ⅱ】【式と証明】不等式の証明6 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$0＜a＜b$ ,$a+b=2$のとき、$1$ ,$ab$ ,$a^2+b^2$ を小さい方から順に並べよ。
この動画を見る
$0＜a＜b$ ,$a+b=2$のとき、$1$ ,$ab$ ,$a^2+b^2$ を小さい方から順に並べよ。
【数Ⅱ】【式と証明】不等式の証明5 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
a>0 ,b>0のとき、$\sqrt{ab}$ , $\displaystyle \frac{2ab}{a+b}$ の大小関係を調べよ。
この動画を見る
a>0 ,b>0のとき、$\sqrt{ab}$ , $\displaystyle \frac{2ab}{a+b}$ の大小関係を調べよ。
【数Ⅱ】【式と証明】不等式の証明4 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
不等式$\sqrt{a^2+b^2}≦|a|+|b|≦\sqrt{2}\sqrt{a^2+b^2}$ を証明せよ。
この動画を見る
不等式$\sqrt{a^2+b^2}≦|a|+|b|≦\sqrt{2}\sqrt{a^2+b^2}$ を証明せよ。
【数Ⅱ】【式と証明】不等式の証明3 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
a>b≧c>0 のとき、次の空欄に記号≧ ,≦ ,> ,<のどれかを記入して正しい関係が成り立つようにせよ。ただし、これが不可能の場合には×とせよ。
(1)$2(ac+b^2 ) □ b(4a+c)$
(2)$a^2+2bc□2ab+ca$
(3)$a^2+2(b^2+c^2) □2a(b+c)$
この動画を見る
a>b≧c>0 のとき、次の空欄に記号≧ ,≦ ,> ,<のどれかを記入して正しい関係が成り立つようにせよ。ただし、これが不可能の場合には×とせよ。
(1)$2(ac+b^2 ) □ b(4a+c)$
(2)$a^2+2bc□2ab+ca$
(3)$a^2+2(b^2+c^2) □2a(b+c)$
【数Ⅱ】【式と証明】不等式の証明2 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の不等式を証明せよ。また、等号が成り立つのはどのようなときか。
(1)$x^2+y^2≧6(x-y-3)$
(2)$a^2-ab+b^2≧a+b-1$
(3)$x^2+xy+y^2+3z(x+y+z)≧0$
(4)$\displaystyle \frac{(a^2+b^2+c^2)}{3}≧\displaystyle \frac{(a+b+c)^2}{3}$
この動画を見る
次の不等式を証明せよ。また、等号が成り立つのはどのようなときか。
(1)$x^2+y^2≧6(x-y-3)$
(2)$a^2-ab+b^2≧a+b-1$
(3)$x^2+xy+y^2+3z(x+y+z)≧0$
(4)$\displaystyle \frac{(a^2+b^2+c^2)}{3}≧\displaystyle \frac{(a+b+c)^2}{3}$
【数Ⅱ】【式と証明】不等式の証明1 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
教材：
#4S数学#4S数学Ⅱ＋BのB問題解説（新課程2022年以降）#式と証明#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の不等式を証明せよ。
(1)$(x^4+y^4)(x^2+y^2 )≧(x^3+y^3 )^2$
(2)$x^4+y^4≧x^3 y+xy^3$
この動画を見る
次の不等式を証明せよ。
(1)$(x^4+y^4)(x^2+y^2 )≧(x^3+y^3 )^2$
(2)$x^4+y^4≧x^3 y+xy^3$
【数Ⅱ】【式と証明】等式の証明6 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1) $x+y+z=-1 ,xy+yz+zx+xyz=0$ ならば、$x ,y ,z$ のうち少なくとも1つは$-1$であることを示せ。
(2) $(bc+ca+ab)(a+b+c)=abc$ならば、$a ,b ,c$ のうちどれか2つの和は$0$であることを示せ。
この動画を見る
(1) $x+y+z=-1 ,xy+yz+zx+xyz=0$ ならば、$x ,y ,z$ のうち少なくとも1つは$-1$であることを示せ。
(2) $(bc+ca+ab)(a+b+c)=abc$ならば、$a ,b ,c$ のうちどれか2つの和は$0$であることを示せ。
【数Ⅱ】【式と証明】等式の証明5 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\dfrac {(x+y)}{2z}=\dfrac{(y+z)}{2x}=\dfrac{(z+x)}{2y}$のとき、この式の値を求めよ。
この動画を見る
$\dfrac {(x+y)}{2z}=\dfrac{(y+z)}{2x}=\dfrac{(z+x)}{2y}$のとき、この式の値を求めよ。
【数Ⅱ】【式と証明】等式の証明4 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x+y+z=0 ,2x^2+2y^2-z^2=0$ のとき、$x=y$ であることを証明せよ。
この動画を見る
$x+y+z=0 ,2x^2+2y^2-z^2=0$ のとき、$x=y$ であることを証明せよ。
【数Ⅱ】【式と証明】等式の証明2 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\dfrac {y+z}{b-c}=\dfrac{z+x}{c-a}=\dfrac{x+y}{a-b}$ のとき、
$x+y+z=0$ であることを証明せよ。
この動画を見る
$\dfrac {y+z}{b-c}=\dfrac{z+x}{c-a}=\dfrac{x+y}{a-b}$ のとき、
$x+y+z=0$ であることを証明せよ。
【数Ⅱ】【式と証明】等式の証明3 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$a:b:c=x:y:z$のとき、
次の等式が成り立つことを証明せよ。
$(a^2+b^2+c^2)(x^2+y^2+z^2)=(ax+by+cz)^2$
この動画を見る
$a:b:c=x:y:z$のとき、
次の等式が成り立つことを証明せよ。
$(a^2+b^2+c^2)(x^2+y^2+z^2)=(ax+by+cz)^2$
【数Ⅱ】【式と証明】等式の証明1 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$a+b+c=0$のとき、
次の等式が成り立つことを証明せよ。
$a(\dfrac1b+\dfrac1c)+b(\dfrac1c+\dfrac1a)+c(\dfrac1a+\dfrac1b)=-3$
この動画を見る
$a+b+c=0$のとき、
次の等式が成り立つことを証明せよ。
$a(\dfrac1b+\dfrac1c)+b(\dfrac1c+\dfrac1a)+c(\dfrac1a+\dfrac1b)=-3$
福田のおもしろ数学417〜条件付きの不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
数列$\{a_n\}$が$a_1=0,a_2=1$
$a_n=5a_{n-1}-a_{n-2} \quad (n \geqq 3)$
を満たしている。
$a_n$が
(1)$5$で割り切れる
(2)$15$で割り切れる
となる$n$を求めて下さい。
この動画を見る
数列$\{a_n\}$が$a_1=0,a_2=1$
$a_n=5a_{n-1}-a_{n-2} \quad (n \geqq 3)$
を満たしている。
$a_n$が
(1)$5$で割り切れる
(2)$15$で割り切れる
となる$n$を求めて下さい。
福田のおもしろ数学416〜条件付きの不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
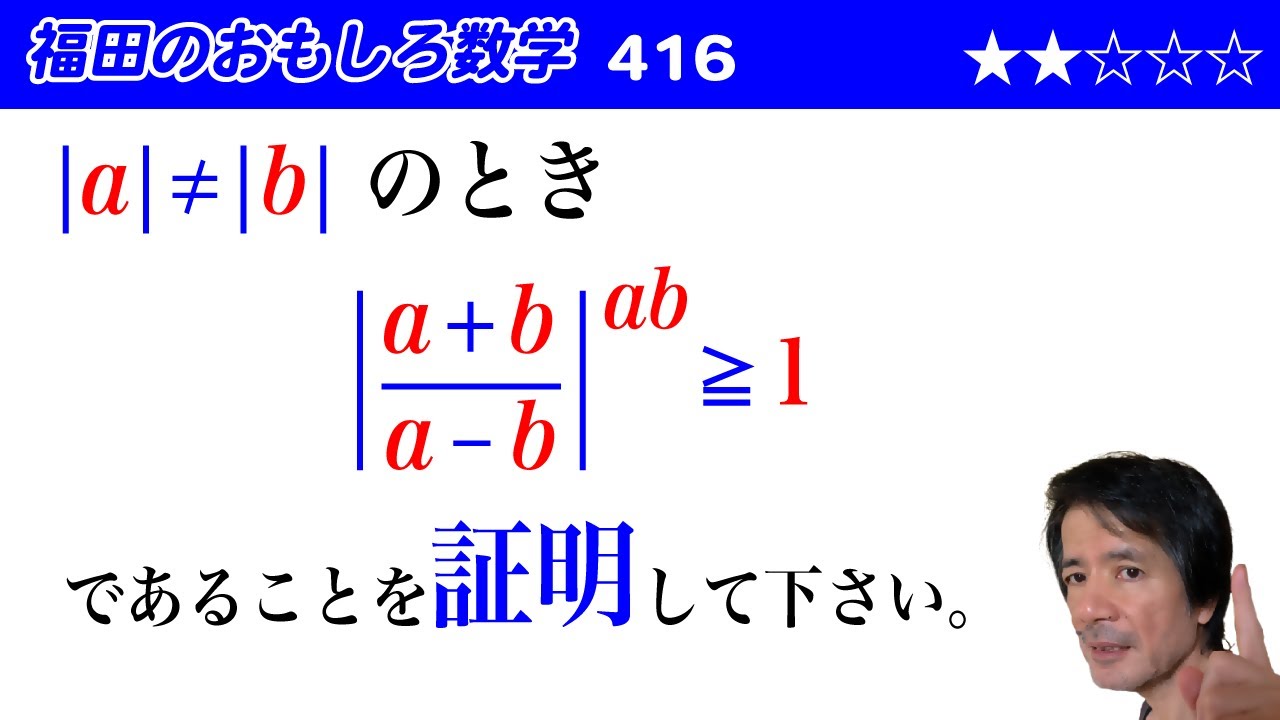
$\vert a \vert \neq \vert b \vert$のとき、
$\left\vert \dfrac{a+b}{a-b}\right \vert^{ab} \geqq 1$
であることを証明して下さい。
この動画を見る
$\vert a \vert \neq \vert b \vert$のとき、
$\left\vert \dfrac{a+b}{a-b}\right \vert^{ab} \geqq 1$
であることを証明して下さい。
福田のおもしろ数学412〜正n角形の内部の点から各辺に下ろした垂線の長さに関する不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
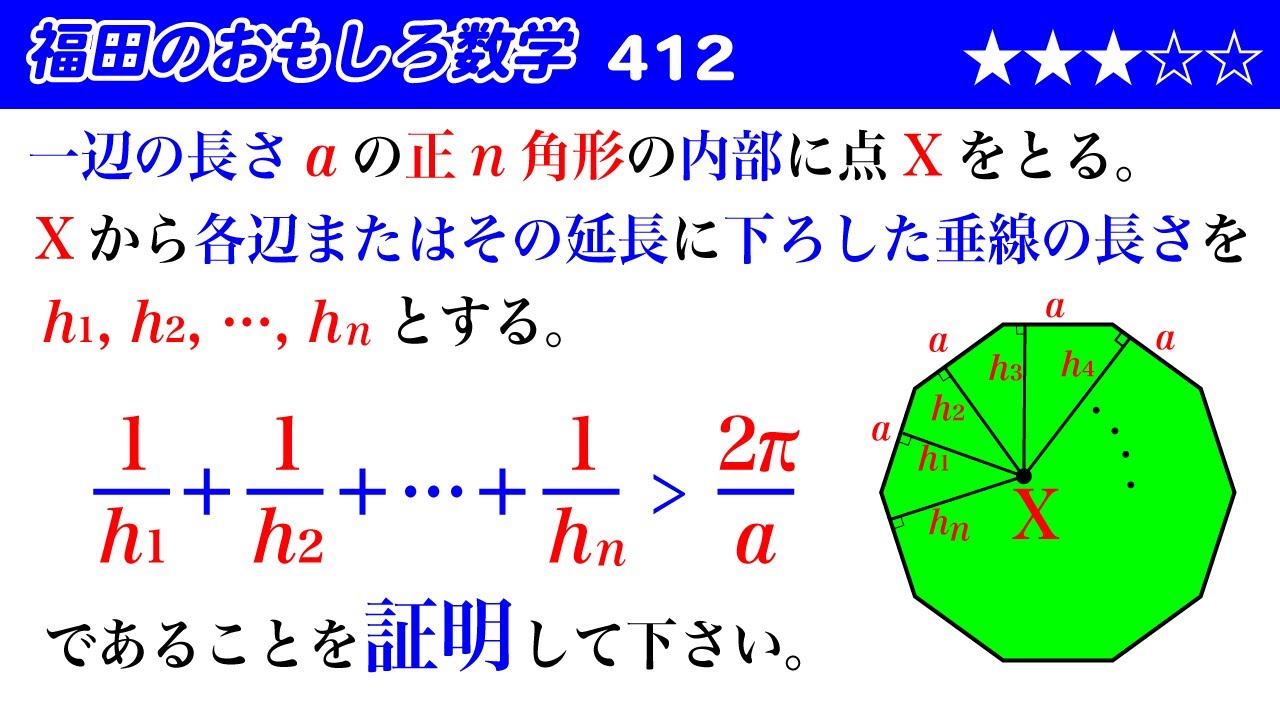
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
この動画を見る
一辺の長さ$a$の正$n$角形の内部に点$X$をとる。
$X$から各辺またはその延長に下ろした垂線の長さを
$h_1,h_2,\cdots h_n$とする。
$\dfrac{1}{h_1}+\dfrac{1}{h_2}+\cdots +\dfrac{1}{h_n} \gt \dfrac{2\pi}{a}$
であることを証明して下さい。
図は動画内参照
福田のおもしろ数学403〜条件付きの不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x+y=2,x\gt 0,y\gt 0$のとき、
$x^3y^3(x^3+y^3)\leqq 2$
を証明して下さい。
この動画を見る
$x+y=2,x\gt 0,y\gt 0$のとき、
$x^3y^3(x^3+y^3)\leqq 2$
を証明して下さい。
福田のおもしろ数学394〜6次の多項式に関する証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
6次の多項式$P(x)$について
$0\lt a \lt b$が
$P(a)=P(-a),P(b)=P(-b),P'(0)=0$
を満たしている。
任意の$x$に対し$P(x)=P(-x)$が
成り立つことを証明せよ。
この動画を見る
6次の多項式$P(x)$について
$0\lt a \lt b$が
$P(a)=P(-a),P(b)=P(-b),P'(0)=0$
を満たしている。
任意の$x$に対し$P(x)=P(-x)$が
成り立つことを証明せよ。
福田のおもしろ数学369〜条件付きの不等式の証明JP
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
この動画を見る
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
福田のおもしろ数学365〜関数方程式を解こう
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
任意の実数 $x$, $y$ に対して
$f(x)f(y)=f(x-y)$
が成り立つような関数 $f(x)$ をすべて求めて下さい。
この動画を見る
任意の実数 $x$, $y$ に対して
$f(x)f(y)=f(x-y)$
が成り立つような関数 $f(x)$ をすべて求めて下さい。
福田のおもしろ数学361〜複雑な関数方程式の解
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数から実数への関数 $f(x)$ が任意の実数 $x$, $y$ に対して
$
f(yf(x+y)+f(x))=4x+2yf(x+y)
$
を満たしている。このような関数 $f(x)$ をすべて求めよ。
この動画を見る
実数から実数への関数 $f(x)$ が任意の実数 $x$, $y$ に対して
$
f(yf(x+y)+f(x))=4x+2yf(x+y)
$
を満たしている。このような関数 $f(x)$ をすべて求めよ。
福田のおもしろ数学348〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師：
福田次郎
問題文全文(内容文)：
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
この動画を見る
$\frac{3}{2} \leqq x \leqq 5$のとき、$2\sqrt{ \mathstrut x+1 }+\sqrt{ \mathstrut 2x-3}+\sqrt{ \mathstrut 15-3x } \lt 2\sqrt{ \mathstrut 19 }$を証明してください。
【数Ⅱ】【式と証明】恒等式2 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
この動画を見る
次の等式が $x,y$についての恒等式となるように、定数$a,b,c$の値を定めよ。
(1) $x^2+y^2=a(x+y)^2+b(x-y)^2 $
(2) $xy=a(x+y)^2+b(x-y)^2$
(3) $x^2+axy+bx-2y+2=(x-1)(x+2y+c)$
【数Ⅱ】【式と証明】恒等式1 ※問題文は概要欄
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
この動画を見る
$(k+1)x-(2k+3)y-3k-5=0$が$k$のどのような値に対しても成り立つように、$x,y$の値を定めよ。
福田のおもしろ数学332〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
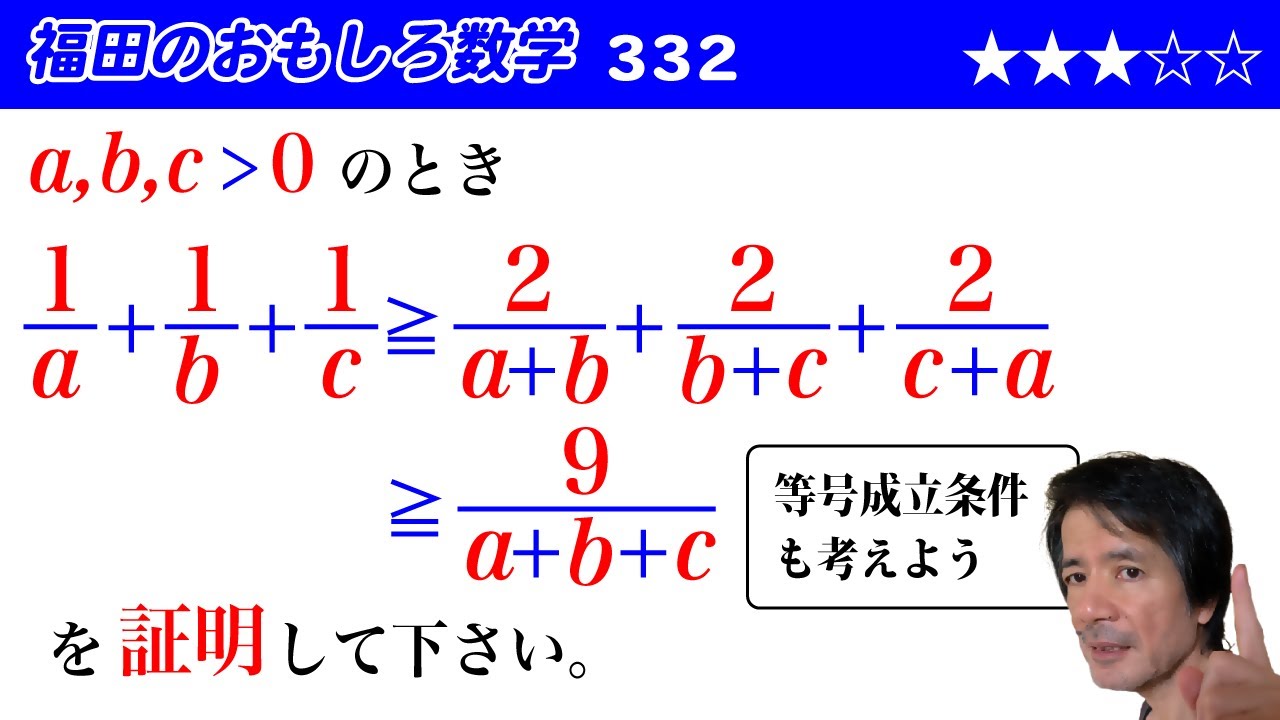
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
この動画を見る
$$a,b,c \gt 0のとき、$$$$\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\geqq\displaystyle \frac{2}{a+b}+\displaystyle \frac{2}{b+c}+\displaystyle \frac{2}{c+a}\geqq\displaystyle \frac{9}{a+b+c}$$
$$を証明してください$$
福田のおもしろ数学331〜連立の不定方程式の整数解
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
この動画を見る
$$\begin{eqnarray}
\begin{cases}
x+y=1-z \\
\ x ^3+y^3=1-z^2
\end{cases}
\end{eqnarray}$$
$$を満たす整数x,y,zを求めよ。$$
福田のおもしろ数学314〜条件付き循環形式の不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師：
福田次郎
問題文全文(内容文)：
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。
この動画を見る
$abc=1$を満たす正の数$a, b, c$に対して$\frac{ab}{a^5+b^5+ab}+\frac{bc}{b^5+c^5+bc}+\frac{ca}{c^5+a^5+ca}\leqq 1$であることを示せ。