 三角関数
三角関数
 三角関数
三角関数
大学入試問題#253 青山学院大学(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
注意ポイントあり!定数分離の良問です【数学 入試問題】【北海道大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
この動画を見る
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
福田の数学〜慶應義塾大学2022年環境情報学部第2問〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
大学入試問題#249 早稲田大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
【9分でマスター!!】とても重要な加法定理を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#三角関数#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
この動画を見る
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
大学入試問題#245 津田塾大学2014 #三角関数 基本的な問題ですが、数IIの範囲で解ける良問だと思いました。

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
この動画を見る
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
福田の数学〜慶應義塾大学2022年商学部第1問(2)〜三角不等式の一般解

単元:
#大学入試過去問(数学)#三角関数#三角関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
式変形だけで解くことができますか?【数学 入試問題】【京都大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\alpha,\beta$が$\alpha>0°,\beta>0°,\alpha+\beta<180°$かつ$ sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$ sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
この動画を見る
$\alpha,\beta$が$\alpha>0°,\beta>0°,\alpha+\beta<180°$かつ$ sin^2\alpha+sin^2\beta=sin^2(\alpha+\beta)$を満たすとき、
$ sin\alpha+sin\beta$の取りうる範囲を求めよ。
京都大過去問
【数Ⅱ】三角関数と方程式 5 三角関数と対称式【t=sinx+cosxで置換しよう】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
この動画を見る
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
【数Ⅱ】三角関数と方程式 4 sinとcosの2次方程式【倍角の公式を使って次数下げ】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
この動画を見る
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
【数Ⅱ】三角関数と方程式 3 三角関数の2次方程式【文字の置き換えをしたら範囲をチェック!】

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
この動画を見る
$(1) \sin2x=\cos x(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0(0 \leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x \cos x-=0(0 \leqq x \lt 2\pi)$
三角関数の合成とか大丈夫ですか?【数学 入試問題】【慶應義塾大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数
$y=2cos^2\theta-\sqrt3 cos\theta sin\theta-sin^2\theta (0≦\theta≦\pi)$
の最大値とその時の$\theta$を求めよ。
慶應義塾大過去問
この動画を見る
関数
$y=2cos^2\theta-\sqrt3 cos\theta sin\theta-sin^2\theta (0≦\theta≦\pi)$
の最大値とその時の$\theta$を求めよ。
慶應義塾大過去問
【数Ⅱ】三角関数と方程式 2 sinとcosの1次方程式【合成して三角関数の個数を減らす】

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)\sin2x=\cos x$$(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1$$(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0$$(0\leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x cos x-1=0$$(0\leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x\cos x-1=0$$(0 \leqq x \lt 2\pi)$
この動画を見る
$(1)\sin2x=\cos x$$(0 \leqq x \lt 2\pi)$
$(2)\sin x+\sqrt3 \cos x=1$$(0 \leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+3=0$$(0\leqq x \lt 2\pi)$
$(4)\sin^2x+\sin x cos x-1=0$$(0\leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x\cos x-1=0$$(0 \leqq x \lt 2\pi)$
【数Ⅱ】三角関数と方程式 1 角のことなる三角関数【倍角の公式を使って角を揃える】

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$(1)\sin 2x=\cos x$$(0\leqq x \leqq 2\pi)$
$(2)\sin x+\sqrt3\cos x=1$$(0\leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+7\sin x+3=0$$(0\leqq x\lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0$$(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x\cos x-1=0$$(0 \leqq x \lt 2\pi)$
この動画を見る
$(1)\sin 2x=\cos x$$(0\leqq x \leqq 2\pi)$
$(2)\sin x+\sqrt3\cos x=1$$(0\leqq x \lt 2\pi)$
$(3)2\sin^2x+7\sin x+7\sin x+3=0$$(0\leqq x\lt 2\pi)$
$(4)\sin^2x+\sin x \cos x-1=0$$(0 \leqq x \lt 2\pi)$
$(5)\sin x+\cos x+2\sin x\cos x-1=0$$(0 \leqq x \lt 2\pi)$
6次式の最大値と最小値!?【数学 入試問題】【自治医科大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
この動画を見る
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
【数Ⅱ】三角関数の合成【加法定理の応用で最頻出! cosへの合成も】

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
(1)$2\sin \left(x+\dfrac{\pi}{3} \right)$を加法定理を用いて展開せよ.
(2)$\sin x+\sqrt3 \cos xをr \sin(x+a)$の形を表せ.
(3)$\sin x+\sqrt3 \cos x$$(0 \leqq x \leqq \pi)$の最大値,最小値を求めよ.
(4)$\sin x-\cos x$を $r \sin(x+a)$の形で表せ.
(5)$2\sin x+3\cos x$を$r \sin(x+a)$の形で表せ.
この動画を見る
(1)$2\sin \left(x+\dfrac{\pi}{3} \right)$を加法定理を用いて展開せよ.
(2)$\sin x+\sqrt3 \cos xをr \sin(x+a)$の形を表せ.
(3)$\sin x+\sqrt3 \cos x$$(0 \leqq x \leqq \pi)$の最大値,最小値を求めよ.
(4)$\sin x-\cos x$を $r \sin(x+a)$の形で表せ.
(5)$2\sin x+3\cos x$を$r \sin(x+a)$の形で表せ.
京大の標準的な問題!三角関数の知識だけで解けます【数学 入試問題】【京都大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ f(\theta)=cos4\theta-4sin^2\theta$とする。$0≦\theta≦\dfrac{3\pi}{4}$における$f(\theta)$の最大値および最小値を求めよ。
京都大過去問
この動画を見る
$ f(\theta)=cos4\theta-4sin^2\theta$とする。$0≦\theta≦\dfrac{3\pi}{4}$における$f(\theta)$の最大値および最小値を求めよ。
京都大過去問
三角比の大小の比較【数学 入試問題】【神戸薬科大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$A,B(A \neq B)$がいずれも鋭角のとき、次の3つの数のうち、最大値は$□$、最小値は$□$である。
$ sin\dfrac{A+B}{2},sin\dfrac{A}{2}+sin\dfrac{B}{2},\dfrac{sinA+sinB}{2}$
神戸薬科大過去問
この動画を見る
$A,B(A \neq B)$がいずれも鋭角のとき、次の3つの数のうち、最大値は$□$、最小値は$□$である。
$ sin\dfrac{A+B}{2},sin\dfrac{A}{2}+sin\dfrac{B}{2},\dfrac{sinA+sinB}{2}$
神戸薬科大過去問
【数Ⅱ】加法定理から出てくる公式【全部自力で導出しよう。暗記、ダメ絶対】

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
(1$)\sin2x=cosx$$(0 \leqq x \lt 2\pi)$を解け.
(2)$t=tan\dfrac{\theta}{2}$とするとき,$\sin\theta,\cos\theta,\tan\theta$をtを用いて表せ.
この動画を見る
(1$)\sin2x=cosx$$(0 \leqq x \lt 2\pi)$を解け.
(2)$t=tan\dfrac{\theta}{2}$とするとき,$\sin\theta,\cos\theta,\tan\theta$をtを用いて表せ.
福田の数学〜筑波大学2022年理系第4問〜2つの三角関数のグラフで囲まれた部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$0 \lt a \lt 4$とする。曲線
$C_1:y= 4\cos^2x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$,
$C_2:y=a-\tan^2x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
は、ちょうど2つの共有点をもつとする。
(1)aの値を求めよ。
(2)$C_1$と$C_2$で囲まれた部分の面積を求めよ。
2022筑波大学理系過去問
この動画を見る
$0 \lt a \lt 4$とする。曲線
$C_1:y= 4\cos^2x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$,
$C_2:y=a-\tan^2x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
は、ちょうど2つの共有点をもつとする。
(1)aの値を求めよ。
(2)$C_1$と$C_2$で囲まれた部分の面積を求めよ。
2022筑波大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第2問〜放物線に反射する直線の方程式と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#微分法と積分法#点と直線#円と方程式#微分とその応用#積分とその応用#接線と法線・平均値の定理#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
福田の数学〜東京医科歯科大学2022年理系第1問〜2つのベクトルで生成される異なる点の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
【超難問】x-1=0が難しすぎる世界

三角関数をサクッと解説!!

三角関数の重要ポイントが詰まった問題【数学 入試問題】【奈良県立医大】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$0<\theta<\pi,\theta \neq \dfrac{\pi}{2}$のとき、
$ tan\theta-\dfrac{1}{tan\theta}=\dfrac{1}{sin\theta}-\dfrac{1}{cos\theta}$を満たす$\theta$の値を求めよ。
奈良県立医大過去問
この動画を見る
$0<\theta<\pi,\theta \neq \dfrac{\pi}{2}$のとき、
$ tan\theta-\dfrac{1}{tan\theta}=\dfrac{1}{sin\theta}-\dfrac{1}{cos\theta}$を満たす$\theta$の値を求めよ。
奈良県立医大過去問
【数Ⅱ】三角比と三角関数の違い【弧度法・グラフ・加法定理の3つだけ。加法定理は証明もしよう】

問題の背景を探る ハンガリーJr数学Olympic
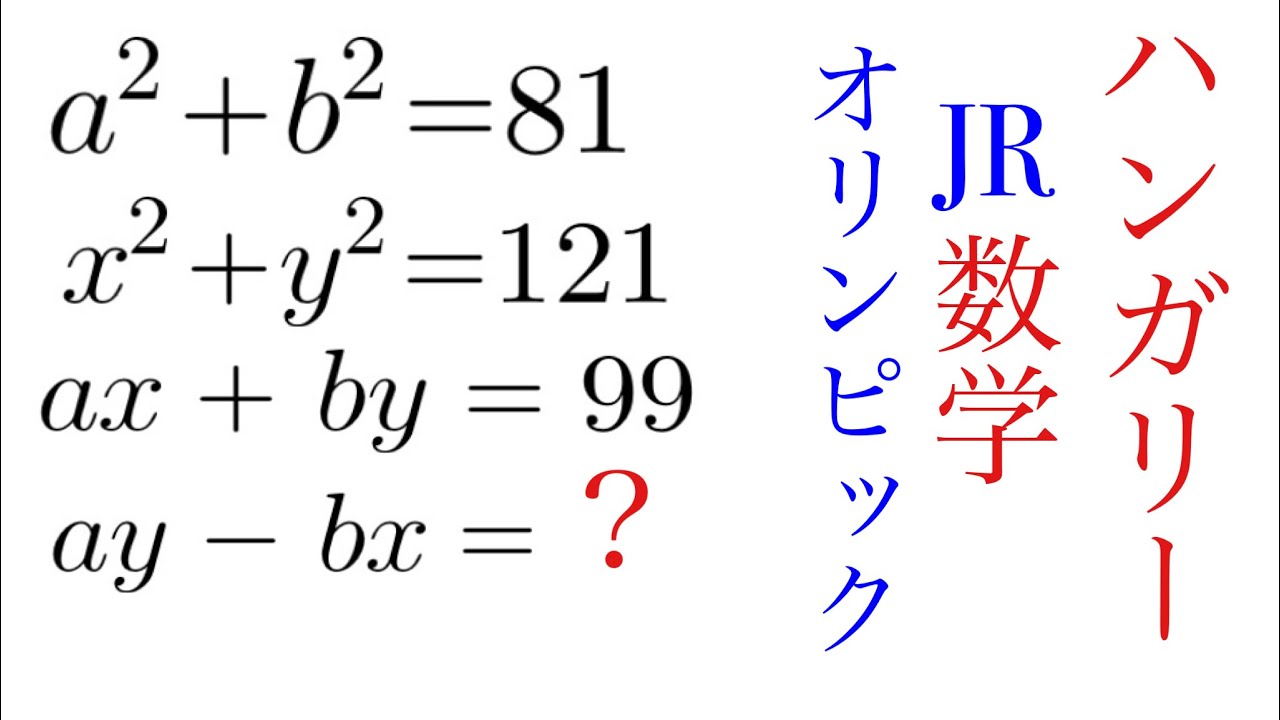
単元:
#複素数平面#円#三角関数#複素数#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
この動画を見る
$ a^2+b^2=81$
$x^2+y^2=121$
$ax+by=99$
$ay-bx=?$
これを解け.
ハンガリーjr数学オリンピック過去問
三角関数の基本問題

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \dfrac{1}{\sin10°}-\dfrac{\sqrt3}{\cos10°}$
これを解け.
この動画を見る
$ \dfrac{1}{\sin10°}-\dfrac{\sqrt3}{\cos10°}$
これを解け.
cos1°は有理数か【数学 入試問題】【チェビシェフ多項式】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数B
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
この動画を見る
(1)$n$を自然数とする。
$cos(n+2)\theta+cos n\theta=2cos(n+1)\theta cos\theta$を示せ。
(2)自然数$n$に対し、$cosn\theta=T_n(cos\theta)$を満たす整数係数の$n$次の整式$T_n(x)$が存在することを示せ。
(3)$cos1°$が無理数であることを証明せよ。
数学入試問題過去問
【有名問題】京都大学の伝説の問題です【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ tan1°$は有理数か?
数学入試問題過去問
この動画を見る
$ tan1°$は有理数か?
数学入試問題過去問
