 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
3つの素数の平方の和が素数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.
この動画を見る
p,q,rは相異なる素数$p^2+q^2+r^2$が素数となるための必要条件を2つ以上挙げてください.
大学入試問題#317 鳥取大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
福田の数学〜立教大学2022年経済学部第1問(5)〜群数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
この動画を見る
自然数n が 2n-1 個続く、初項が1の次のような数列がある。
1,2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5,…
このとき、自然数 m が初めて現れるのは第何項か。
また第 2022項はいくつか。
2022立教学部経済学部過去問
福田の数学〜立教大学2022年経済学部第1問(6)〜平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
この動画を見る
$\boxed{1}$(6)$n$個の値からなるデータがあり,データの値の総和が4,データの値の2乗の総和が26,データの分散が3であるとする.このとき,データの個数$n$は$\boxed{キ}$である.
2022立教大学経済学部過去問
大学入試問題#316 群馬大学(2010) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題
この動画を見る
$2 \leqq p \lt q \lt r$
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r} \geqq 1$をみたす整数の組$(p.g.r)$をすべて求めよ
出典:2010年群馬大学 入試問題
福田の数学〜立教大学2022年経済学部第1問(4)〜表が連続して出ない確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
この動画を見る
コインを5回投げるとき、表が連続して2回以上出ない確率を求めよ。
ただし、コインを1回投げたとき、 表が出る確率および裏が出る確率はそれぞれ1/2であるとする。
2022立教大学経済学部過去問
大学入試問題#315 富山県立大学(2010) #定積分
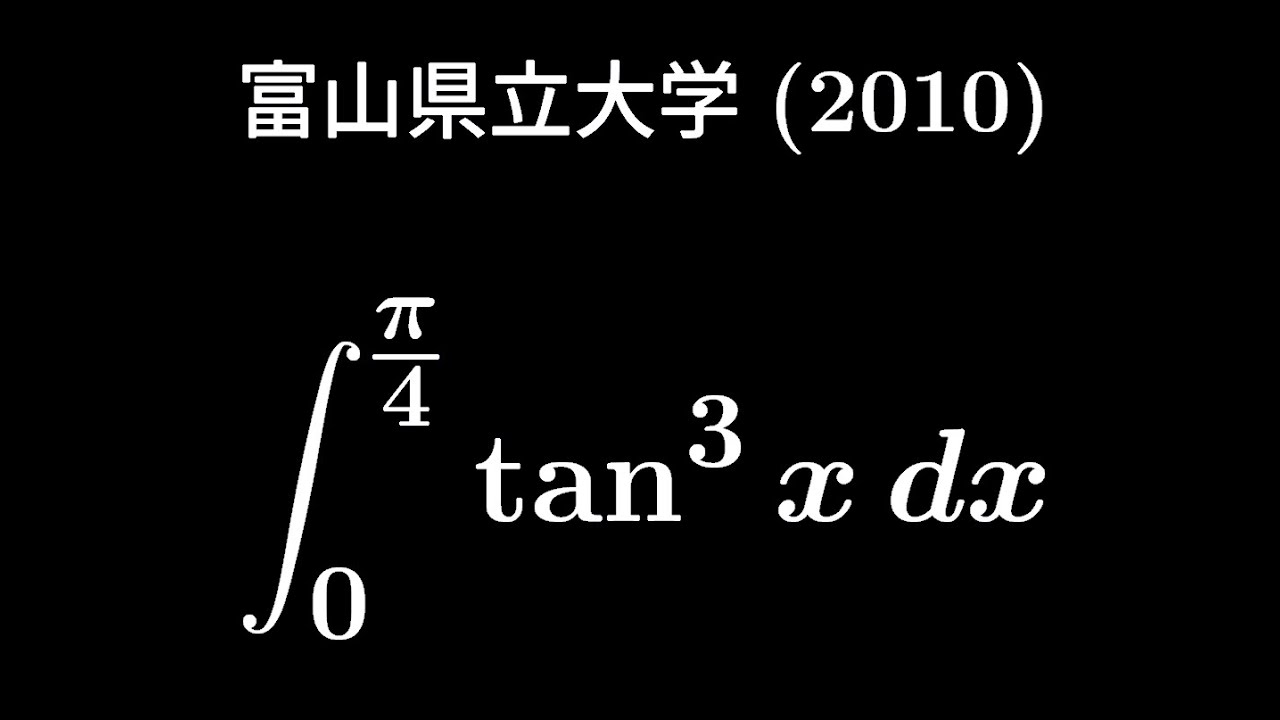
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
福田の数学〜立教大学2022年経済学部第1問(3)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
この動画を見る
aを定数とする。
3次式 $F(x)=x^3-6x+a$を2次式$G(x)=x^2 -3x+2$で割った余りを$R(x)$ とする。
G(x)がR(x)で割り切れるようなaの値をすべて求めよ。
2022立教大学経済学部過去問
大学入試問題#314 弘前大学(2010) #定積分
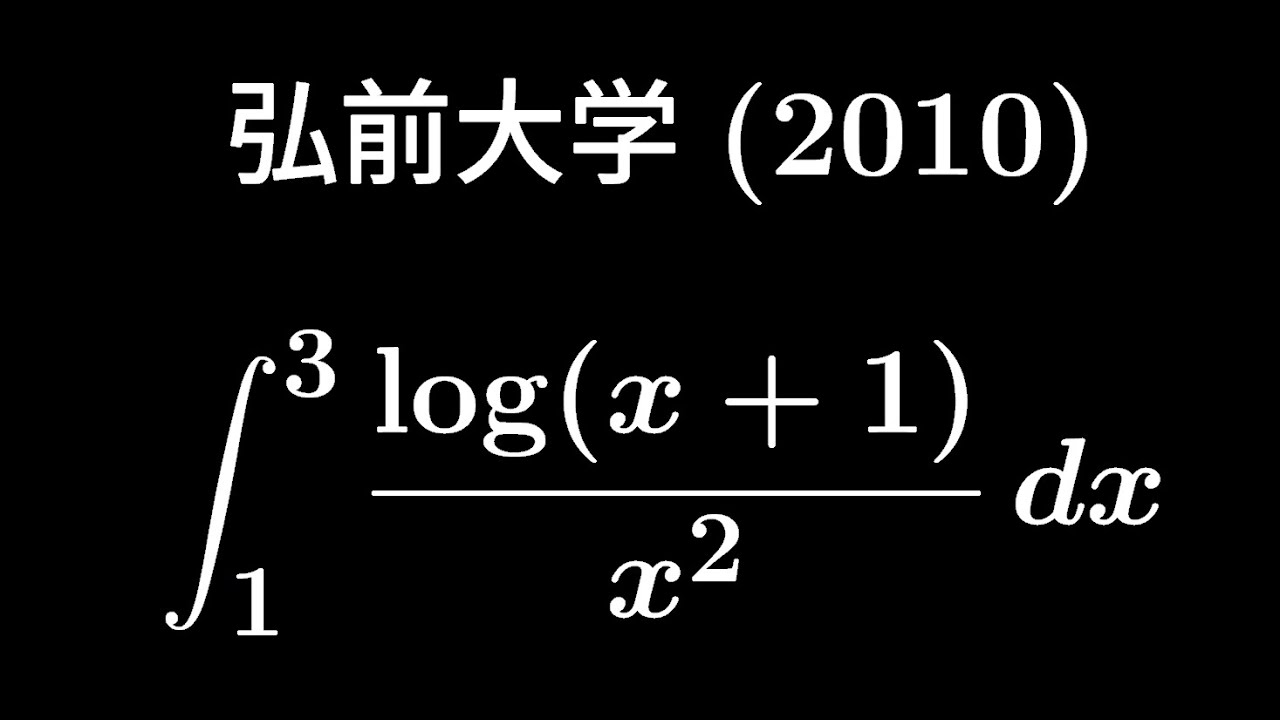
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典:2010年広前大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典:2010年広前大学 入試問題
中学生も解ける??因数分解 福島大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
この動画を見る
因数分解せよ
$x^4+x^2+1+2xy-y^2$
福島大学
福田の数学〜立教大学2022年経済学部第1問(2)〜絶対の付いた方程式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
この動画を見る
$|X-|X-2||=1$の解をすべて求めよ
2022立教大学経済学部過去問
大学入試問題#313 自治医科大学(2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典:2021年自治医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典:2021年自治医科大学 入試問題
工夫が大事!積分と確率の融合問題【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
サイコロを3回投げて出た目を順に$a,b,c$とするとき,
$ \displaystyle \int_{a-3}^{a+3} (x-b)(x-c)dx=0 $
となる確率を求めよ。
一橋大過去問
この動画を見る
サイコロを3回投げて出た目を順に$a,b,c$とするとき,
$ \displaystyle \int_{a-3}^{a+3} (x-b)(x-c)dx=0 $
となる確率を求めよ。
一橋大過去問
福田の数学〜立教大学2022年経済学部第1問(1)〜対称式の値の計算

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x+y=2,1/x+1/y=-1/2$のとき、$|x-y|$の値を求めよ
2022立教大学経済学部過去問
この動画を見る
$x+y=2,1/x+1/y=-1/2$のとき、$|x-y|$の値を求めよ
2022立教大学経済学部過去問
大学入試問題#312 明治大学2021 #定積分 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ k \to \infty }\displaystyle \int_{0}^{1}\displaystyle \frac{e^{kx}-1}{e^{kx}+1}$
出典:2021年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ k \to \infty }\displaystyle \int_{0}^{1}\displaystyle \frac{e^{kx}-1}{e^{kx}+1}$
出典:2021年明治大学 入試問題
福田の数学〜立教大学2022年理学部第4問〜複素数平面上の点列と三角形の面積

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
問題文全文(内容文):
複素数$\alpha=\frac{\sqrt3\ i}{1+\sqrt3\ i}$に対して、複素数$z_n$を
$z_n=8\alpha^{n-1}\ \ \ \ (n=1,\ 2,\ 3,\ ...)$
によって定める。ただしiは虚数単位とする。複素数平面において、原点をOとし、
$z_n$の表す点を$P_n$とする。このとき、以下の問いに答えよ。
(1)$\alpha$の絶対値|$\alpha$と変革$\arg\alpha$をそれぞれ求めよ。
ただし、$0 \leqq \arg\alpha \lt 2\pi$とする。
(2)$z_2,\ z_3$の実部と虚部をそれぞれ求めよ。
(3)$z_n$の極形式をnを用いて表せ。
(4)$O,\ P_n,\ P_{n+1}$を頂点とする三角形の面積$S_n$を$n$を用いて表せ。
(5)(4)で定めた$S_n$に対して、無限級数$\sum_{n=1}^{\infty}S_n$の和Sを求めよ。
2022立教大学理工学部過去問
この動画を見る
複素数$\alpha=\frac{\sqrt3\ i}{1+\sqrt3\ i}$に対して、複素数$z_n$を
$z_n=8\alpha^{n-1}\ \ \ \ (n=1,\ 2,\ 3,\ ...)$
によって定める。ただしiは虚数単位とする。複素数平面において、原点をOとし、
$z_n$の表す点を$P_n$とする。このとき、以下の問いに答えよ。
(1)$\alpha$の絶対値|$\alpha$と変革$\arg\alpha$をそれぞれ求めよ。
ただし、$0 \leqq \arg\alpha \lt 2\pi$とする。
(2)$z_2,\ z_3$の実部と虚部をそれぞれ求めよ。
(3)$z_n$の極形式をnを用いて表せ。
(4)$O,\ P_n,\ P_{n+1}$を頂点とする三角形の面積$S_n$を$n$を用いて表せ。
(5)(4)で定めた$S_n$に対して、無限級数$\sum_{n=1}^{\infty}S_n$の和Sを求めよ。
2022立教大学理工学部過去問
福田の数学〜立教大学2022年理学部第3問〜接線法線と囲まれた部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
この動画を見る
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
大学入試問題#311 杏林大学医学部(2010) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sqrt{ \cos\ 5x }-\sqrt{ \cos\ 3x }}{x^2}$
出典:2010年杏林大学医学部 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sqrt{ \cos\ 5x }-\sqrt{ \cos\ 3x }}{x^2}$
出典:2010年杏林大学医学部 入試問題
ガウス記号×数列!難しそうに見えるけど・・・【一橋大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
実数$x$に対し,$x$を超えない最大の整数を$\lbrack x \rbrack$で表す。数列{$a_k$}を
$a_k=2^{[\sqrt{k}]}$ $(k=1,2,3,・・・)
で定義する。正の整数$n$に対して
$b_n$=$\displaystyle \sum_{k=1}^n^{2} a_k$ を求めよ。
一橋大過去問
この動画を見る
実数$x$に対し,$x$を超えない最大の整数を$\lbrack x \rbrack$で表す。数列{$a_k$}を
$a_k=2^{[\sqrt{k}]}$ $(k=1,2,3,・・・)
で定義する。正の整数$n$に対して
$b_n$=$\displaystyle \sum_{k=1}^n^{2} a_k$ を求めよ。
一橋大過去問
福田の数学〜立教大学2022年理学部第2問〜接線と囲まれた部分の面積と回転体の体積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数xに対し、関数f(x)を
$f(x)=xe^{-x}$
により定める。座標平面上の曲線$C:y=f(x)$に関して、次の問(1)~(5)に答えよ。
(1)f(x)の導関数$f'(x)$を求め、$f(x)$の増減表を書け。ただし、極値も記入すること。
(2)f(x)の第2次導関数$f''(x)$を求め、Cの変曲点の座標を求めよ。
(3)Cの変曲点と、座標平面上の原点を通る直線を$l$とする。
Cとlで囲まれた領域の面積Sを求めよ。
(4)$a,\ b,\ c$を定数とし、関数$g(x)$を$g(x)=(ax^2+bx+c)e^{-2x}$と定める。
$g(x)$の導関数$g'(x)$が$g'(x)=x^2e^{-2x}$を満たすとき、$a,\ b,\ c$の値を求めよ。
(5)Cと(3)で定めたlで囲まれた領域を、x軸の周りに1回転してできる
回転体の体積Vを求めよ。
2022立教大学理学部過去問
この動画を見る
実数xに対し、関数f(x)を
$f(x)=xe^{-x}$
により定める。座標平面上の曲線$C:y=f(x)$に関して、次の問(1)~(5)に答えよ。
(1)f(x)の導関数$f'(x)$を求め、$f(x)$の増減表を書け。ただし、極値も記入すること。
(2)f(x)の第2次導関数$f''(x)$を求め、Cの変曲点の座標を求めよ。
(3)Cの変曲点と、座標平面上の原点を通る直線を$l$とする。
Cとlで囲まれた領域の面積Sを求めよ。
(4)$a,\ b,\ c$を定数とし、関数$g(x)$を$g(x)=(ax^2+bx+c)e^{-2x}$と定める。
$g(x)$の導関数$g'(x)$が$g'(x)=x^2e^{-2x}$を満たすとき、$a,\ b,\ c$の値を求めよ。
(5)Cと(3)で定めたlで囲まれた領域を、x軸の周りに1回転してできる
回転体の体積Vを求めよ。
2022立教大学理学部過去問
因数分解せよ 北京大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$x \sqrt x - 2x + 1$
北京大学
この動画を見る
因数分解せよ
$x \sqrt x - 2x + 1$
北京大学
福田の数学〜立教大学2022年理学部第1問(5)〜最大公約数と最小公倍数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\ a \lt b$ を満たす自然数の組a$,\ b$の和が119、最小公倍数が462であるとき、
$a=\boxed{\ \ キ\ \ },\ b=\boxed{\ \ ク\ \ }$である。
2022立教大学理学部過去問
この動画を見る
$\ a \lt b$ を満たす自然数の組a$,\ b$の和が119、最小公倍数が462であるとき、
$a=\boxed{\ \ キ\ \ },\ b=\boxed{\ \ ク\ \ }$である。
2022立教大学理学部過去問
大学入試問題#310 東京都市大学(2013) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京都市大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}(\cos\ x)log(\sin\ x)dx$
出典:2013年東京都市大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}(\cos\ x)log(\sin\ x)dx$
出典:2013年東京都市大学 入試問題
福田の数学〜立教大学2022年理学部第1問(4)〜解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
この動画を見る
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
大学入試問題#309 明治大学 改 (2013) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}}\cos^5x\ dx$
出典:2013年明治大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\cos^5x\ dx$
出典:2013年明治大学 入試問題
素数が絡んだ整数問題(再アップ)【青山学院大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
素数$p,q$および自然数$n$に対し,$\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{pq}=\dfrac{1}{n}$が成り立つような$(p,q,n)$の組をすべて求めよ。
青山学院大過去問
この動画を見る
素数$p,q$および自然数$n$に対し,$\dfrac{1}{p}+\dfrac{1}{q}+\dfrac{1}{pq}=\dfrac{1}{n}$が成り立つような$(p,q,n)$の組をすべて求めよ。
青山学院大過去問
福田の数学〜立教大学2022年理学部第1問(3)〜垂線の足の位置ベクトル

単元:
#数A#大学入試過去問(数学)#図形の性質#平面上のベクトル#三角形の辺の比(内分・外分・二等分線)#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
三角形ABCにおいて、$AB=5,\ AC=6$、角Aの大きさは$\frac{\pi}{3}$であるとする。
Aから辺BCに垂線AHを下ろす。このとき$BH:CH=\boxed{ウ}:\boxed{エ}$である。
2022立教大学理学部過去問
この動画を見る
三角形ABCにおいて、$AB=5,\ AC=6$、角Aの大きさは$\frac{\pi}{3}$であるとする。
Aから辺BCに垂線AHを下ろす。このとき$BH:CH=\boxed{ウ}:\boxed{エ}$である。
2022立教大学理学部過去問
大学入試問題#308 お茶の水女子大学(2010) #定積分
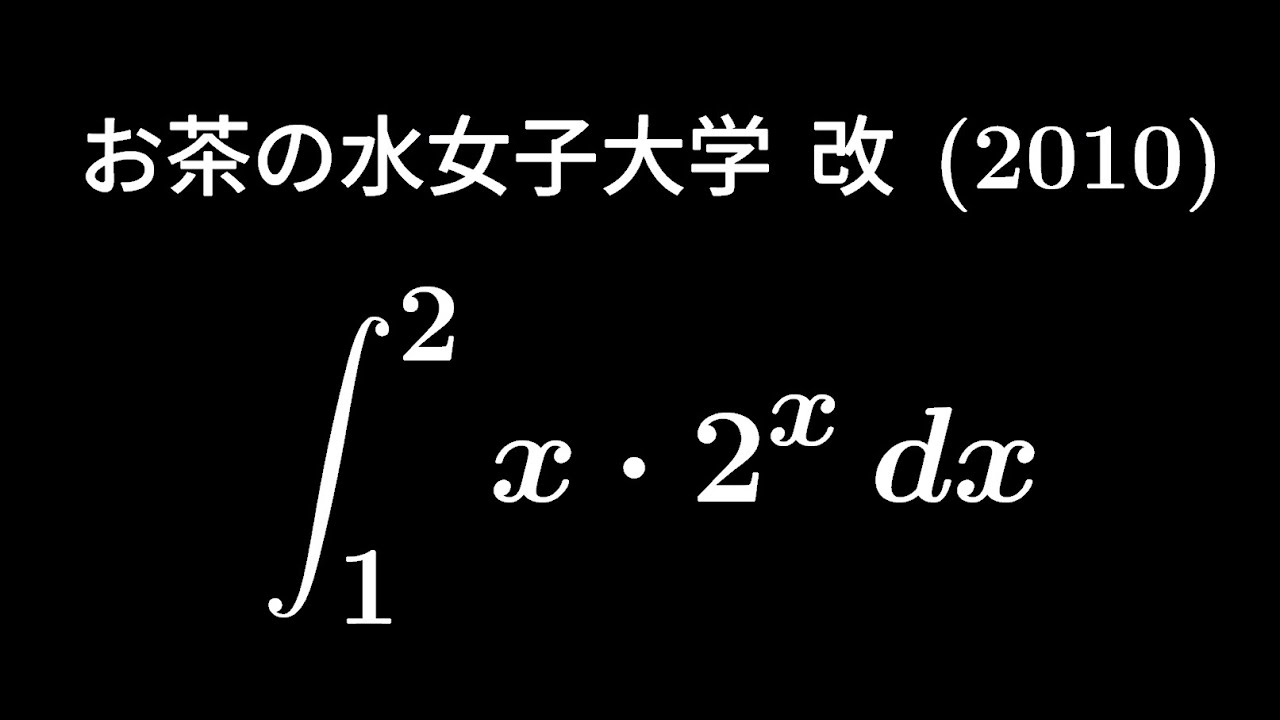
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典:2010年お茶の水女子大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}x\ 2^xdx$
出典:2010年お茶の水女子大学 入試問題
福田の数学〜立教大学2022年理学部第1問(2)〜余事象と確率の加法定理

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
この動画を見る
下図のように1から9までの数字が1つずつ記入された、9枚のカードがある。
$\boxed{1}\ \ \ \boxed{2}\ \ \ \boxed{3}\ \ \ \boxed{4}\ \ \ \boxed{5}\ \ \ \boxed{6}\ \ \ \boxed{7}\ \ \ \boxed{8}\ \ \ \boxed{9}$
これら9枚のカードから同時に取り出した3枚のカードの数字の積が
10で割り切れる確率は$\boxed{イ}$である。
2022立教大学理学部過去問
大学入試問題#307 産業医科大学(2013) #定積分 #King property

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\theta}{2\cos^2(\theta-\displaystyle \frac{\pi}{4})}d\theta$
出典:2013年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\theta}{2\cos^2(\theta-\displaystyle \frac{\pi}{4})}d\theta$
出典:2013年産業医科大学 入試問題
