 数Ⅲ
数Ⅲ
 数Ⅲ
数Ⅲ
高専数学 微積II n次近似式
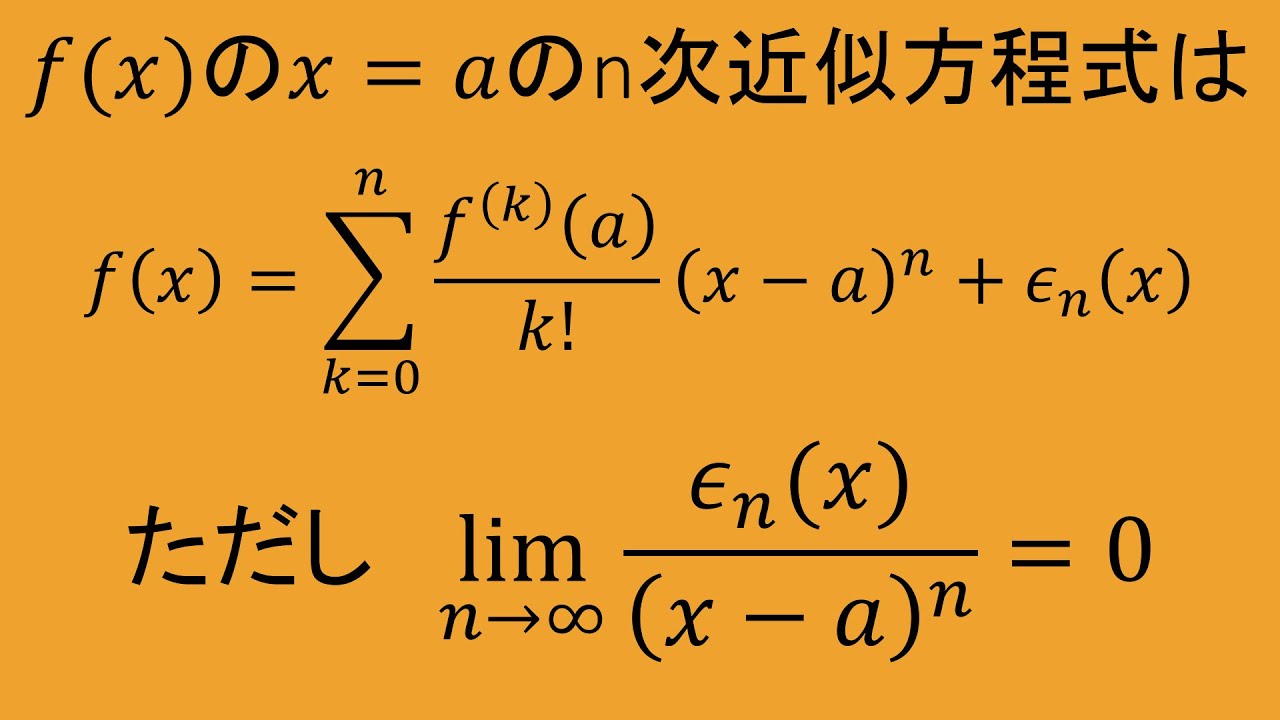
単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
この動画を見る
$f(x)$の$x=a$における$n$次近似式の等式は
$f(x)=\dfrac{f(a)}{O!}+\dfrac{f'(a)}{1!}(x-a)+・・・・・・$
$+\dfrac{f^{(n)}(a)}{n!} (x-a)^n+\xi_n (x)$
つまり
$f(x)=\displaystyle \sum_{k=0}^{n}\dfrac{f^{(k)}(a)}{k!} (x-a)^k+\xi (x)$
ただし
$\displaystyle \lim_{x\to a} \dfrac{\xi_n(x)}{(x-a)^n}=0$
これを解け.
数学「大学入試良問集」【18−7 球に外接する直円錐の最小体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京学芸大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
半径$a$の球に外接する直円錐について、次の各問いに答えよ。
(1)直円錐の底面の半径を$x$とするとき、その高さを$x$を用いて表せ。
(2)このような直円錐の体積の最小値を求めよ。
この動画を見る
半径$a$の球に外接する直円錐について、次の各問いに答えよ。
(1)直円錐の底面の半径を$x$とするとき、その高さを$x$を用いて表せ。
(2)このような直円錐の体積の最小値を求めよ。
高専数学 微積II #1(1)(2) 1次近似式

単元:
#数Ⅱ#微分法と積分法#微分とその応用#速度と近似式#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
この動画を見る
$f(x)$の$x=a$における一次近似式は
$f(a)+f`(a)(x-a)$
次の点における一次近似式を求めよ.
(1)$e^{2x}\cos x \ (x=0)$
(2)$\dfrac{1}{x} \ (x=1)$
18滋賀県教員採用試験(数学:4番 微分方程式)

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$f'(x)$:連続,$f(0)=1$
$g(x)=\displaystyle \int_{0}^{x}(x-t)f'(t)dt$
$f'(x)-1=g'(x)-g''(x)$
をみたす$f(x),g(x)$を求めよ.
この動画を見る
$\boxed{4}$
$f'(x)$:連続,$f(0)=1$
$g(x)=\displaystyle \int_{0}^{x}(x-t)f'(t)dt$
$f'(x)-1=g'(x)-g''(x)$
をみたす$f(x),g(x)$を求めよ.
数学「大学入試良問集」【18−6 平均値の定理と不等式の証明】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#姫路工業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
以下の各問いに答えよ。
(1)
関数$f(x)=x\ log\ x$を微分せよ。
(2)
次の等式を満たす$c$が$x \lt c \lt x+1$の範囲に存在することを示せ。
$(x+1)log(x+1)-x\ log\ x=1+log\ c$
(3)
$x \gt 0$のとき、次の不等式が成り立つことを示せ。
ただし$e$は自然対数の底である。
$\left[ 1+\dfrac{ 1 }{ x } \right]^x \lt e$
この動画を見る
以下の各問いに答えよ。
(1)
関数$f(x)=x\ log\ x$を微分せよ。
(2)
次の等式を満たす$c$が$x \lt c \lt x+1$の範囲に存在することを示せ。
$(x+1)log(x+1)-x\ log\ x=1+log\ c$
(3)
$x \gt 0$のとき、次の不等式が成り立つことを示せ。
ただし$e$は自然対数の底である。
$\left[ 1+\dfrac{ 1 }{ x } \right]^x \lt e$
福田のわかった数学〜高校3年生理系044〜極限(44)関数の連続性(1)

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$数学\textrm{III}$ $関数の連続性(1)$
$\displaystyle f(x) =\lim_{n \to \infty}\frac{x^{2n}-x^{2n-1}+ax^2+bx}{x^{2n}+1}$
が連続関数となるように$aとb$を定めよ。
この動画を見る
$数学\textrm{III}$ $関数の連続性(1)$
$\displaystyle f(x) =\lim_{n \to \infty}\frac{x^{2n}-x^{2n-1}+ax^2+bx}{x^{2n}+1}$
が連続関数となるように$aとb$を定めよ。
数学「大学入試良問集」【18−5 極大値をもつ条件】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \frac{a-\cos\ x}{a+\sin\ x}$が、$0 \lt x \lt \displaystyle \frac{\pi}{2}$の範囲で極大値をもつように、定数$a$の値の範囲を求めよ。
また、その極大値が2となるときの$a$の値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \frac{a-\cos\ x}{a+\sin\ x}$が、$0 \lt x \lt \displaystyle \frac{\pi}{2}$の範囲で極大値をもつように、定数$a$の値の範囲を求めよ。
また、その極大値が2となるときの$a$の値を求めよ。
福田のわかった数学〜高校3年生理系043〜極限(43)有名な極限の証明(3)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(3)\\
\lim_{x \to \infty}\frac{\log x}{x}=0を既知として\\
\lim_{x \to +0}x\log x を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(3)\\
\lim_{x \to \infty}\frac{\log x}{x}=0を既知として\\
\lim_{x \to +0}x\log x を求めよ。
\end{eqnarray}
数学「大学入試良問集」【18−4 微分と不等式の証明】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
この動画を見る
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$のとき、次の不等式が成り立つことを証明せよ。
$\displaystyle \frac{1}{\theta}(\sin\theta+\tan\theta) \gt 2$
福田のわかった数学〜高校3年生理系042〜極限(42)有名な極限の証明(2)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(2)\\
\lim_{x \to \infty}xe^{-x}=0を既知として\\
\lim_{x \to \infty}\frac{\log x}{x} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 有名な極限を証明(2)\\
\lim_{x \to \infty}xe^{-x}=0を既知として\\
\lim_{x \to \infty}\frac{\log x}{x} を求めよ。
\end{eqnarray}
数学「大学入試良問集」【18−2 斜めの漸近線とグラフ】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪工業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)=\displaystyle \frac{x^3}{x^2-1}$とするとき、次の各問いに答えよ。
(1)
$f'(x)$および$f''(x)$を求めよ。
(2)
関数$y=f(x)$の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
(3)
この曲線の漸近線の方程式を求めよ。
この動画を見る
$f(x)=\displaystyle \frac{x^3}{x^2-1}$とするとき、次の各問いに答えよ。
(1)
$f'(x)$および$f''(x)$を求めよ。
(2)
関数$y=f(x)$の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフをかけ。
(3)
この曲線の漸近線の方程式を求めよ。
福田のわかった数学〜高校3年生理系041〜極限(41)有名な極限の証明(1)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 有名な極限を証明(1)
(1)$x \gt 0$で$e^x \gt 1+x+\dfrac{x^2}{2}$ を示せ。
(2)$\displaystyle \lim_{x \to \infty}xe^{-x}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 有名な極限を証明(1)
(1)$x \gt 0$で$e^x \gt 1+x+\dfrac{x^2}{2}$ を示せ。
(2)$\displaystyle \lim_{x \to \infty}xe^{-x}$ を求めよ。
数学「大学入試良問集」【18−1三角関数の微分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#日本女子大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \frac{\sin\ x}{3+\cos\ x}$の最大値を最小値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \frac{\sin\ x}{3+\cos\ x}$の最大値を最小値を求めよ。
福田の数学〜慶應義塾大学2021年医学部第4問〜カテナリーと円の相接

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$
曲線$y=\dfrac{e^x+e^{-x}}{2} (x \gt 0)$を$C$で表す。$\textrm{Q}(X,Y)$を中心とする半径$r$の円が曲線$C$と、点$\textrm{P}(t,\dfrac{e^t+e^{-t}}{2})$ (ただし$t \gt 0$)において共通の接線をもち、さらに$X \lt t$であるとする。このとき$X$および$Y$を$t$の式で表すと
$X=\boxed{\ \ (あ)\ \ }, Y=\boxed{\ \ (い)\ \ }$
となる。$t$の関数$X(t),Y(t)$を$X(t)=\boxed{\ \ (あ)\ \ },Y(t)=\boxed{\ \ (い)\ \ }$により定義する。全ての$t \gt 0$に対して$X(t) \gt 0$となるための条件は、$r$が不等式$\boxed{\ \ (う)\ \ }$を満たすことである。$\boxed{\ \ (う)\ \ }$が成り立たないとき、関数$Y(t)$は$t=\boxed{\ \ (え)\ \ }$において最小値$\boxed{\ \ (お)\ \ }$をとる。また$\boxed{\ \ (う)\ \ }$が成り立つとき、$Y$を$X$の関数と考えて、$(\dfrac{dY}{dX})^2+1$を$Y$の式で表すと$(\dfrac{dY}{dX})^2+1=\boxed{\ \ (か)\ \ }$ となる。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{4}}$
曲線$y=\dfrac{e^x+e^{-x}}{2} (x \gt 0)$を$C$で表す。$\textrm{Q}(X,Y)$を中心とする半径$r$の円が曲線$C$と、点$\textrm{P}(t,\dfrac{e^t+e^{-t}}{2})$ (ただし$t \gt 0$)において共通の接線をもち、さらに$X \lt t$であるとする。このとき$X$および$Y$を$t$の式で表すと
$X=\boxed{\ \ (あ)\ \ }, Y=\boxed{\ \ (い)\ \ }$
となる。$t$の関数$X(t),Y(t)$を$X(t)=\boxed{\ \ (あ)\ \ },Y(t)=\boxed{\ \ (い)\ \ }$により定義する。全ての$t \gt 0$に対して$X(t) \gt 0$となるための条件は、$r$が不等式$\boxed{\ \ (う)\ \ }$を満たすことである。$\boxed{\ \ (う)\ \ }$が成り立たないとき、関数$Y(t)$は$t=\boxed{\ \ (え)\ \ }$において最小値$\boxed{\ \ (お)\ \ }$をとる。また$\boxed{\ \ (う)\ \ }$が成り立つとき、$Y$を$X$の関数と考えて、$(\dfrac{dY}{dX})^2+1$を$Y$の式で表すと$(\dfrac{dY}{dX})^2+1=\boxed{\ \ (か)\ \ }$ となる。
2021慶應義塾大学医学部過去問
福田のわかった数学〜高校3年生理系040〜極限(40)関数の極限、色々な極限(10)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 色々な極限(10)
$\displaystyle \lim_{x \to \infty}(2x+3)\sin(\log(x+3)-$$\log x)$
を求めよ。
この動画を見る
数学$\textrm{III}$ 色々な極限(10)
$\displaystyle \lim_{x \to \infty}(2x+3)\sin(\log(x+3)-$$\log x)$
を求めよ。
【17−9 自然対数の底と極限】を宇宙一わかりやすく「数学大学入試良問集」

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$n$を2以上の整数とする。
平面上に$n+2$個の点$O,P_1,P_2・・・P_n$があり、次の2つの条件を満たしている。
①$\angle P_{k-1}OP_k=\displaystyle \frac{\pi}{n}(1 \leqq k \leqq n),\angle OP_{k-1}P_k=\angle OP_0P_1(2 \leqq k \leqq n)$
②線分$OP_0$の長さは1、線分$OP_1$の長さは$1+\displaystyle \frac{1}{n}$である。
線分$P_{k-1}P_k$の長さを$a_k$とし、$s_n=\displaystyle \sum_{k=1}^n a_k$とおくとき、$\displaystyle \lim_{ n \to \infty }s_n$を求めよ。
この動画を見る
$n$を2以上の整数とする。
平面上に$n+2$個の点$O,P_1,P_2・・・P_n$があり、次の2つの条件を満たしている。
①$\angle P_{k-1}OP_k=\displaystyle \frac{\pi}{n}(1 \leqq k \leqq n),\angle OP_{k-1}P_k=\angle OP_0P_1(2 \leqq k \leqq n)$
②線分$OP_0$の長さは1、線分$OP_1$の長さは$1+\displaystyle \frac{1}{n}$である。
線分$P_{k-1}P_k$の長さを$a_k$とし、$s_n=\displaystyle \sum_{k=1}^n a_k$とおくとき、$\displaystyle \lim_{ n \to \infty }s_n$を求めよ。
数学「大学入試良問集」【17−8 不等式とハサミウチの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の各問いに答えよ。
(1)
$h \gt 0$として、不等式$(1+h)^n \geqq 1+nh+\displaystyle \frac{n(n-1)}{2}h^2$がすべての自然数$n$について成り立つことを数学的帰納法を用いて説明せよ。
(2)
(1)の不等式を使って、$0 \lt x \lt 1$のとき、数列$\{nx^n\}$が$0$に収束することを示せ。
(3)
$0 \lt x \lt 1$のとき
無限級数$2x+4x^2+6x^3+・・・+2nx^n+・・・$の和を求めよ。
この動画を見る
次の各問いに答えよ。
(1)
$h \gt 0$として、不等式$(1+h)^n \geqq 1+nh+\displaystyle \frac{n(n-1)}{2}h^2$がすべての自然数$n$について成り立つことを数学的帰納法を用いて説明せよ。
(2)
(1)の不等式を使って、$0 \lt x \lt 1$のとき、数列$\{nx^n\}$が$0$に収束することを示せ。
(3)
$0 \lt x \lt 1$のとき
無限級数$2x+4x^2+6x^3+・・・+2nx^n+・・・$の和を求めよ。
福田のわかった数学〜高校3年生理系039〜極限(39)関数の極限、色々な極限(9)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{III} 色々な極限(9)\\
\lim_{x \to 0}\frac{e^{2x}-e^{-x}}{x} を求めよ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{III} 色々な極限(9)\\
\lim_{x \to 0}\frac{e^{2x}-e^{-x}}{x} を求めよ。
\end{eqnarray}
14和歌山県教員採用試験(数学:3番 微分方程式)
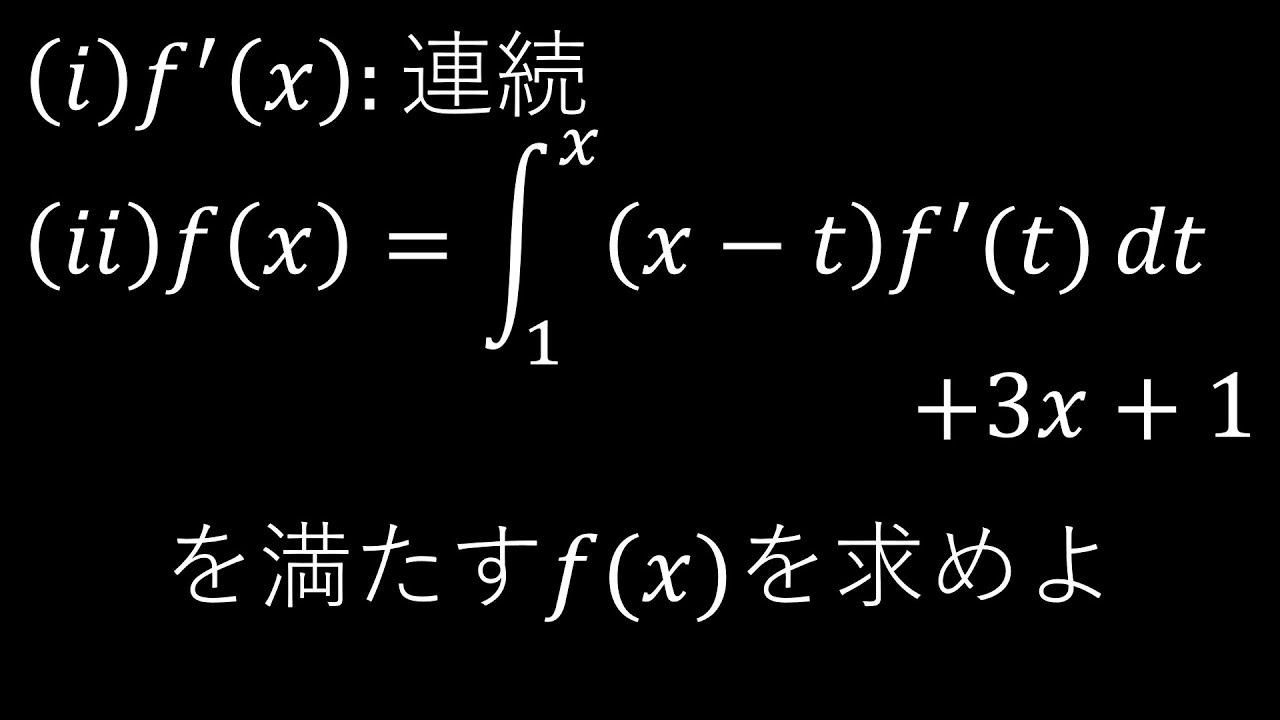
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
(i)$f`(x):$連続
(ii)$f(x)=\displaystyle \int_{1}^{x} (x-t)f`(t)dt+3x+1$
(iii)(ii)をみたす$f(x)$を求めよ.
この動画を見る
$\boxed{3}$
(i)$f`(x):$連続
(ii)$f(x)=\displaystyle \int_{1}^{x} (x-t)f`(t)dt+3x+1$
(iii)(ii)をみたす$f(x)$を求めよ.
国際数学オリンピック 積和

単元:
#積分とその応用#不定積分#定積分#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
この動画を見る
$\cos\dfrac{\pi}{7}-\cos\dfrac{2\pi}{7}+\cos\dfrac{3\pi}{7}=\dfrac{1}{2}$を示せ.
国際数学オリンピック
練習問題34 数検1級1次 微分方程式
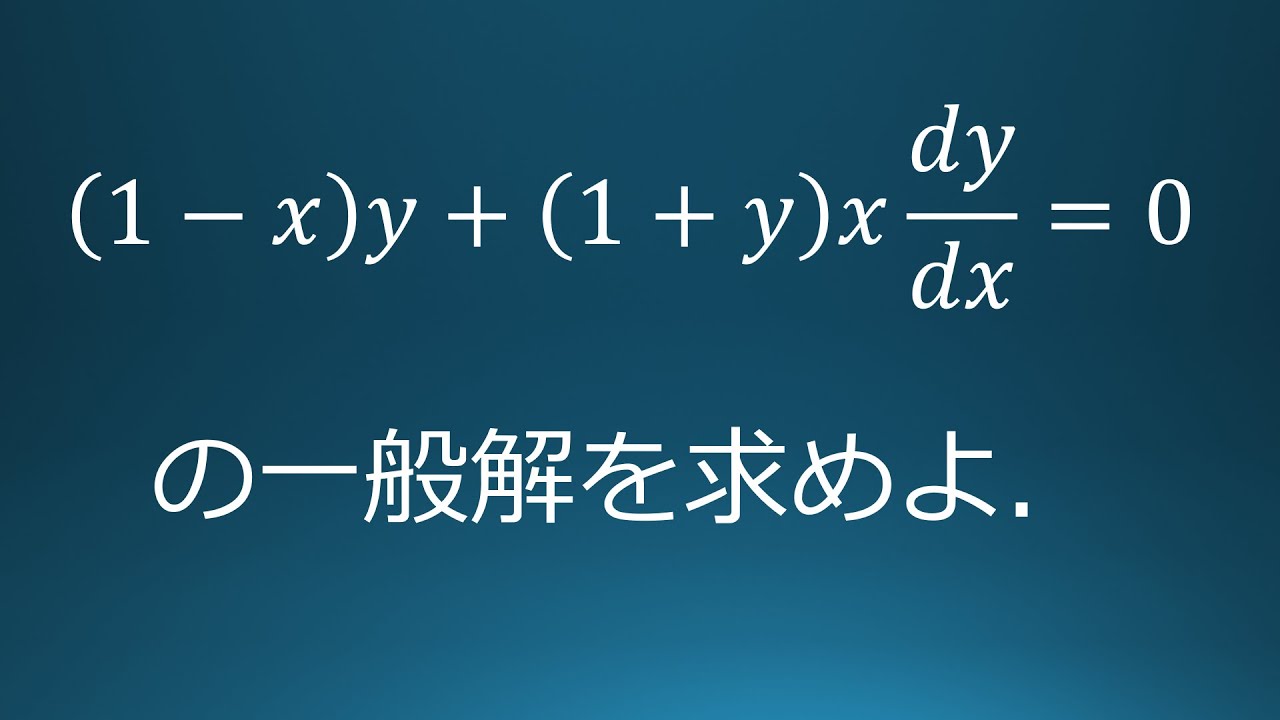
単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
この動画を見る
$(1-x)y+(1+y)x\dfrac{dy}{dx}=0$
の一般解を求めよ.
数学「大学入試良問集」【17−7 極限値が収束する条件】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知工業大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\displaystyle \lim_{ x \to \frac{\pi}{3} }\displaystyle \frac{a\ \sin\ x+b\ \cos\ x}{x-\frac{\pi}{3}}=5(a,b$は定数$)$のとき、$a$と$b$の値を求めよ。
この動画を見る
$\displaystyle \lim_{ x \to \frac{\pi}{3} }\displaystyle \frac{a\ \sin\ x+b\ \cos\ x}{x-\frac{\pi}{3}}=5(a,b$は定数$)$のとき、$a$と$b$の値を求めよ。
福田の数学〜慶應義塾大学2021年医学部第1問(2)〜回転体の体積と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
この動画を見る
${\Large\boxed{1}}$ $(2)0 \lt \alpha \lt 1,m \gt 0$とする。$曲線y=x^{\alpha}-mx(x \geqq 0)$と$x軸$で囲まれた図形を$x軸$の周りに1回転させてできる回転体の体積を$V$とする。$m$を固定して$a \to +0$とするときの$V$の極限値を$m$の式で表すと、$\lim_{a \to +0}V=\boxed{\ \ (え)\ \ }$となる。
また、$\alpha$を固定して$m \to \infty$とするとき$m^3V$が$0$でない数に収束するならば
$\alpha=\boxed{\ \ (お)\ \ }$である。
2021慶應義塾大学医学部過去問
福田のわかった数学〜高校3年生理系038〜極限(38)関数の極限、色々な極限(8)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$数学\textrm{III}$ 色々な極限(8)
$\lim_{n \to \infty}x^{2-5\alpha} (0 \lt \alpha \lt 1)$ を求めよ。
この動画を見る
$数学\textrm{III}$ 色々な極限(8)
$\lim_{n \to \infty}x^{2-5\alpha} (0 \lt \alpha \lt 1)$ を求めよ。
数学「大学入試良問集」【17−6 直線上の点の極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$f(x)=-\displaystyle \frac{1}{2}x+3$とする。
$x_1=1$とおいて数列$x_n=f(x_{n-1})$ $n=2,3,・・・$をつくり、平面座標上に点$P_n(x_n,f(x_n))$をとる。
このとき、次の各問いに答えよ。
(1)
数列$\{x_n\}$の一般項$x_n$を求めよ。
(2)
動点$P$が点$P_1$を出発して、$P_2,P_3,・・・,P_n,・・・$と進むとき、動点$P$はどのような点に近づくか。
その座標を求めよ。
(3)
線分$P_nP_{n+1}$の長さを$l_n$ $n=1,2,3,・・・$とする。
$L=\displaystyle \sum_{n=1}^n l_n$を求めよ。
この動画を見る
$f(x)=-\displaystyle \frac{1}{2}x+3$とする。
$x_1=1$とおいて数列$x_n=f(x_{n-1})$ $n=2,3,・・・$をつくり、平面座標上に点$P_n(x_n,f(x_n))$をとる。
このとき、次の各問いに答えよ。
(1)
数列$\{x_n\}$の一般項$x_n$を求めよ。
(2)
動点$P$が点$P_1$を出発して、$P_2,P_3,・・・,P_n,・・・$と進むとき、動点$P$はどのような点に近づくか。
その座標を求めよ。
(3)
線分$P_nP_{n+1}$の長さを$l_n$ $n=1,2,3,・・・$とする。
$L=\displaystyle \sum_{n=1}^n l_n$を求めよ。
数学「大学入試良問集」【17−5 図形と三角関数の極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#福島県立医科大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$O$を原点とする座標平面上に2点$A(2,0),B(0,1)$がある。
自然数$n$に対し、線分$AB$を$1:n$に内分する点を$P_n$とし、$\angle AOP_n\theta_n$とする。
ただし、$0 \lt \theta_n \lt \displaystyle \frac{\pi}{2}$である。
線分$AP_n$の長さを$l_n$として、$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{l_n}{\theta_n}$を求めよ。
この動画を見る
$O$を原点とする座標平面上に2点$A(2,0),B(0,1)$がある。
自然数$n$に対し、線分$AB$を$1:n$に内分する点を$P_n$とし、$\angle AOP_n\theta_n$とする。
ただし、$0 \lt \theta_n \lt \displaystyle \frac{\pi}{2}$である。
線分$AP_n$の長さを$l_n$として、$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{l_n}{\theta_n}$を求めよ。
福田のわかった数学〜高校3年生理系037〜極限(37)関数の極限、色々な極限(7)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$数学\textrm{III}$ $色々な極限(7)$
$\lim_{n \to \infty}n^2(\cos\frac{1}{n+1}-\cos\frac{1}{2n})$を求めよ。
この動画を見る
$数学\textrm{III}$ $色々な極限(7)$
$\lim_{n \to \infty}n^2(\cos\frac{1}{n+1}-\cos\frac{1}{2n})$を求めよ。
数学「大学入試良問集」【17−4 漸化式と等比数列・極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京農工大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
この動画を見る
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
福田のわかった数学〜高校3年生理系036〜極限(36)関数の極限、色々な極限(6)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 色々な極限(6)
$\displaystyle \lim_{x \to 0}(\frac{e^x+1}{2})^{\frac{1}{x}}$を2通りの方法で求めよ。
この動画を見る
数学$\textrm{III}$ 色々な極限(6)
$\displaystyle \lim_{x \to 0}(\frac{e^x+1}{2})^{\frac{1}{x}}$を2通りの方法で求めよ。
数学「大学入試良問集」【17−3② 解けない漸化式とはさみうちの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}=\displaystyle \frac{4a_n^2+9}{8a_n}(n=1,2,3,・・・)$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \displaystyle \frac{3}{2}(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\displaystyle \frac{3}{2} \lt \displaystyle \frac{1}{3}\left[ a_n-\dfrac{ 3 }{ 2 } \right]^2(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
この動画を見る
$a_1=2,a_{n+1}=\displaystyle \frac{4a_n^2+9}{8a_n}(n=1,2,3,・・・)$で定義される数列$\{a_n\}$について以下の問いに答えよ。
(1)$a_n \gt \displaystyle \frac{3}{2}(n=1,2,3,・・・)$を証明せよ。
(2)$a_{n+1}-\displaystyle \frac{3}{2} \lt \displaystyle \frac{1}{3}\left[ a_n-\dfrac{ 3 }{ 2 } \right]^2(n=1,2,3,・・・)$を証明せよ。
(3)$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
