 約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
 約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
良問だぜ!自画自賛
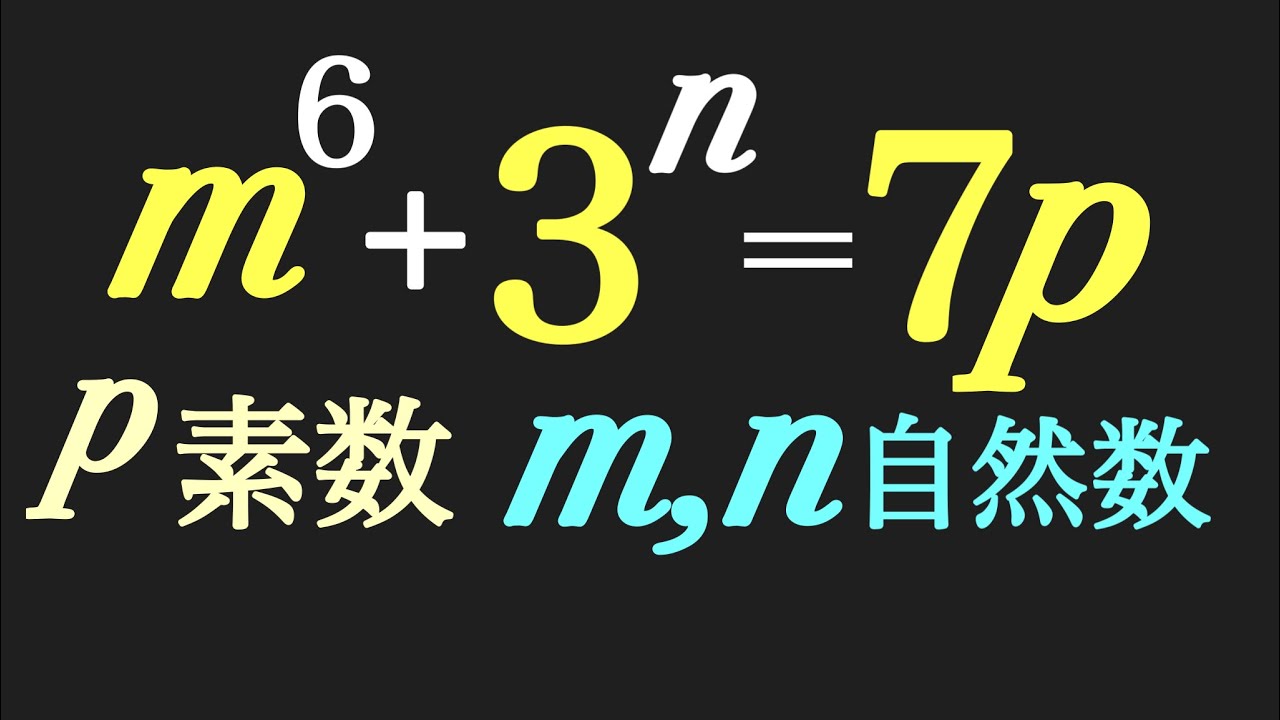
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数であり,$P$は素数である.
$m^6+3^n=7P$
これを解け.
この動画を見る
$m,n$は自然数であり,$P$は素数である.
$m^6+3^n=7P$
これを解け.
九州大の過去問をパクって問題作ってみた

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
この動画を見る
$a^3+3b^3=7c^3$を満たす整数$(a,b,c)$の組をすべて求めよ.
連続する五つの整数から一つ除く

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
この動画を見る
連続する5つの整数がある。そのうち1つを除いた4つの整数の和は2017となる。
除いた数を求めよ。
明治大学付属明治高等学校
いい問題
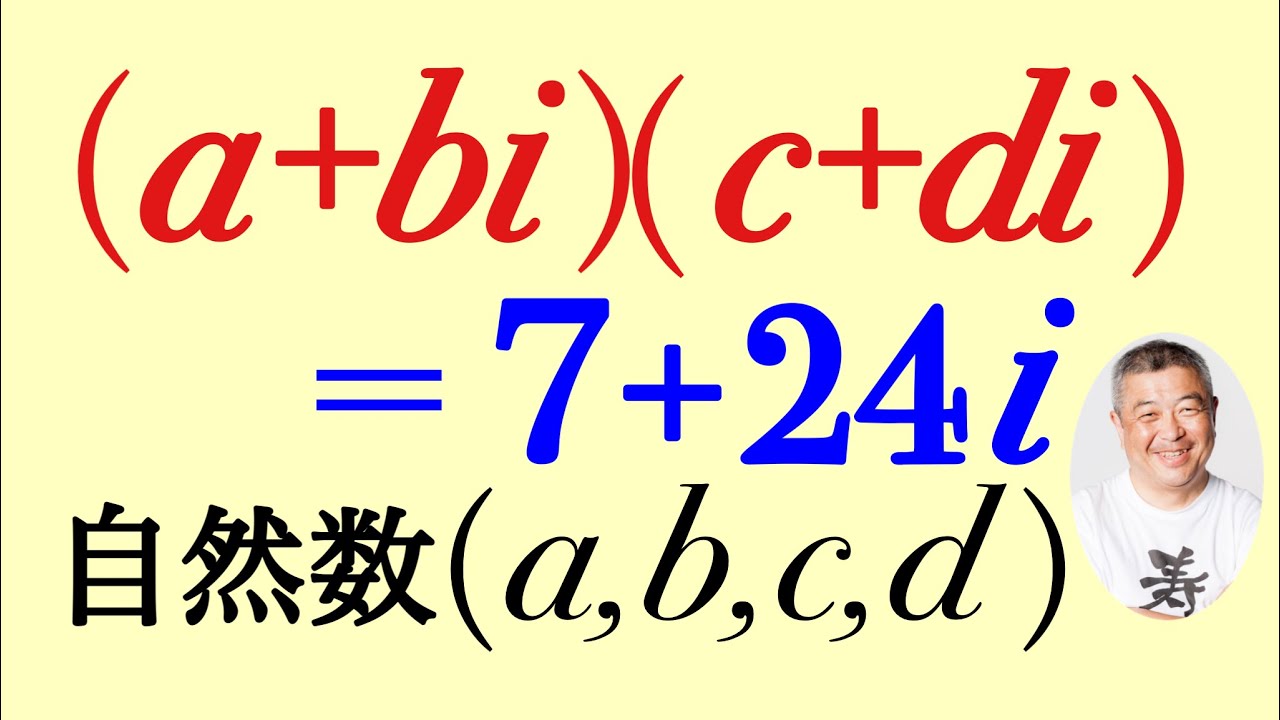
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
この動画を見る
自然数$(a,b,c,d)$をすべて求めよ.
$(a+bi)(c+di)=7+24i$
ウィルソンの定理

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
この動画を見る
$22!$を$23$で割った余りを求めよ.
$100!$を$101$で割った余りを求めよ.
整数問題
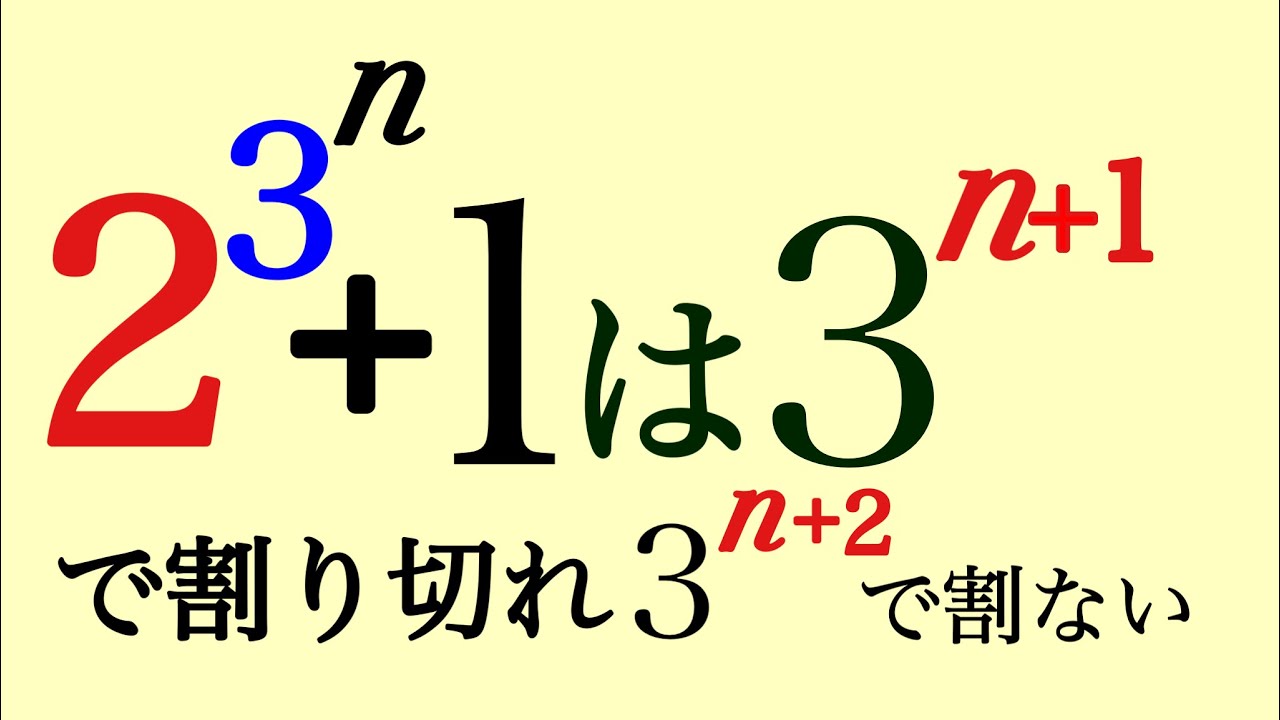
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
この動画を見る
$n$は自然数とする.
$2^{3^n}+1$は$3^{n+1}$で割り切れ,$3^{n+2}$では割り切れないことを示せ.
高校入試ではめずらしい整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^2+n$が100の倍数となる最も小さい自然数nは?
熊本マリスト学園高等学校
この動画を見る
$n^2+n$が100の倍数となる最も小さい自然数nは?
熊本マリスト学園高等学校
福田の数学〜明治大学2021年理工学部第1問(1)〜2次方程式が整数を解にもつ条件

単元:
#数Ⅰ#数A#数Ⅱ#2次関数#複素数と方程式#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
早稲田高等学院 整数 数字がない!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y = m \\
xy = n \\
x>y\\
m,nは素数
\end{array}
\right.
\end{eqnarray}
$
自然数x,y,m,nを求めよ
早稲田大学高等学院
油断禁物!!整数問題 大阪星光学院

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-28x+160$が素数となる整数xを求めよ。
この動画を見る
$x^2-28x+160$が素数となる整数xを求めよ。
整数問題2022 Σ10^10^k mod7
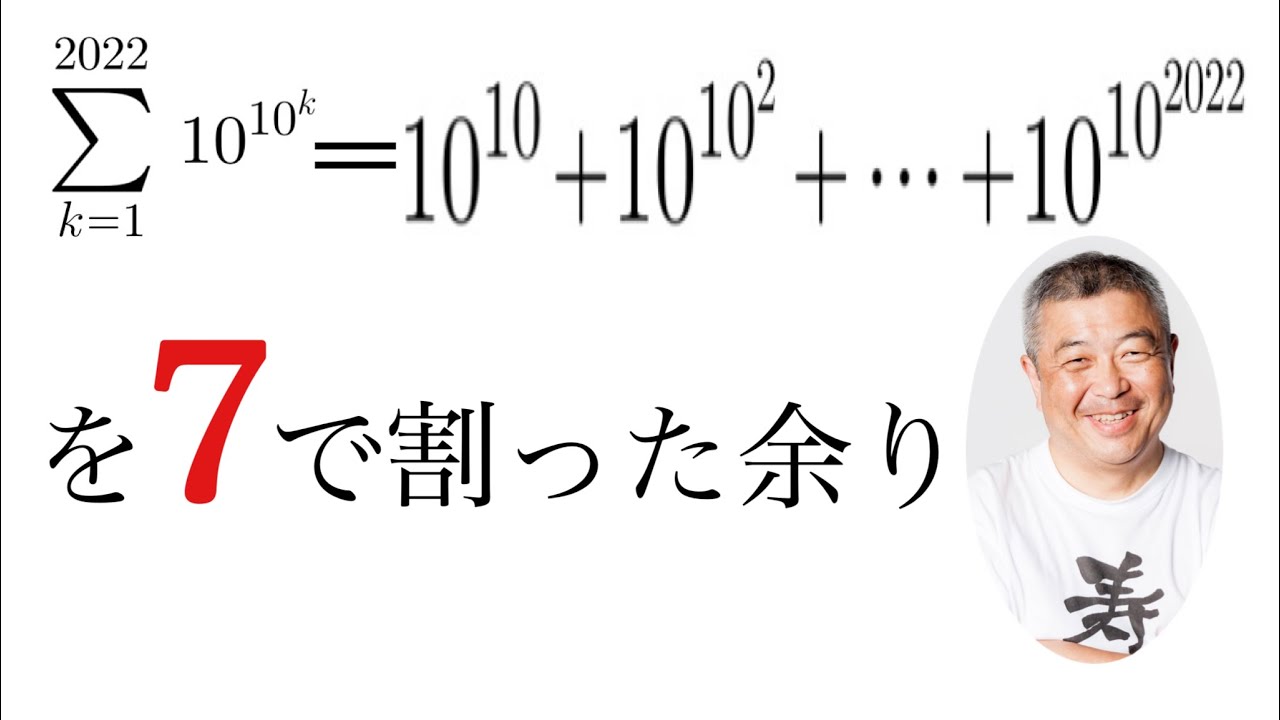
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{2022}10^{10^k}=10^{10}+10^{10^2}+・・・・・・+10^{10^{2022}}$を$7$で割った余りを求めよ.
この動画を見る
$\displaystyle \sum_{k=1}^{2022}10^{10^k}=10^{10}+10^{10^2}+・・・・・・+10^{10^{2022}}$を$7$で割った余りを求めよ.
慶應女子高校 整数問題 慶應大学理工学部の過去問!

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
平方の和で表せる2つの数の積は平方の和で表せることを証明せよ.
1962慶応理工過去問
この動画を見る
平方の和で表せる2つの数の積は平方の和で表せることを証明せよ.
1962慶応理工過去問
一橋大(類)整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^n+1$が7の倍数となる自然数$n$をすべて求めよ.
ただし,$n\leqq 50$である.
一橋大(類)過去問
この動画を見る
$n^n+1$が7の倍数となる自然数$n$をすべて求めよ.
ただし,$n\leqq 50$である.
一橋大(類)過去問
【数Ⅱ】中高一貫校問題集3(論理・確率編)124:式と証明:二項定理:21¹⁰を400で割った余りを求めよ。

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
21¹⁰を400で割った余りを求めよ。
この動画を見る
21¹⁰を400で割った余りを求めよ。
福田の数学〜上智大学2021年TEAP利用文系第4問(1)〜条件の否定

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
この動画を見る
${\Large\boxed{4}}$(1)関数$f(x)$に対する以下の条件(P)を考える。
$(P): f(x) \gt 3$を満たす5以上の自然数nが存在する。
条件(P)の否定として正しいものを以下の選択肢からすべて選べ。
$(\textrm{a})f(n) \leqq 3$を満たす5以上の自然数nが存在する。
$(\textrm{b})f(n) \gt 3$を満たす5未満の自然数nが存在する。
$(\textrm{c})f(n) \leqq 3$を満たす5未満の自然数nが存在する。
$(\textrm{d})n$が5以上の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{e})n$が5未満の自然数ならば$f(n) \leqq 3$が成り立つ。
$(\textrm{f})n$が5未満の自然数ならば$f(n) \gt 3$が成り立つ。
$(\textrm{g})f(n) \gt 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{h})f(n) \leqq 3$が5以上の全ての自然数nに対して成り立つ。
$(\textrm{i})f(n) \leqq 3$が5未満の全ての自然数nに対して成り立つ。
2021上智大学文系過去問
大阪桐蔭 整数問題 定番

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1~50のすべての整数をかけた数は5で何回まで割り切れるか?
大阪桐蔭高等学校
この動画を見る
1~50のすべての整数をかけた数は5で何回まで割り切れるか?
大阪桐蔭高等学校
福田の数学〜中央大学2021年理工学部第3問〜剰余類による分類

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$自然数$a$を3で割った余りを$r(r=0,1,2)$とする.以下の問いに答えよ.
(1)以下を求めよ.
(ア)$r=0$のとき,$a^3+4$を3で割った余り
(イ)$r=1$のとき,$a^3+4$を3で割った余り
(ウ)$r=2$のとき,$a^3+4$を3で割った余り
(2)3つの自然数$a,a^3+4,a^5+8$のうちいずれか1つは3の倍数であることを示せ.
(3)3つの自然数$a,a^3+4,a^5+8$が同時に素数となる$a$をすべて求めよ.
2021中央大理工学部過去問
この動画を見る
$\boxed{3}$自然数$a$を3で割った余りを$r(r=0,1,2)$とする.以下の問いに答えよ.
(1)以下を求めよ.
(ア)$r=0$のとき,$a^3+4$を3で割った余り
(イ)$r=1$のとき,$a^3+4$を3で割った余り
(ウ)$r=2$のとき,$a^3+4$を3で割った余り
(2)3つの自然数$a,a^3+4,a^5+8$のうちいずれか1つは3の倍数であることを示せ.
(3)3つの自然数$a,a^3+4,a^5+8$が同時に素数となる$a$をすべて求めよ.
2021中央大理工学部過去問
整数問題だよ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m^2+1232=3^n$を満たす自然数$(m,n)$をすべて求めよ.
この動画を見る
$m^2+1232=3^n$を満たす自然数$(m,n)$をすべて求めよ.
整数問題 華麗な論法

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2021m+1=7^n$を満たす自然数$m,n$が存在することを示せ.
この動画を見る
$2021m+1=7^n$を満たす自然数$m,n$が存在することを示せ.
兵庫県立大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$48n+3=m^2$を満たす整数$(m,n)$は存在しないことを示せ.
2021兵庫県立大過去問
この動画を見る
$48n+3=m^2$を満たす整数$(m,n)$は存在しないことを示せ.
2021兵庫県立大過去問
福田の数学〜慶應義塾大学2021年看護医療学部第1問(5)〜約数の個数が6個の自然数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (5)自然数nは1とn以外にちょうど4個の約数をもつとする。このような
自然数nの中で、最小の数は$\boxed{\ \ ク\ \ }$であり、最小の奇数は$\boxed{\ \ ケ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (5)自然数nは1とn以外にちょうど4個の約数をもつとする。このような
自然数nの中で、最小の数は$\boxed{\ \ ク\ \ }$であり、最小の奇数は$\boxed{\ \ ケ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
123123‥‥123の中には2021の倍数が必ずある

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$123123・・・・・・123$のように$123$が繰り返し並ぶ数の中には必ず$2021$の倍数があることを示せ.
この動画を見る
$123123・・・・・・123$のように$123$が繰り返し並ぶ数の中には必ず$2021$の倍数があることを示せ.
高校入試 数学 名古屋高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1から30までの自然数の中で6との最大公約数が1となる数は何コ?
名古屋高等学校
この動画を見る
1から30までの自然数の中で6との最大公約数が1となる数は何コ?
名古屋高等学校
華麗な別解

合同式の基本

高校入試 整数問題 大阪星光学院

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x+3y+6z=30を満たす自然数(x,y,z)の組は▢組ある
大阪星光学院高等学校
この動画を見る
x+3y+6z=30を満たす自然数(x,y,z)の組は▢組ある
大阪星光学院高等学校
明治学院大 整数その2

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{10^{130}}{13}$の小数第1位を求めよ.
$\dfrac{1}{13\times 10^{31}}$の小数第100位を求めよ.
2021明治学院大過去問
この動画を見る
$\dfrac{10^{130}}{13}$の小数第1位を求めよ.
$\dfrac{1}{13\times 10^{31}}$の小数第100位を求めよ.
2021明治学院大過去問
明治学院大 整数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{10^{130}}{13}$の小数第一位を求めよ.
2021明治学院大過去問
この動画を見る
$\dfrac{10^{130}}{13}$の小数第一位を求めよ.
2021明治学院大過去問
【数A】整数の性質:日本医科大学 不等式で絞る

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)5つの実数の総和が1であるならば、これらのうち少なくとも1つは$\dfrac{1}{5}$以上で あることを証明しよう。
(2)(1)の結果を利用して、$x_1+x_2+x_3+x_4+x_5=x_1・x_2・x_3・ x_4・x_5$を満たす正の整数$x_1,x_2,x_3,x_4,x_5$(ただし、 $x_1≦x_2≦x_3≦x_4≦x_5$)の組をすべて求めよう。
この動画を見る
(1)5つの実数の総和が1であるならば、これらのうち少なくとも1つは$\dfrac{1}{5}$以上で あることを証明しよう。
(2)(1)の結果を利用して、$x_1+x_2+x_3+x_4+x_5=x_1・x_2・x_3・ x_4・x_5$を満たす正の整数$x_1,x_2,x_3,x_4,x_5$(ただし、 $x_1≦x_2≦x_3≦x_4≦x_5$)の組をすべて求めよう。
負の数の商と余り

