 微分法
微分法
 微分法
微分法
福田の数学〜早稲田大学2022年理工学部第5問〜対数関数の極限と変曲点とグラフの接線

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
福田の数学〜九州大学2022年理系第5問の背景を考える〜内サイクロイド曲線(ハイポサイクロイド、アステロイド)の媒介変数表示

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上の曲線#ベクトルと平面図形、ベクトル方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第5問〜媒介変数表示のグラフの対称性とグラフの追跡

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
大学入試問題#153 東京医科大学(2017) 微積の応用

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
2022藤田医科大の簡単な問題 メインはn個の相加相乗平均の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
この動画を見る
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
2^π VS π^2 どっちがでかい?

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$2^{\pi}$ VS $\pi^2$
ただし,$3.14\lt \pi\lt \dfrac{22}{7}$
$2.7\lt e\lt 2.8$であるとする.
この動画を見る
どちらが大きいか?
$2^{\pi}$ VS $\pi^2$
ただし,$3.14\lt \pi\lt \dfrac{22}{7}$
$2.7\lt e\lt 2.8$であるとする.
福田の数学〜東京慈恵会医科大学2022年医学部第2問〜微分可能性と最大値と体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
福田のわかった数学〜高校3年生理系108〜変化率(3)水の問題(2)

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 変化率(3) 水の問題(2)
右図(※動画参照)のような直円錐の容器に水が満たされている。下側から$2cm^3$秒
の割合で水が流出する。水面の高さが8cmになった瞬間の水面の下降する
速度と水面の面積が減少する速度を求めよ。
この動画を見る
数学$\textrm{III}$ 変化率(3) 水の問題(2)
右図(※動画参照)のような直円錐の容器に水が満たされている。下側から$2cm^3$秒
の割合で水が流出する。水面の高さが8cmになった瞬間の水面の下降する
速度と水面の面積が減少する速度を求めよ。
福田のわかった数学〜高校3年生理系105〜絶対不等式(3)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(3)
$0 \leqq x \lt \frac{\pi}{2}$であるすべてのxについて
$\sin x\cos x \leqq kk(\sin^2x+3\cos^2x)$
が成り立つような実数kの最小値を求めよ。
福田のわかった数学〜高校3年生理系104〜絶対不等式(2)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(2)
$\sqrt x+\sqrt y \leqq k\sqrt{2x+y}$
が任意の正の実数x,yに対して成り立つような実数$k$
の値の範囲を求めよ。
福田のわかった数学〜高校3年生理系103〜絶対不等式(1)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 絶対不等式(1)
$a^x \geqq x$
が任意の正の実数xに対して成り立つような
正の定数aの値の範囲を求めよ。
この動画を見る
数学$\textrm{III}$ 絶対不等式(1)
$a^x \geqq x$
が任意の正の実数xに対して成り立つような
正の定数aの値の範囲を求めよ。
福田のわかった数学〜高校3年生理系102〜大小比較(2)
単元:
#微分とその応用#微分法#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
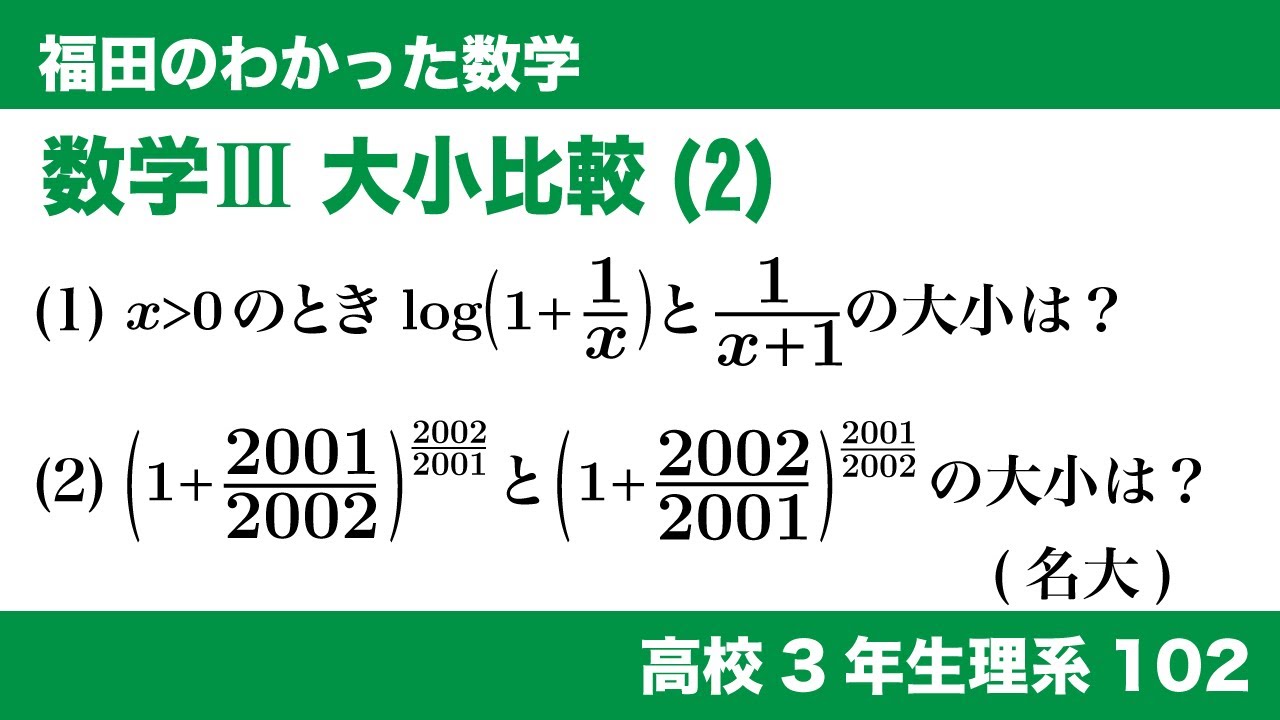
数学$\textrm{III}$ 大小比較(2)
(1)$x \gt 0$のとき$\log(1+\frac{1}{x})と\frac{1}{x+1}$の大小を比較せよ。
(2)$(1+\frac{2001}{2002})^{\frac{2002}{2001}}と(1+\frac{2002}{2001})^{\frac{2001}{2002}}$の大小を比較せよ。
この動画を見る
数学$\textrm{III}$ 大小比較(2)
(1)$x \gt 0$のとき$\log(1+\frac{1}{x})と\frac{1}{x+1}$の大小を比較せよ。
(2)$(1+\frac{2001}{2002})^{\frac{2002}{2001}}と(1+\frac{2002}{2001})^{\frac{2001}{2002}}$の大小を比較せよ。
福田のわかった数学〜高校3年生理系101〜大小比較(1)

単元:
#数Ⅱ#指数関数と対数関数#指数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$textrm{III}$大小比較(1)$999^{1000}$と$1000^{999}$
の大小を比較せよ。
この動画を見る
数学$textrm{III}$大小比較(1)$999^{1000}$と$1000^{999}$
の大小を比較せよ。
福田のわかった数学〜高校3年生理系100〜不等式の証明(7)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(7)
$e^a(b-a) \lt e^b-e^a \lt e^b(b-a)$
(ただし、$a \lt b$)
この動画を見る
数学$\textrm{III}$ 不等式の証明(7)
$e^a(b-a) \lt e^b-e^a \lt e^b(b-a)$
(ただし、$a \lt b$)
福田のわかった数学〜高校3年生理系099〜不等式の証明(6)
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
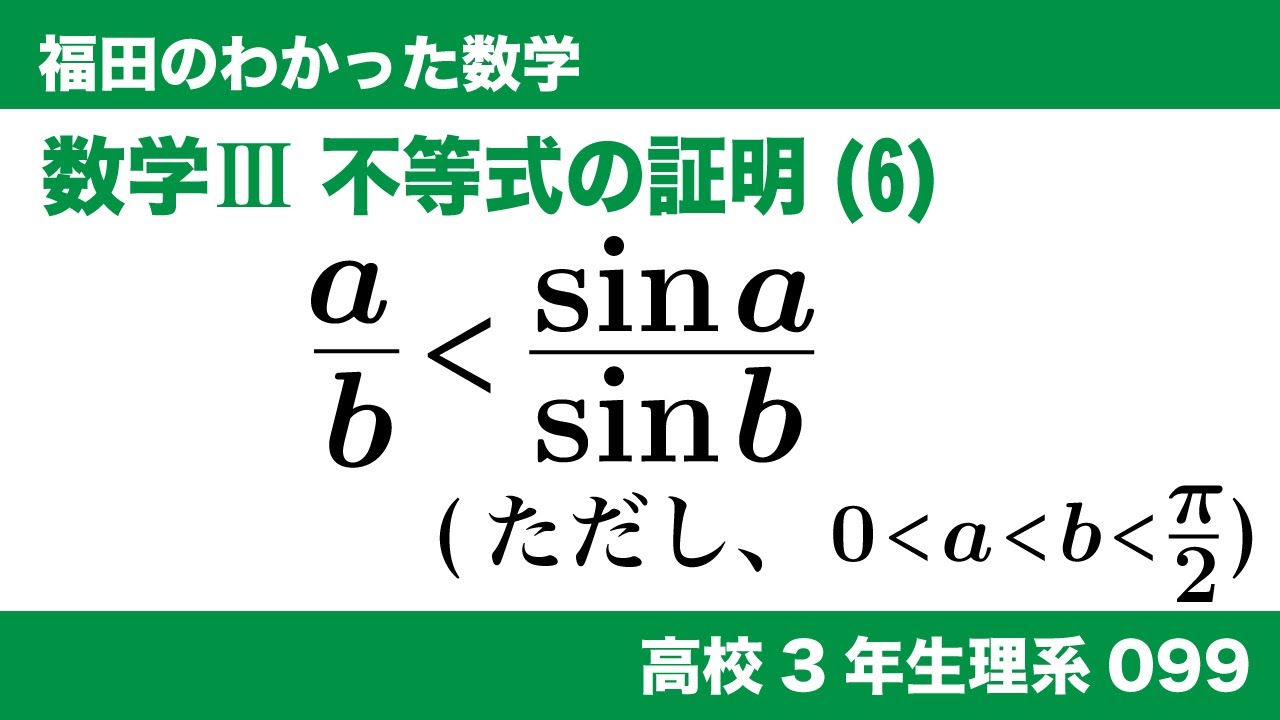
数学$\textrm{III}$ 不等式の証明(6)
$0 \lt a \lt b \lt \frac{\pi}{2}$のとき、
$\frac{a}{b} \lt \frac{\sin a}{\sin b}$が成り立つことを証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(6)
$0 \lt a \lt b \lt \frac{\pi}{2}$のとき、
$\frac{a}{b} \lt \frac{\sin a}{\sin b}$が成り立つことを証明せよ。
福田のわかった数学〜高校3年生理系098〜不等式の証明(5)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
福田のわかった数学〜高校3年生理系097〜不等式の証明(4)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
福田のわかった数学〜高校3年生理系096〜不等式の証明(3)
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
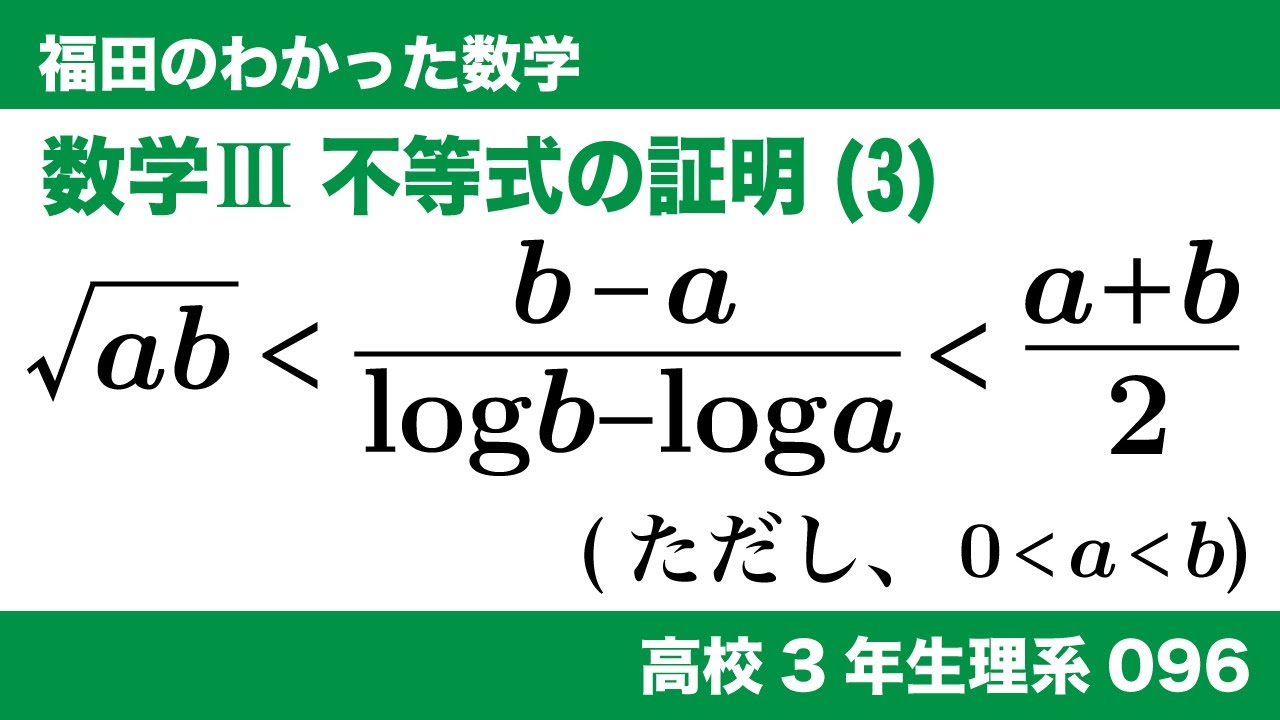
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
福田のわかった数学〜高校3年生理系095〜不等式の証明(2)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(2)
$x\log x \geqq (x-1)\log(x+1) (x \geqq 1)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(2)
$x\log x \geqq (x-1)\log(x+1) (x \geqq 1)$を証明せよ。
福田のわかった数学〜高校3年生理系094〜不等式の証明(1)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(1)
$\cos x \lt 1-\frac{x^2}{2}+\frac{x^4}{24} (x \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(1)
$\cos x \lt 1-\frac{x^2}{2}+\frac{x^4}{24} (x \gt 0)$を証明せよ。
微分方程式 高専数学 p 100(1)(2)
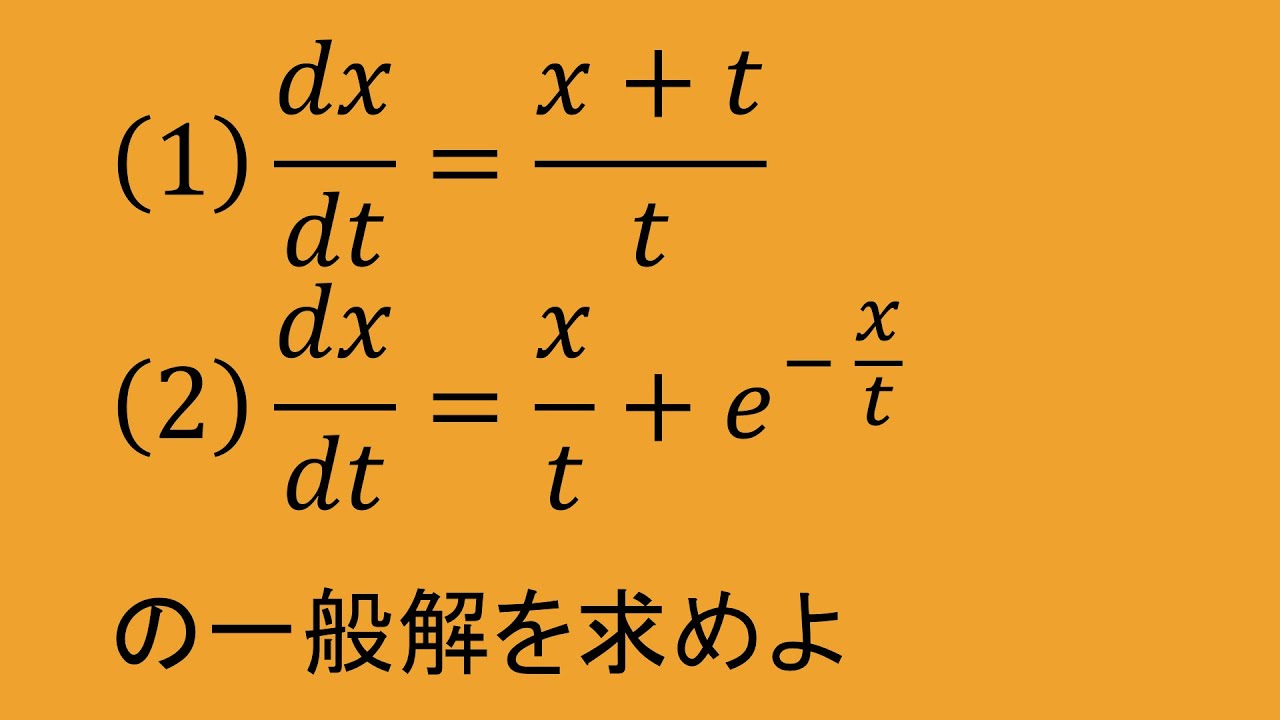
単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
微分方程式
(1)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x+t}{t}$
(2)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x}{t}+e^\frac{x}{t}$
の一般解を求めよ。
この動画を見る
微分方程式
(1)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x+t}{t}$
(2)$\displaystyle \frac{dx}{dt}=\displaystyle \frac{x}{t}+e^\frac{x}{t}$
の一般解を求めよ。
微分方程式 高専数学 p 106-1番

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
微分方程式
$\displaystyle \frac{dx}{dt}=\sqrt{ 2t+x+4 }$の一般解を求めよ。
この動画を見る
微分方程式
$\displaystyle \frac{dx}{dt}=\sqrt{ 2t+x+4 }$の一般解を求めよ。
09高知県教員採用試験(数学:1-(5) 微分方程式)
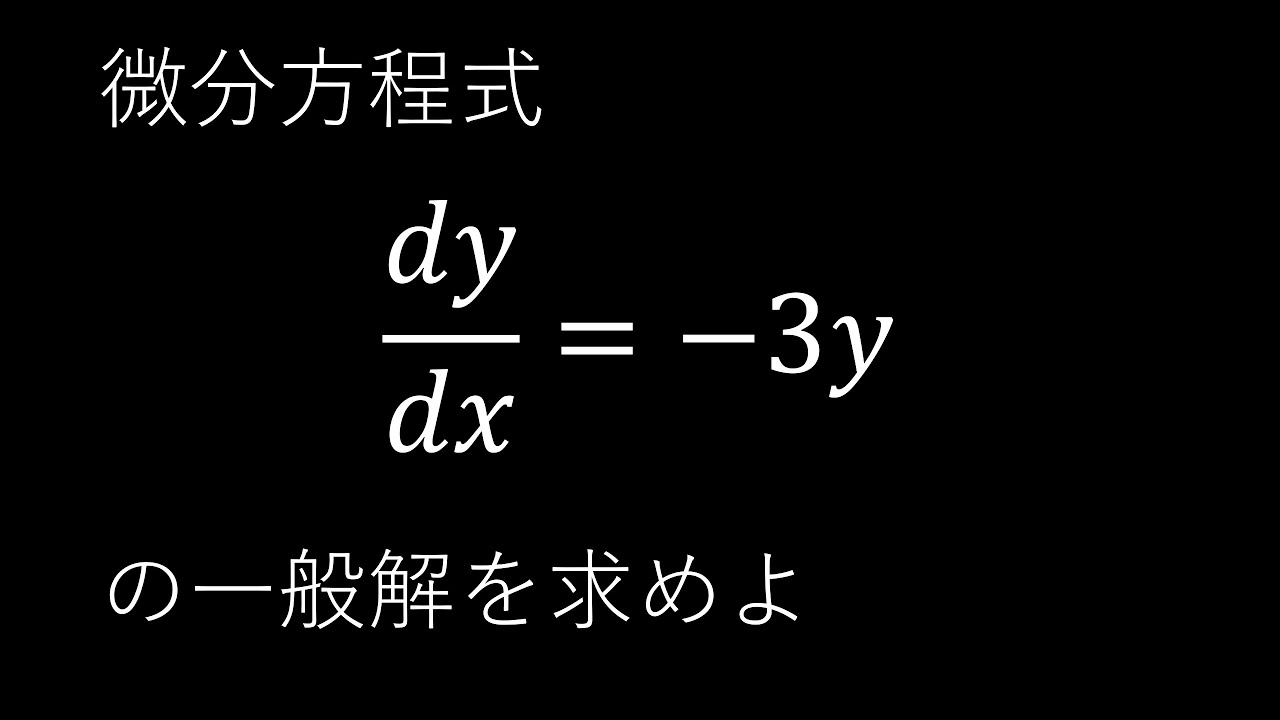
福田のわかった数学〜高校3年生理系081〜グラフを描こう(3)対数関数のグラフ

単元:
#数Ⅱ#指数関数と対数関数#対数関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(3)
$y=x(\log x-1)^2$
のグラフを描け。ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(3)
$y=x(\log x-1)^2$
のグラフを描け。ただし凹凸は調べなくてよい。
x^πを微分せよ

福田の数学〜明治大学2021年理工学部第3問〜単位ベクトルと関数の増減

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
福田のわかった数学〜高校3年生理系079〜グラフを描こう(1)分数関数のグラフ

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
福田のわかった数学〜高校3年生理系078〜極値(2)極値を求める

単元:
#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(2)
$f(x)=x^2e^{-|x-a|} (a \gt 2)$の極値を求めよ。
この動画を見る
数学$\textrm{III}$ 極値(2)
$f(x)=x^2e^{-|x-a|} (a \gt 2)$の極値を求めよ。
【数Ⅲ】微分法:媒介変数で表された関数の2回微分

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
xの関数yが、$\theta$を媒介変数として、$x=\cos\theta-1、y=2\sin\theta+1$と表される時、$\dfrac{d^2y}{dx^2}$を$\theta$の関数として表そう。
この動画を見る
xの関数yが、$\theta$を媒介変数として、$x=\cos\theta-1、y=2\sin\theta+1$と表される時、$\dfrac{d^2y}{dx^2}$を$\theta$の関数として表そう。
大学入試問題#14 津田塾大学(2021) 微積の応用

単元:
#微分とその応用#積分とその応用#微分法#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \displaystyle \frac{\pi}{x}$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}\sin|x-t|dt$の最小値、最大値を求めよ。
出典:2021年津田塾大学 入試問題
この動画を見る
$0 \leqq x \leqq \displaystyle \frac{\pi}{x}$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}\sin|x-t|dt$の最小値、最大値を求めよ。
出典:2021年津田塾大学 入試問題
