ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
数列 難易度高め by Picmin3daisukiさん #Shorts
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
大学入試問題#716「文系にはきつくね？」 早稲田商学部(2015) 数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
（$i$）$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
（$ii$）$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典：2015年早稲田大学商学部 入試問題
この動画を見る
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
（$i$）$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
（$ii$）$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典：2015年早稲田大学商学部 入試問題
大学入試問題#715「このタイプ苦手」 早稲田理工系学部(2021) 整式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^4-x^2+1$
１．$x^6$を$f(x)$で割ったときの余りを求めよ
２．$x^{2021}$を$f(x)$で割ったときの余りを求めよ
３．自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典：2021年早稲田大学理工学部 入試問題
この動画を見る
$f(x)=x^4-x^2+1$
１．$x^6$を$f(x)$で割ったときの余りを求めよ
２．$x^{2021}$を$f(x)$で割ったときの余りを求めよ
３．自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典：2021年早稲田大学理工学部 入試問題
大学入試問題#714「The basic integral problem」 青山学院大(2021) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典：2021年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典：2021年青山学院大学 入試問題
大学入試問題#713「さすがに合同式を利用」 早稲田商学部(2016) 合同式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$2^{100}$を$2016$で割ったときの余りを求めよ。
出典：2016年早稲田大学商学部 入試問題
この動画を見る
$2^{100}$を$2016$で割ったときの余りを求めよ。
出典：2016年早稲田大学商学部 入試問題
数列 By Picmin3daisukiさん
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
大学入試問題#712「泥臭い解答になってしまいました」 東邦大学医学部(2012) 整式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東邦大学
指導講師：
ますただ
問題文全文(内容文)：
$x+x^{104}$を$1-x+x^2$で割ったときの余りを求めよ。
出典：2016年東邦大学医学部 入試問題
この動画を見る
$x+x^{104}$を$1-x+x^2$で割ったときの余りを求めよ。
出典：2016年東邦大学医学部 入試問題
大学入試問題#711「この問題好きすぎ（笑）」 東京理科大学(2013) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2} \sqrt[ n ]{ {}_{ 4n }P_{2n} }$
出典：2013年トウキョウ理科大学入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2} \sqrt[ n ]{ {}_{ 4n }P_{2n} }$
出典：2013年トウキョウ理科大学入試問題
大学入試問題#710「入試開始の初手この問題！！」 関西医科大学(2023)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$(a+1)(a-1)(b+1)(b-1)=4ab$ を満たす整数の組$(a,b)$をすべて求めよ。
ただし、$a \lt b$とする。
出典：2023年関西医科大学 入試問題
この動画を見る
$(a+1)(a-1)(b+1)(b-1)=4ab$ を満たす整数の組$(a,b)$をすべて求めよ。
ただし、$a \lt b$とする。
出典：2023年関西医科大学 入試問題
早稲田人間科学部2012定積分
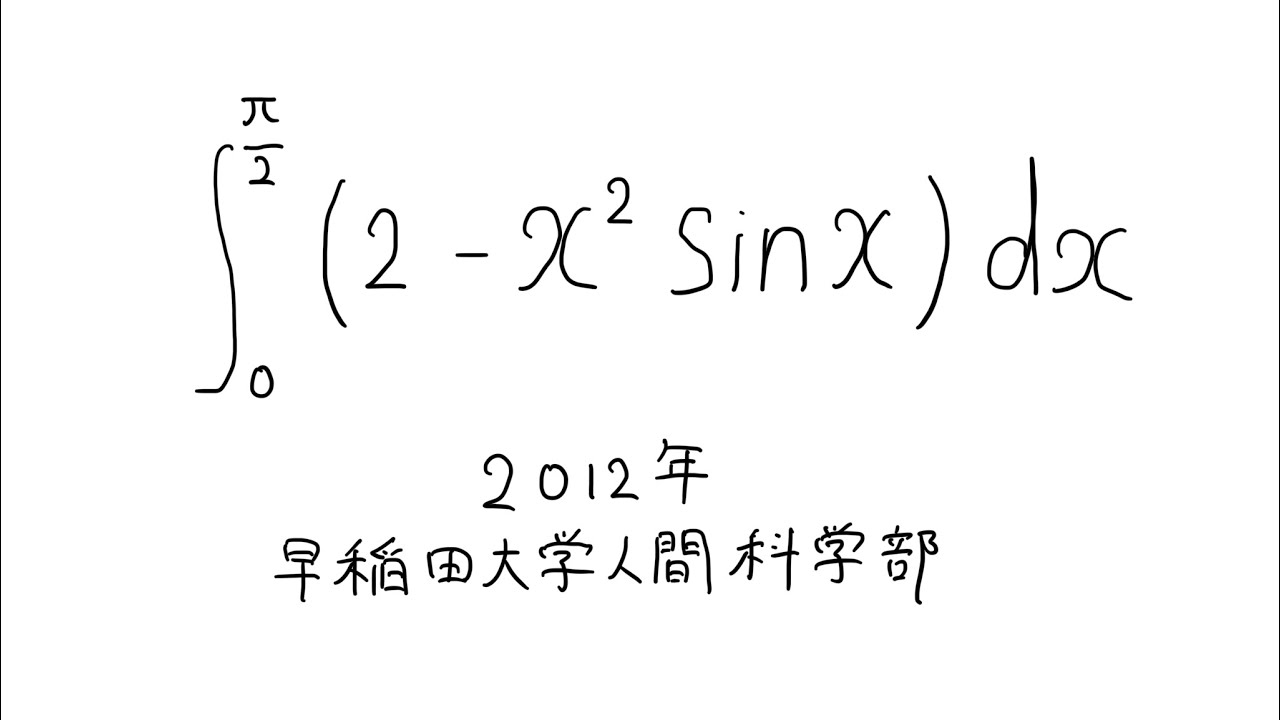
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} (2-x^2\sin\ x) dx$
出典：2012年早稲田大学人間科学部
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (2-x^2\sin\ x) dx$
出典：2012年早稲田大学人間科学部
大学入試問題#709「ちょっと大変」 東京理科大学(2012)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k,l,m,n$は自然数とする。
条件$k・l・m・n=k+l+m+n,$
$k \leq l \leq m \leq n$を満たす組$(k,l,m,n)$をすべて求めよ
出典：2012年東京理科大学 入試問題
この動画を見る
$k,l,m,n$は自然数とする。
条件$k・l・m・n=k+l+m+n,$
$k \leq l \leq m \leq n$を満たす組$(k,l,m,n)$をすべて求めよ
出典：2012年東京理科大学 入試問題
大学入試問題#708「数検1級１次でもみたことある」 東京理科大学(2013) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$
出典：2013年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\sqrt[ n ]{ {}_{ 2n } P_n }$
出典：2013年東京理科大学 入試問題
大学入試問題#707「たぶん良問だと思う」 佐賀大学(2013) 方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師：
ますただ
問題文全文(内容文)：
$x+\displaystyle \frac{1}{x}=\displaystyle \frac{y}{8}+\displaystyle \frac{8}{y}=\displaystyle \frac{x}{y}+\displaystyle \frac{y}{x}$をみたす実数$x,y$の組をすべて求めよ
出典：2013年佐賀大学 入試問題
この動画を見る
$x+\displaystyle \frac{1}{x}=\displaystyle \frac{y}{8}+\displaystyle \frac{8}{y}=\displaystyle \frac{x}{y}+\displaystyle \frac{y}{x}$をみたす実数$x,y$の組をすべて求めよ
出典：2013年佐賀大学 入試問題
大学入試問題#706 千葉大学(2014) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x)dx$
出典：2014年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x)dx$
出典：2014年千葉大学 入試問題
大学入試問題#705「時間と根性が削られる」 自治医科大学(2023)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\beta=\sqrt[ 3 ]{ 7+5\sqrt{ 2 } }$であるとき、
$\beta^4-12\beta$の値を求めよ。
出典：2023年自治医科大学 入試問題
この動画を見る
$\beta=\sqrt[ 3 ]{ 7+5\sqrt{ 2 } }$であるとき、
$\beta^4-12\beta$の値を求めよ。
出典：2023年自治医科大学 入試問題
Picmin3daisukiさんの数列（オリジナル）
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_1=\sqrt{ 3 }$
$\displaystyle \frac{a_{n+1}}{a_n}=a_{n+1}\ a_n+2$のとき一般項$a_n$を求めよ
この動画を見る
$a_1=\sqrt{ 3 }$
$\displaystyle \frac{a_{n+1}}{a_n}=a_{n+1}\ a_n+2$のとき一般項$a_n$を求めよ
大学入試問題#704 東京理科大学(2013) #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} x\ \sin\displaystyle \frac{x}{3} dx$
出典：2013年東京理科大学
この動画を見る
$\displaystyle \int_{0}^{\pi} x\ \sin\displaystyle \frac{x}{3} dx$
出典：2013年東京理科大学
大学入試問題#703「まあ落としたくない」 東京理科大学(2014) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{4} \displaystyle \frac{x}{\sqrt{ 2x+1 }} dx$
出典：2014年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{x}{\sqrt{ 2x+1 }} dx$
出典：2014年東京理科大学 入試問題
大学入試問題#702「落としたくない」 東京理科大学(2013) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{\sqrt{ x }+1} dx$
出典：2013年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{\sqrt{ x }+1} dx$
出典：2013年東京理科大学 入試問題
大学入試問題#701「ええ問題や～～～」 獨協医科大学(2012) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} x^6(1-x^2)^{\frac{5}{2}}dx$
出典：2012年獨協医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x^6(1-x^2)^{\frac{5}{2}}dx$
出典：2012年獨協医科大学 入試問題
大学入試問題#700「章末問題」 早稲田大学社会学部(2022)整式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
整式$P(x)$を
$x-1$で割ると1余り、
$(x+1)^2$で割ると$3x+2$余る。
このとき、$P(x)$を$(x-1)(x+1)^2$で割ったときの余りを求めよ
出典：2022年早稲田大学社会学部 入試問題
この動画を見る
整式$P(x)$を
$x-1$で割ると1余り、
$(x+1)^2$で割ると$3x+2$余る。
このとき、$P(x)$を$(x-1)(x+1)^2$で割ったときの余りを求めよ
出典：2022年早稲田大学社会学部 入試問題
大学入試問題#699「まあまあ基本」 早稲田大学社会学部(2023) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$xyz=x+y+z$を満たす整数$x,y,z$の組をすべて求めよ。
$(0 \lt x \leq y \leq z)$
出典：2023年早稲田大学社会学部 入試問題
この動画を見る
$xyz=x+y+z$を満たす整数$x,y,z$の組をすべて求めよ。
$(0 \lt x \leq y \leq z)$
出典：2023年早稲田大学社会学部 入試問題
大学入試問題#698「基本問題」 昭和大医学部(2005) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x-10}{x^2+x-12} dx$
出典：2005年昭和大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x-10}{x^2+x-12} dx$
出典：2005年昭和大学医学部 入試問題
大学入試問題#697「正面突破はしないよね」 早稲田人間科学部(2022)方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x(x-1)(x-2)(x-3)+1=0$の解を求めよ
出典：2014年早稲田大学人間科学部 入試問題
この動画を見る
方程式
$x(x-1)(x-2)(x-3)+1=0$の解を求めよ
出典：2014年早稲田大学人間科学部 入試問題
大学入試問題#696「基本問題だけど、良問」 久留米大学医学部(2014)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} log(\sqrt{ x }+1) dx$
出典：2014年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} log(\sqrt{ x }+1) dx$
出典：2014年久留米大学医学部 入試問題
大学入試問題#695「良き整数問題」 早稲田商学部(1999) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a,b,c$は整数の定数である。
すべての実数$x$について
$(x-a)(x-99)+2=(x-b)(x-c)$
が成り立つとき、$a,b,c$の値の組をすべて求めよ。
出典：1999年早稲田大学商学部 入試問題
この動画を見る
$a,b,c$は整数の定数である。
すべての実数$x$について
$(x-a)(x-99)+2=(x-b)(x-c)$
が成り立つとき、$a,b,c$の値の組をすべて求めよ。
出典：1999年早稲田大学商学部 入試問題
大学入試問題#694「The king property」 東京女子医科大学(2008) キングプロパティ
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京女子医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1} \displaystyle \frac{|x|}{1+e^x} dx$
出典：2008年東京女子医科大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{|x|}{1+e^x} dx$
出典：2008年東京女子医科大学 入試問題
大学入試問題#693「部分分数分解ばかり」 久留米大学医学部(2010)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#久留米大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{4}^{5} \displaystyle \frac{3x-7}{x^3-6x^2+11x-6} dx$
出典：2010年久留米大学医学部 入試問題
この動画を見る
$\displaystyle \int_{4}^{5} \displaystyle \frac{3x-7}{x^3-6x^2+11x-6} dx$
出典：2010年久留米大学医学部 入試問題
大学入試問題#692「定積分の王道」 産業医科大学(2012) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{3}^{4} \displaystyle \frac{6x+5}{x^3-3x-2} dx$
出典：2012年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{3}^{4} \displaystyle \frac{6x+5}{x^3-3x-2} dx$
出典：2012年産業医科大学 入試問題
大学入試問題#690「至高の部分分数分解」 東京女子医科大学(2014)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京女子医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2+2x+2}{x(x+1)(x+2)} dx$
出典：2017年東京女子医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{x^2+2x+2}{x(x+1)(x+2)} dx$
出典：2017年東京女子医科大学 入試問題